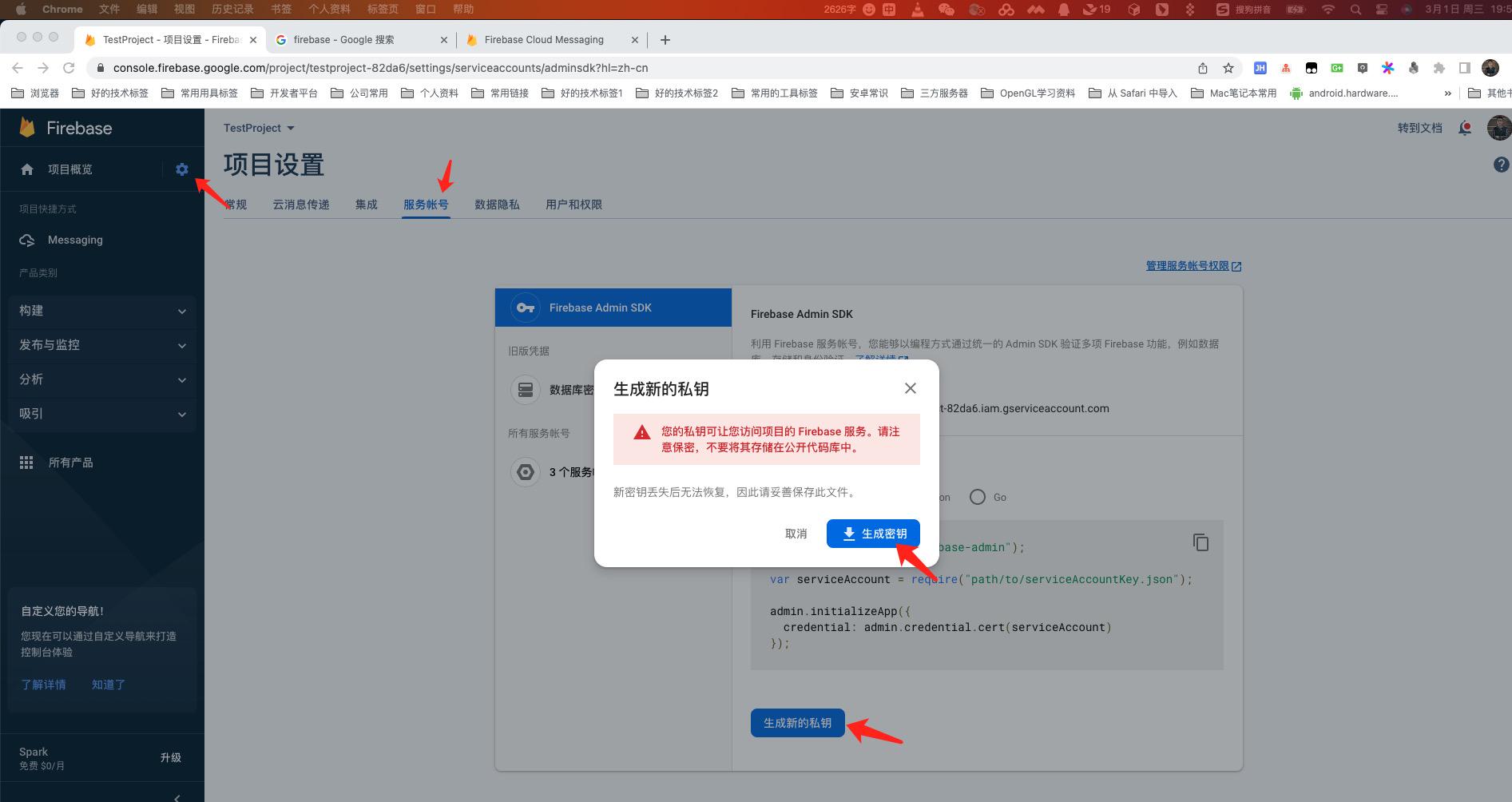
本系列文章为笔者在学习b站中科大郑烇老师的计算机网络课程时（郑老师讲得很清晰！！），结合课程PPT与《计算机网络：自顶向下方法》（第七版）所作的学习笔记，部分图片源自课程PPT或书中，如有侵权，请联系作者删除。

笔记汇总

Chapter5

• 笔记汇总
• 5.1 路由选择算法
• • 5.1.1 路由的概念
  • 5.1.2 路由选择算法
  • • 原则
    • 分类
  • 5.1.3 LS路由选择算法
  • • 大致工作流程
    • 具体细节
    • 可能的震荡问题
  • 5.1.4 距离矢量路由选择算法
  • • 主要思想
    • 特点
  • 5.1.5 LS和DV算法的比较

5.1 路由选择算法

5.1.1 路由的概念

按照某种指标，找到从源节点到目标节点的较好路径。

• 较好路径：按照某种指标，代价较小的路径
• 指标：延迟、费用、队列长度等

以网络为单位进行路由，一个网络的所有节点地址前缀相同，且物理上聚集，路由信息传输、计算和匹配的代价低。

由于到了网络中的路由器时意味着可以到达网络中的任意一台主机（由链路层解决），于是可以用路由器代表一个网络，且将路由器抽象成图上的节点，路由器与路由器之间的代价抽象成边，把路由问题当成图的最短路问题。

5.1.2 路由选择算法

原则

• 正确性：算法必须是正确和完整的
• 简单性：算法在计算机上应简单
• 健壮性：算法能够适应通信量和网络拓扑的变化
• 稳定性：产生的路由不应该摇摆
• 公平性：对每一个站点都公平
• 最优性：某个指标的最优（如果代价太高，也可以不追求最优）

分类

第一种分类方式，根据算法是集中式还是分布式的来分

• 集中式路由选择算法（全局）
  所有路由器有完整的网络拓扑结构和边的代价信息，如链路状态（Link State, LS）算法。
• 分散式路由选择算法（分布式）
  路由器只知道与它有物理连接关系的邻居路由器到它的代价信息，迭代地与邻居交换信息，计算路由信息，如距离向量（Distance-Vector, DV）算法。

第二种分类方式，根据算法是静态的还是动态的来分

• 静态路由选择算法
  路由随时间变化缓慢，人工调整。
• 动态路由选择算法
  路由变化很快，周期性更新路由信息，根据链路代价的变化而辩护。

5.1.3 LS路由选择算法

大致工作流程

各点通过各种渠道获得整个网络拓扑结构，链路代价等信息，然后使用LS路由选择算法（dijkstra算法），计算出本节点到其他所有节点的最优路径，得到路由表。

具体细节

• 发现相邻节点，获知对方地址
• 测量到相邻节点的代价
• 组装分组，描述相邻节点情况（节点名称，代价）
• 将LS分组泛洪到整个网络中（序号、AGE年龄字段用于避免重复泛洪，如果序号之前在节点中出现过，则不对外发送，如果AGE年龄字段减为0，则丢弃该分组）
• 通过LS分组获知整个网络拓扑结构和链路代价，用Dijkstra算法计算最短路（Dijkstra在这就不细讲了）

可能的震荡问题

如下图中的例子，假设链路的代价为链路实时流量，一开始x、y、z到w的路径均为顺时针方向，这会使得x到w的代价变小，在下一个计算周期时，将会把路径切换为逆时针方向，依次类推，路由将反复震荡。

图片来源于《自顶向下》

5.1.4 距离矢量路由选择算法

主要思想

距离矢量算法是一种迭代的、异步的和分布式的算法的，其基本思想是：

• 各路由器维护一张路由表
• 各路由器与相邻路由器交换路由表
  定期测量与相邻节点的代价，定期交换路由表
• 根据获得的路由信息，更新路由表
  使用Bellman-Ford方程进行更新：
  假设$d_x(y)$为从x到y的最小路径代价，则 d x ( y ) = m i n v { c ( x , v ) + d v ( y ) } d_x(y)=min_v\{c(x, v) + d_v(y)\} dx​(y)=minv​{c(x,v)+dv​(y)}，其中$v$为$x$的相邻节点

特点

• 分布式
  每个节点需要从一个或多个直接邻居获取路由信息，然后将其计算结果分发给它的邻居
• 迭代
  过程要持续到收敛为止，即所有邻居之间都没有有用信息交换
• 异步
  各节点间的计算是独立的，步伐不需要一致
• 好消息传得快
  好消息的传播以每一个交换周期前进一个路由器的速度进行（好消息指的是某个路由器接入或有更短的路径），如下图例子，当路由器A接入互联网中时，B获取其最短路径长度并向C方向扩散，一个周期一个路由器。
  

图片来源于课程PPT

• 坏消息传的慢
  无穷计算的问题，考虑下图例子，当路由器A退出互联网时，B到A的直接链路不可达，但是C向B发送的路由信息却显示可达，于是B从C更新（这显然是不对的），导致传播速度将非常缓慢。
  

图片来源于课程PPT

5.1.5 LS和DV算法的比较

• 消息复杂度（DV胜出）
  LS：有$n$个节点，$E$条链路，发送报文$O(nE)$
  DV：只和邻居交换路由信息

• 收敛时间（LS胜出）
  LS：$O(n^2)$朴素算法，$O(nlogn)$优化算法，有可能产生震荡
  DV：收敛较慢，可能存在路由环路，无穷计算问题

• 健壮性（LS胜出）
  当路由器故障时，
  LS：节点会向其邻居通告不正确的链路代价，由于每个节点只计算自己的路由表，路由计算在某种程度上是可分离的，故错误信息影响较小，较局部。
  DV：节点可以通过交换路由信息向任意或所有目标节点通告不正确的链路代价，通过邻居的邻居扩散到整个网络。