一、希尔伯特变换器（✔️ ）

1. 什么是希尔伯特变换器？

2. 试证明信号通过希尔伯特变换器后的输出

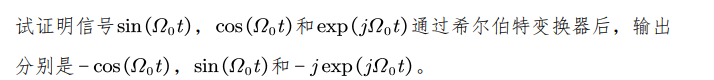
例题：

其实要点就是把 sin cos 函数的频谱 也就是傅里叶变换，再分 w>0 和 w<0 部分和 H(jw) 相乘 再化成时域函数就好啦。

---

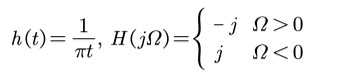
二、能量信号的自相关函数、卷积运算与能量谱（✔️）

1. 能量信号

• 能量信号
  定义：信号能量等于一个有限正值，但平均功率为零。
  特征：信号的振幅和持续时问均有限，非周期性
  实例：单个矩形脉冲
  

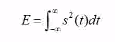
• 自相关函数
  

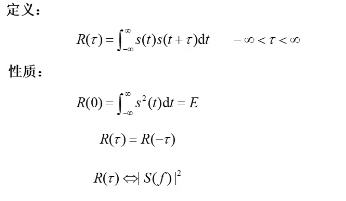
• 卷积运算
  

• 能量谱
  

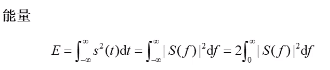
结论
能量信号在 零时刻的自相关函数 就等于 信号的能量；
自相关函数是偶函数；
能量信号的 自相关函数 与 信号能量谱密度 是 傅里叶变换对。

2. 试证明自相关函数运算与卷积运算的关系

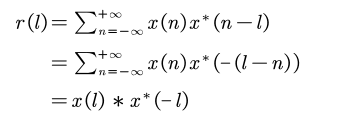
3. 试证明自相关函数的傅里叶变换是能量谱，即信号幅度谱的平方

---

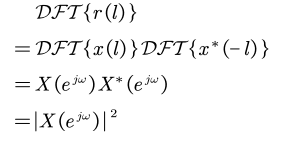
三、FIR 滤波器（✔️）

1. 相关概念

1. FIR 滤波器的冲激响应 一定是有限长的，如 h(n) = {1,2,3}，其他位置为 0
2. 显然 FIR 滤波器一定是稳定系统 （h(n) 累加和是绝对可和的）
3. FIR 为全0点系统
4. 若要求 FIR 滤波器是线性相位 FIR 滤波器，那么 必须满足对称性
   
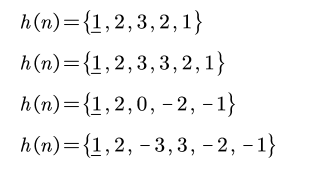
5. 会画线性相位 FIR 滤波器的直接结构 和高效结构 h(n) = {1,2,3,2,1}
   

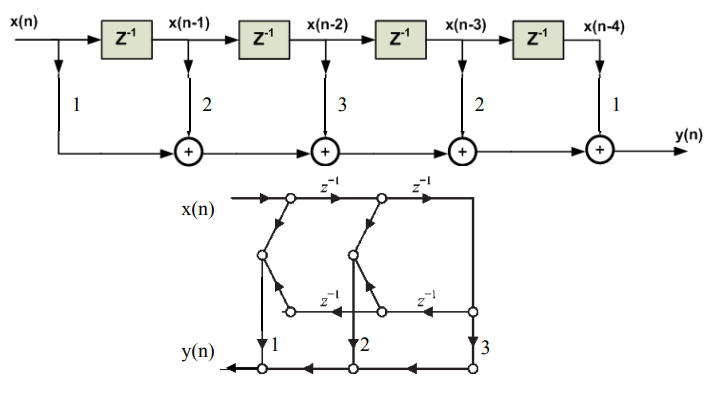
2. 重要结论

1. 如果 z₀ 是线性相位FIR滤波器的零点，那么 Z^*,1 / Z₀，1/Z₀^* 都是线性相位FIR滤波器的零点。
2. 当线性相位FIR滤波器的零点个数为单数时，如果滤波器是高通滤波器，那么在 z=+1处存在零点；如果滤波器是低通滤波器，那么在 z =-1 处存在零点。

---

四、DFT 与 FFT（✔️）

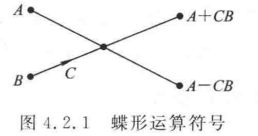
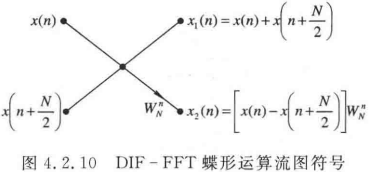
1. 画 4 点基 2-DIT（时域抽取）-FFT 和基 2-DIF（频域抽取）-FFT 流图

公共运算：

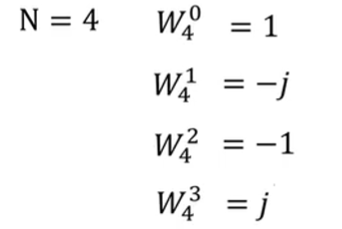
• DIF-FFT
  
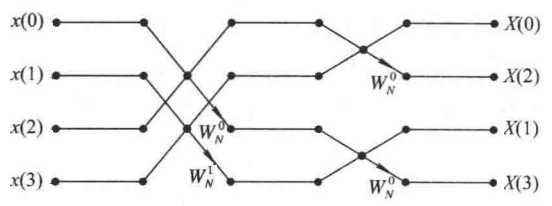
• DIT-FFT
  

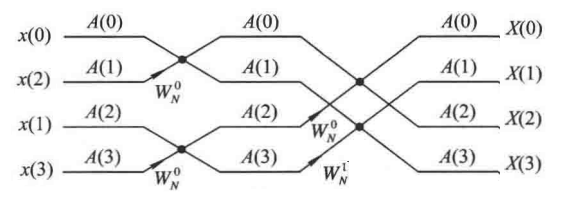
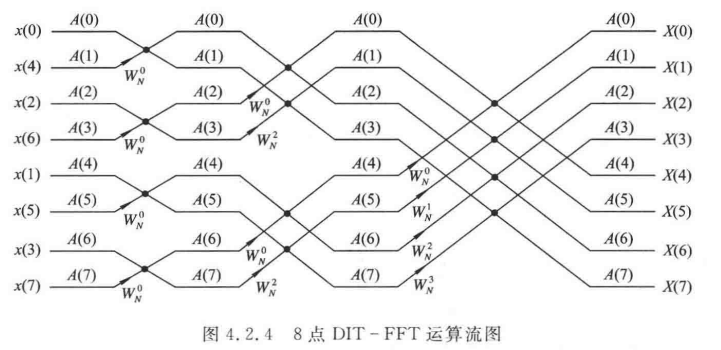
2. 画 8 点基 2-DIT（时域抽取）-FFT 和基 2-DIF（频域抽取）-FFT 流图

公共运算：

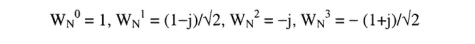
1. 8点DIT-FFT

2. 8点DIF-FFT

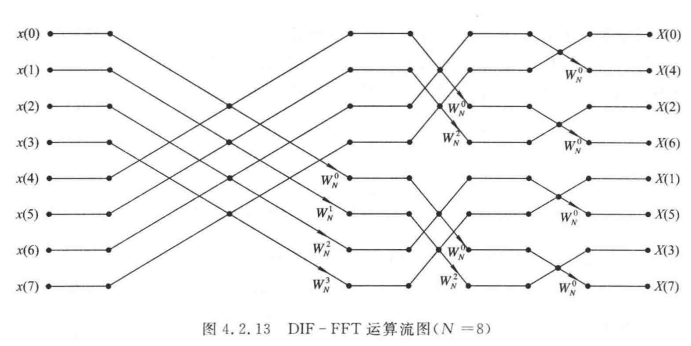
3. 会手算有限长序列的 DFT

就是带公式

---

五、z 逆变换

1. 求z逆变换

如

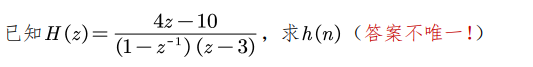
2. 根据 H(z) 表达式写出零极点、收敛域

3. 会判断在何收敛域情况下， 是因果的/非因果的，以及稳定的/不稳定的

---

六、用 DFT 估计频谱（✔️ ）

1. 仅仅通过补零，能否改善频谱估计的物理分辨率？

• 不能

2. 仅仅通过补零，能减少 栅栏 效应，改善频谱估计的 频率 分辨率。

---

七、低通数字滤波器设计

1.设计步骤

2. 注意点

八、序列抽取与插值

1. 如何用数学表达式和框图表示 L 倍抽取？

实际应用中，为了避免频域混叠，在抽取前需要添加低通滤波器。

---

九、随机信号的基本概念

1. 平稳性与各态历经性

2. 方差、互协方差、均方值、自相关函数和功率谱之间的关系是什么？

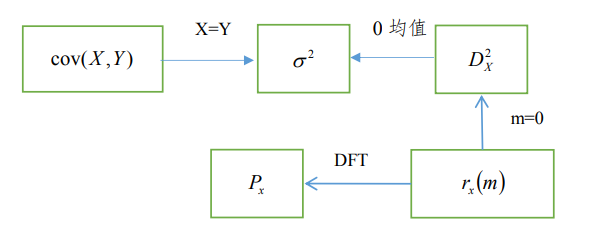
3. 白噪声自相关函数为冲激函数，功率谱为常数。

---

十、自相关函数的直接估计法

重点复习此方法的偏差性能分析：教材 13.1.1 节中第 1 小节“1.偏差”的第508 页部分，公式+结论要点。

---

十一、K-L 变换

1. 零均值宽平稳实随机向量 的协方差矩阵 的非对角元绝对值越大，说明各元素之间的相关性越_强_？（强/弱）

2. K-L 变换 y=Ax 的目的是什么？教材 P327 关于 K-L 变换优点的讨论 ①。

K-L变换是Karhunen-Loeve变换的简称，这是一种特殊的正交变换，主要用于一维和二维信号的数据压缩。

• 举例：对给定的信号x(n),若它是正弦信号，那么不管它有多长，我们仅需三个参数，即幅度、频率和相位，便可完全确定它。当我们需要对x(n)进行传输或存储时，仅需传输或存储这三个参数。在接收端，由于这三个参数可完全无误差地恢复出原信号，因此达到了数据最大限度的压缩。对大量的非正弦信号，如果它的各个分量之间完全不相关，那么表示该数据中没有沉余，需要全部传输或存储；若x(n)中有相关成分，通过去除其相关性则可达到数据压缩的目的。

优点：

3. K-L 变换后 y 的协方差阵C_y 与 C_x 的关系？教材 P326 公式(8.2.2)前半部分

4. 其他

---

十二、ARMA、AR、MA 模型以及参数谱估计