树链剖分（维护树上信息）

news2024/9/29 17:58:02

学习前请先掌握线段树：线段树（维护区间信息）

一，思想：

将一颗树拆成多条线性链以方便维护（如线段树）。

先给出以下定义（通过这些定义我们就可以组成链）：

  1. 重儿子：子节点最多的儿子就是重儿子
  2. 轻儿子：除了重儿子，其余都是轻儿子
  3. 重边：连接重儿子的边。
  4. 轻边：除了重边，其余都是轻边
  5. 重链：这条链上的边都是重边

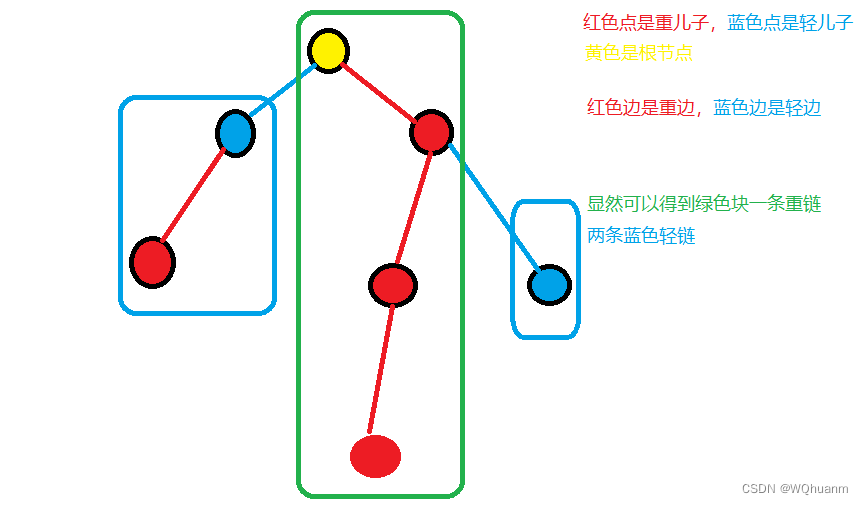
 1，建树：

在dfs1中我们需要遍历这颗树，建立每个点的父子关系，并统计每个点的子节点数，从而得出其重儿子

void dfs1(int u, int f)
{
	fa[u] = f;//存储u点父亲
	dep[u] = dep[f] + 1;//深度是父亲深度+1
	tot[u] = 1, son[u] = idx[u] = 0;//tot是子节点（包括自己）的数量，son是重儿子，idx是u的重新编号，对这3个初始化
	int maxn = -1;
	for (int i = head[u]; i; i = edge[i].next)
		{
			int v = edge[i].to;
			if (v == f)continue;
			dfs1(v, u);
			tot[u] += tot[v];//增加u的子节点数
			if (tot[v] > maxn)maxn = tot[v], son[u] = v;//更新重儿子
		}
}

2，重新编号形成线性链

  1. 我们要对一条线性链操作，显然要求链上的点连续。因此我们需要给点重新编号。即从跟节点开始，每次优先给重儿子编号，这样这颗树最后就形成（同一条链是的点编号连续（因为优先给重儿子编号且优先以重儿子建链）并且子树内的点也是连续的）。
  2. 当然，我们需要知道链的端点，所以我们每个点都存储他所在链的顶点top。

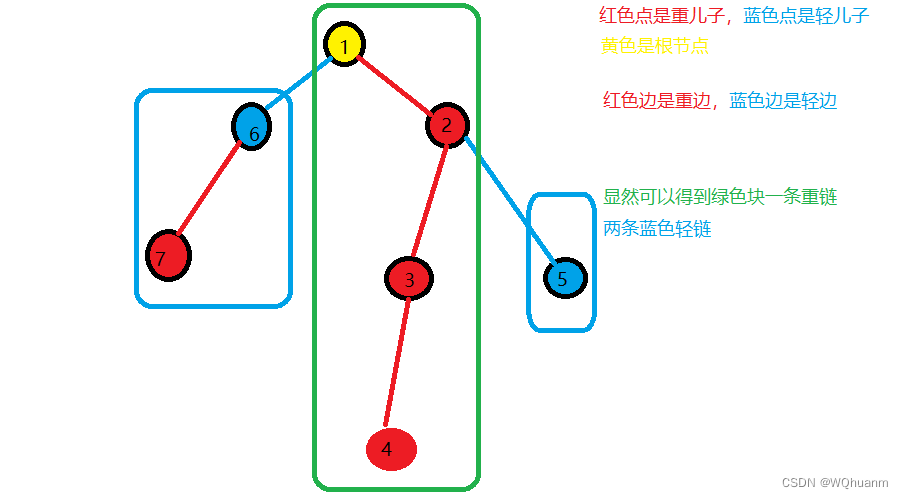
 我们dfs2实现的功能就是新编号，并记录每个点的top。观察上图我们发现，轻儿子就是一条新链的开端，所以他开新链时自己就是top

void dfs2(int u, int topfa)
{
	top[u] = topfa;//记录链顶点
	idx[u] = ++cnt;//新编号，从根节点的1不断编号
	a[cnt] = b[u];//把原来编号的值存入新编号的值
	if (!son[u])return;//如果没用儿子就不用往下
	dfs2(son[u], topfa);//有儿子先访问重儿子（重儿子优先编号）
	for (int i = head[u]; i; i = edge[i].next)
		{
			int v = edge[i].to;
			if (!idx[v])dfs2(v, v);//idx为0，说明没用编号（也说明一定不是重儿子），进行编号，v自己是轻链顶点
		}
}

3，树上更新操作

更新x到y：

  1. 如果x，y是同一条链，那他们在连续区间内，直接更新。
  2. 如果不是，我们显然是更新完当前链（优先更新深度大的链，这样才能不断将两条链往上跳），然后跳到链上方的链进行更新（与lca一个原理），直到新x，y是同一条链，进行操作1。

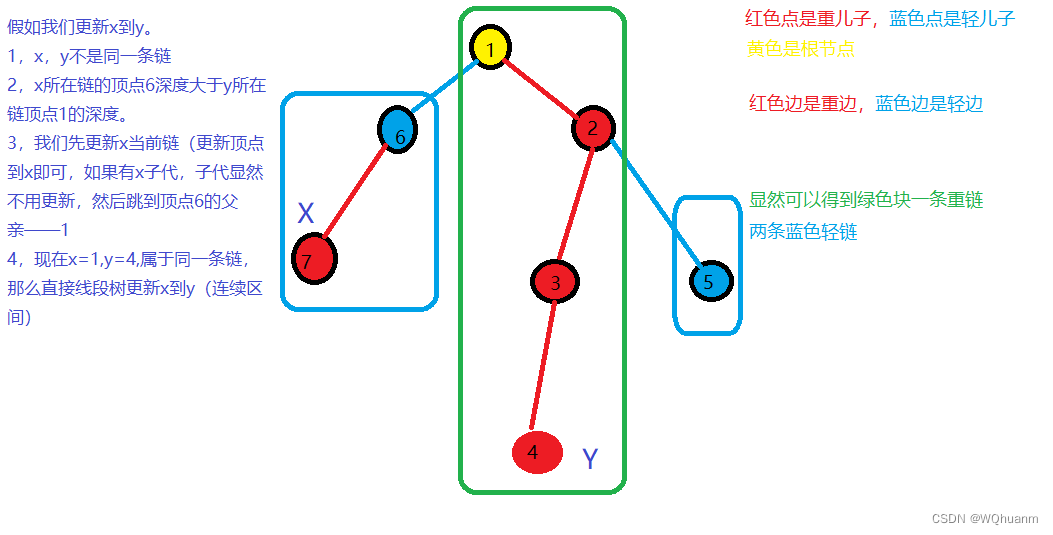
void treeadd(int x, int y, ll z)
{
	while (top[x] != top[y])//不是同一条链，就更新到是为止
		{
			if (dep[top[x]] < dep[top[y]])swap(x, y);//为了方便，始终保持x所在链的顶点深度大（注意，比较的是顶点深度，不是x与y深度
			update(idx[top[x]], idx[x], 1, z);//链是连续区间，直接线段树更新
			x = fa[top[x]];//x成为顶点父亲
		}
	if (dep[x] > dep[y])swap(x, y);//出来后，为了方便，让x深度小，因为我们的线段树必须更新小编号到大编号
	update(idx[x], idx[y], 1, z);
}

4，树上查询

跟更新没什么区别

ll treeask(int x, int y)
{
	ll ans = 0;
	while (top[x] != top[y])//不是同一条链，就不断累加经过的链的区间的值
		{
			if (dep[top[x]] < dep[top[y]])swap(x, y);
			ans = (ans + ask(idx[top[x]], idx[x], 1)) % mod;
			x = fa[top[x]];
		}
	if (dep[x] > dep[y])swap(x, y);
	ans = (ans + ask(idx[x], idx[y], 1)) % mod;
	return ans % mod;
}

5，求lca，因为我们树链建好，也可以用于求lca，很显然两个点同步到同一条链（都是不断往祖先跳），此时谁深度小谁就是他们的LCA

ll lca(int u, int v)
{
	while (top[u] != top[v])
		{
			if (dep[top[u]] > dep[top[v]])u = fa[top[u]];//所在链顶点深度大的求往祖先跳
			else v = fa[top[v]];
		}
	return dep[u] > dep[v] ? v : u;
}

二，模板题：P3384 【模板】重链剖分/树链剖分

思路：

操作1，2上面都说过了。

操作3，4也很显然：我们说过，同一个子树是连续区间的点，如果父节点是x(线段树上编号idx[x]），那么树的最后一个点就是idx[x]+tot[x]-1。（tot[x]记录x子树上的节点数（包括x））。

#include <bits/stdc++.h>
using namespace std;
#define ll     long long
#define int ll
const int N = 1e5 + 10;

int n, m, r, mod, num, cnt;
int head[N << 1], tot[N], dep[N], fa[N], son[N], top[N], idx[N];
int a[N], b[N];
struct node
{
	int next, to;
} edge[N << 1];
struct tree
{
	int l, r;
	int sum, add;
} t[4 * N + 2];

void add(int u, int v)
{
	edge[++num].next = head[u];
	edge[num].to = v;
	head[u] = num;
}

void dfs1(int u, int f)
{
	fa[u] = f;//存储u点父亲
	dep[u] = dep[f] + 1;//深度是父亲深度+1
	tot[u] = 1, son[u] = idx[u] = 0;//tot是子节点（包括自己）的数量，son是重儿子，idx是u的重新编号，对这3个初始化
	int maxn = -1;
	for (int i = head[u]; i; i = edge[i].next)
		{
			int v = edge[i].to;
			if (v == f)continue;
			dfs1(v, u);
			tot[u] += tot[v];//增加u的子节点数
			if (tot[v] > maxn)maxn = tot[v], son[u] = v;//更新重儿子
		}
}

void dfs2(int u, int topfa)
{
	top[u] = topfa;//记录链顶点
	idx[u] = ++cnt;//新编号，从根节点的1不断编号
	a[cnt] = b[u];//把原来编号的值存入新编号的值
	if (!son[u])return;//如果没用儿子就不用往下
	dfs2(son[u], topfa);//有儿子先访问重儿子（重儿子优先编号）
	for (int i = head[u]; i; i = edge[i].next)
		{
			int v = edge[i].to;
			if (!idx[v])dfs2(v, v);//idx为0，说明没用编号（也说明一定不是重儿子），进行编号，v自己是轻链顶点
		}
}

//---------以下是线段树代码-------//
void build(int l, int r, int p)
{
	t[p].l = l, t[p].r = r;
	if (l == r)
		{
			t[p].sum = a[l] % mod;
			return;
		}
	int mid = l + ((r - l) >> 1);
	build(l, mid, p << 1);
	build(mid + 1, r, p << 1 | 1);
	t[p].sum = (t[p << 1].sum + t[p << 1 | 1].sum) % mod;
}

void lazy(int p)
{
	if (t[p].l == t[p].r)t[p].add = 0;
	if (t[p].add)
		{
			t[p << 1].sum = (t[p << 1].sum + t[p].add * (t[p << 1].r - t[p << 1].l + 1)) % mod;
			t[p << 1 | 1].sum = (t[p << 1 | 1].sum + t[p].add * (t[p << 1 | 1].r - t[p << 1 | 1].l + 1)) % mod;
			t[p << 1].add = (t[p << 1].add + t[p].add) % mod;
			t[p << 1 | 1].add = (t[p << 1 | 1].add + t[p].add) % mod;
			t[p].add = 0;
		}
}

void update(int l, int r, int p, ll z)
{
	if (l <= t[p].l && t[p].r <= r)
		{
			t[p].sum = (t[p].sum + z * (t[p].r - t[p].l + 1)) % mod;
			t[p].add = (t[p].add + z) % mod;
			return;
		}
	lazy(p);
	int mid = t[p].l + ((t[p].r - t[p].l) >> 1);
	if (l <= mid)update(l, r, p << 1, z);
	if (r > mid)update(l, r, p << 1 | 1, z);
	t[p].sum = (t[p << 1].sum + t[p << 1 | 1].sum) % mod;
}

ll ask(int l, int r, int p)
{
	if (l <= t[p].l && t[p].r <= r)return t[p].sum % mod;
	lazy(p);
	int mid = t[p].l + ((t[p].r - t[p].l) >> 1);
	ll ans = 0;
	if (l <= mid)ans = (ans + ask(l, r, p << 1)) % mod;
	if (r > mid)ans = (ans + ask(l, r, p << 1 | 1)) % mod;
	return ans;
}
//------以上是线段树代码------//

void treeadd(int x, int y, ll z)
{
	while (top[x] != top[y])//不是同一条链，就更新到是为止
		{
			if (dep[top[x]] < dep[top[y]])swap(x, y);//为了方便，始终保持x所在链的顶点深度大（注意，比较的是顶点深度，不是x与y深度
			update(idx[top[x]], idx[x], 1, z);//链是连续区间，直接线段树更新
			x = fa[top[x]];//x成为顶点父亲
		}
	if (dep[x] > dep[y])swap(x, y);//出来后，为了方便，让x深度小，因为我们的线段树必须更新小编号到大编号
	update(idx[x], idx[y], 1, z);
}

ll treeask(int x, int y)
{
	ll ans = 0;
	while (top[x] != top[y])//不是同一条链，就不断累加经过的链的区间的值
		{
			if (dep[top[x]] < dep[top[y]])swap(x, y);
			ans = (ans + ask(idx[top[x]], idx[x], 1)) % mod;
			x = fa[top[x]];
		}
	if (dep[x] > dep[y])swap(x, y);
	ans = (ans + ask(idx[x], idx[y], 1)) % mod;
	return ans % mod;
}
//这模板题用不到
ll lca(int u, int v)
{
	while (top[u] != top[v])
		{
			if (dep[top[u]] > dep[top[v]])u = fa[top[u]];//所在链顶点深度大的求往祖先跳
			else v = fa[top[v]];
		}
	return dep[u] > dep[v] ? v : u;
}

int32_t main()
{
	cin >> n >> m >> r >> mod;
	for (int i = 1; i <= n; ++i)cin >> b[i];
	int h, x, y, z;
	for (int i = 1; i < n; ++i)
		{
			cin >> x >> y;
			add(x, y), add(y, x);
		}
	dfs1(r, 0);
	dfs2(r, r);
	build(1, n, 1);
	while (m--)
		{
			cin >> h;
			if (h == 1)
				{
					cin >> x >> y >> z;
					treeadd(x, y, z);
				}
			else if (h == 2)
				{
					cin >> x >> y;
					cout << treeask(x, y) << endl;
				}
			else if (h == 3)
				{
					cin >> x >> z;
					update(idx[x], idx[x] + tot[x] - 1, 1, z);
				}
			else if (h == 4)
				{
					cin >> x;
					cout << ask(idx[x], idx[x] + tot[x] - 1, 1) << endl;
				}
		}
	return 0;
}

三：例题：The LCIS on the Tree

思路：

很考验细节...

重点就是对区间合并时的操作与区间的维护

我们对于一段区间需要维护

fl:左降序，sl:左升序，fr:右降序，sr：右升序

左右端点值：lnum，rnum

区间边界：l，r

区间降序最大长度：fmaxn，区间升序最大长度：smaxn

区间节点数：size（用于决定该区间是否为空）

#include <bits/stdc++.h>
using namespace std;
#define ll     long long
const int N = 1e5 + 10;

int a[N], b[N], top[N], tot[N], dep[N], head[N], son[N], fa[N], idx[N];
int num, cnt, n, m;

struct node
{
	int next, to;
} edge[N];

struct tree
{
	int l, r, lnum, rnum, size;
	int fl, fr, sl, sr;
	int fmaxn, smaxn;
	void init()
	{
		lnum = rnum = fl = fr = sl = sr = size = fmaxn = smaxn = 0;
	}
	void reverse()//用于把这个tree区间左右信息互换
	{
		swap(fl, sr), swap(sl, fr), swap(lnum, rnum);
		swap(fmaxn, smaxn);
	}
} t[4 * N];

void add(int u, int v)
{
	edge[++num].next = head[u];
	edge[num].to = v;
	head[u] = num;
}
void init()
{
	memset(head, 0, sizeof(head));
	num = cnt = 0;
}

void dfs1(int u, int f)
{
	fa[u] = f;
	dep[u] = dep[f] + 1;
	tot[u] = 1, son[u] = idx[u] = 0;
	int maxn = -1;
	for (int i = head[u]; i; i = edge[i].next)
		{
			int v = edge[i].to;
			if (v == f)continue;
			dfs1(v, u);
			tot[u] += tot[v];
			if (tot[v] > maxn)maxn = tot[v], son[u] = v;
		}
}

void dfs2(int u, int topfa)
{
	top[u] = topfa;
	idx[u] = ++cnt;
	a[cnt] = b[u];
	if (!son[u])return;
	dfs2(son[u], topfa);
	for (int i = head[u]; i; i = edge[i].next)
		{
			int v = edge[i].to;
			if (!idx[v])dfs2(v, v);
		}
}

tree unit(tree l, tree r)
{
	if (!l.size)return r;//如果左树没用节点（为空），那直接放回右部分即可
	if (!r.size)return l;//同理
	tree t;
	t.l = l.l, t.r = r.r;
	t.size = l.size + r.size;//sized等于左边加右边
	t.lnum = l.lnum, t.rnum = r.rnum;
	t.fl = l.fl;
	if (l.fl == l.size && l.rnum > r.lnum)t.fl += r.fl;
	t.sl = l.sl;
	if (l.sl == l.size && l.rnum < r.lnum)t.sl += r.sl;
	t.fr = r.fr;
	if (r.fr == r.size && l.rnum > r.lnum)t.fr += l.fr;
	t.sr = r.sr;
	if (r.sr == r.size && l.rnum < r.lnum)t.sr += l.sr;
//以降序fmaxn为例，更新时要么去左边的fmaxn，要么右边的fmaxn，要么如果两边符合端点l.rnum > r.lnum，则可以多算中间一段
	t.fmaxn = max(l.fmaxn, max(r.fmaxn, (l.rnum > r.lnum ? l.fr + r.fl : 0)));
	t.smaxn = max(l.smaxn, max(r.smaxn, (l.rnum < r.lnum ? l.sr + r.sl : 0)));

	return t;
}

void change(int p)
{
	t[p] = unit(t[p << 1], t[p << 1 | 1]);
}

void build(int l, int r, int p)
{
	t[p].l = l, t[p].r = r;
	if (l == r)
		{
			t[p].lnum = t[p].rnum = a[l];
			t[p].size = t[p].fmaxn = t[p].smaxn = t[p].fl = t[p].sl = t[p].sr = t[p].fr = 1;
			return ;
		}
	int mid = l + ((r - l) >> 1);
	build(l, mid, p << 1);
	build(mid + 1, r, p << 1 | 1);
	change(p);
}

tree ask(int l, int r, int p)
{
	if (l <= t[p].l && t[p].r <= r)return t[p];
	int mid = t[p].l + ((t[p].r - t[p].l) >> 1);
	//如果l，r范围只在左右区间一边，直接返回那一边得到的tree即可
	if (r <= mid)return ask(l, r, p << 1);
	if (l > mid)return ask(l, r, p << 1 | 1);
	tree t, tl, tr;
	tl = ask(l, r, p << 1), tr = ask(l, r, p << 1 | 1);
	return (t = unit(tl, tr));
}

int treeask(int x, int y)
{
	bool flag = 0;
	tree l, r;
	//我们刚刚开始tree是空的，记得初始化，否则与别人连接出问题
	l.init();
	r.init();
	while (top[x] != top[y])
		{
			if (dep[top[x]] < dep[top[y]])swap(x, y), swap(l, r), flag ^= 1;//x,y每次翻转记录一下
			tree tmp = ask(idx[top[x]], idx[x], 1);
			l = unit(tmp, l);//越往上的段在左边
			x = fa[top[x]];
		}
	if (dep[x] > dep[y])swap(x, y), swap(l, r), flag ^= 1;
	tree tmp = ask(idx[x], idx[y], 1);//x深度小于y，则这一段跟y的链拼接
	r = unit(tmp, r);
	if (flag)swap(l, r);//如果翻转奇数次，那么我们最后得出结果是y->x，所以我们需要否则回来
	l.reverse();//最后是x的顶端拼接y的端点，显然需要将x左右翻转
	return unit(l, r).smaxn;
}

int main()
{
	std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	int t, x, y;
	cin >> t;
	for (int ti = 1; ti <= t; ++ti)
		{
			init();
			cin >> n;
			for (int i = 1; i <= n; ++i)cin >> b[i];
			for (int i = 2; i <= n; ++i)
				{
					cin >> x;
					add(x, i);
				}
			dfs1(1, 0);
			dfs2(1, 1);
			build(1, n, 1);
			cin >> m;
			cout << "Case #" << ti << ":" << endl;
			while (m--)
				{
					cin >> x >> y;
					cout << treeask(x, y) << endl;
				}
			if (ti < t)cout << endl;
		}

	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/380940.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Docker概念介绍

Docker概念介绍

目录 1、传统方式、虚拟化、容器部署方式的区别 2、为什么会有docker 3、什么是docker 4、docker的优势 5、Docker组成部分 6、docker镜像的原理介绍 7、 容器应用场景 8、Docker资源汇总 了解docker之前&#xff0c;我们要先了解部署方式有哪些&#xff0c;各有什么优缺点…
阅读更多...
Windows 右键菜单扩展容器 [开源]

Windows 右键菜单扩展容器 [开源]

今天给大家分享一个我做的小工具&#xff0c;可以自定义扩展右键菜单的功能来提高工作效率&#xff0c;效果图如下&#xff1a; 如上图&#xff0c;右键菜单多了几个我自定义的菜单&#xff1a; 复制文件路径 复制文件夹路径 我的工具箱 <走配置文件动态创建子菜单&#x…
阅读更多...
cesium封装实现配置格网及插值高程面实现

cesium封装实现配置格网及插值高程面实现

一、数据结构建模二、插值算法得到的插值结果三、图层配置primitiveGrid:{isRLayerPanel: true,primitives:[],url: /static/data/Grid.json,dataPath: ,dataIdField: code,options:{id:primitiveGrid,name:格网,type:grid,isShow: false},location: {"destination":…
阅读更多...
Hive中的基础函数(一)

Hive中的基础函数(一)

一、hive中的内置函数根据应用归类整体可以分为8大种类型。 1、 String Functions 字符串函数 主要针对字符串数据类型进行操作&#xff0c;比如下面这些&#xff1a; 字符串长度函数&#xff1a;length •字符串反转函数&#xff1a;reverse •字符串连接函数&#xff1a;…
阅读更多...
Word处理控件Aspose.Words功能演示：使用 C++ 在 Word 文档 (DOC/DOCX) 中插入表格

Word处理控件Aspose.Words功能演示：使用 C++ 在 Word 文档 (DOC/DOCX) 中插入表格

Aspose.Words 是一种高级Word文档处理API&#xff0c;用于执行各种文档管理和操作任务。API支持生成&#xff0c;修改&#xff0c;转换&#xff0c;呈现和打印文档&#xff0c;而无需在跨平台应用程序中直接使用Microsoft Word。此外&#xff0c; Aspose API支持流行文件格式处…
阅读更多...
基于python的多线程数据库数据录入

基于python的多线程数据库数据录入

说明&#xff1a; 使用python编程结合多线程技术&#xff0c;将已经在python文件中的数据批量写入到数据库&#xff0c;便于数据关系结构化管理。 环境配置&#xff1a; certifi2019.6.16 chardet3.0.4 idna2.8 PyMySQL0.9.3 requests2.22.0 urllib31.25.3 将所需要的环境保…
阅读更多...
vue模板语法和数据绑定和el、data的两种

vue模板语法和数据绑定和el、data的两种

vue模板语法有两大类&#xff1a; 1.插值语法&#xff1a; 功能&#xff1a;用于解拆标签体内容 写法&#xff1a;{{xxx}}&#xff0c;xxx是js表达式&#xff0c;且可以直接读取到data中的所有属性 2.指令语法&#xff1a; 功能&#xff1a;用于解拆标签&#xff08;包括&…
阅读更多...
《商用密码应用与安全性评估》第一章密码基础知识1.1应用概念

《商用密码应用与安全性评估》第一章密码基础知识1.1应用概念

密码的概念与作用 概念 密码&#xff1a;采用特定变换的方法对信息进行加密保护、安全认证的技术、产品和服务。 密码技术&#xff1a;密码编码、实现、协议、安全防护、分析破译、以及密钥产生、分发、传递、使 用、销毁等技术。 密码技术核心&#xff1a;密码算法…
阅读更多...
家用洗地机什么品牌质量好耐用?最适合家用的洗地机

家用洗地机什么品牌质量好耐用?最适合家用的洗地机

近些年&#xff0c;随着消费水平的不断升级&#xff0c;我们对家电产品的要求也在逐步提高&#xff0c;就以这几年非常流行的洗地机为例&#xff0c;如今的人们在选洗地机时&#xff0c;会综合考虑价位、技术、配置、颜值、功能等多个方面&#xff0c;那么市场上家用洗地机什么…
阅读更多...
JAVACC

JAVACC

JavaCC全称为Java Compiler Compiler&#xff0c;它是一个生成器&#xff0c;用于生成词法分析器&#xff08;lexical analysers&#xff09;和语法分析器&#xff08;parsers&#xff09;&#xff1b;JavaCC本身并不是词法分析器和语法分析器&#xff0c;它是一个生成器&#…
阅读更多...
mysql数据库之索引结构

mysql数据库之索引结构

MySQL的索引是在存储引擎层实现的&#xff0c;不同的存储引擎有不同的结构。 一、常见索引。 索引结构描述BTree索引最常见的索引类型&#xff0c;大部分引擎都支持B树索引Hash索引底层数据结构是用哈希表实现的&#xff0c;只有精确匹配索引列的查询才有效&#xff0c;不支持…
阅读更多...
Web版和客户端哪种SQL工具更好？ChatGPT有话要说

Web版和客户端哪种SQL工具更好？ChatGPT有话要说

2023年年初公司发布了一款Web版SQL工具&#xff0c;短期内就赢得了众多用户的喜爱和下载。不过&#xff0c;也有SQL用户在评论区中提出自己的观点&#xff0c;认为Web版工具都不可靠&#xff0c;甚至看见Web版工具就劝返… … 工具Web化逐渐成为一种趋势&#xff0c;比如&…
阅读更多...
如何使用Bypass-Url-Parser实现URL绕过并访问40X受保护页面

如何使用Bypass-Url-Parser实现URL绕过并访问40X受保护页面

关于Bypass-Url-Parser Bypass-Url-Parser是一款功能强大的URL绕过工具&#xff0c;该工具可以使用多种方法实现URL绕过并访问目标站点的40X受保护页面。 工具下载 由于该工具基于Python 3 开发&#xff0c;因此我们首先需要在本地设备上安装并配置好Python 3环境。接下来&a…
阅读更多...
PLC实验—西门子S7 1200读取超声波传感器数据

PLC实验—西门子S7 1200读取超声波传感器数据

PLC实验—西门子S7 1200读取超声波传感器数据 US-016超声波测距模块 实验箱上是US-016超声波测距模块&#xff0c;其有关信息可以看实验室的博客 US-016超声波测距模块 1号Pin&#xff1a;接VCC电源&#xff08;直流5V&#xff09; 2号Pin&#xff1a;量程设置引脚&#xff…
阅读更多...
GWT安装过程

GWT安装过程

1:安装前准备 &#xff08;可以问我要&#xff09; appengine-java-sdk-1.9.8 com.google.gdt.eclipse.suite.4.3.update.site_3.8.0 gwt-2.5.1 eclipse-jee-kepler-SR2-win32-x86_64.zip 2&#xff1a;安装环境上 打开eclipse Help –Install New Software… 选择Add –…
阅读更多...
如何使用工时表管理项目和非项目的资源？

如何使用工时表管理项目和非项目的资源？

对新机会做出反应的能力是企业竞争优势的关键。项目不断涌现&#xff0c;企业需要了解具体的可用性以及是否有资源来接受新事物。更进一步来说&#xff0c;企业需要知道员工将时间花在哪里。 使用 8Manage工时表解决方案&#xff0c;你将始终拥有做出正确业务决策所需的全面知…
阅读更多...
vue源码分析-响应式系统工作原理

vue源码分析-响应式系统工作原理

上一章&#xff0c;我们讲到了Vue初始化做的一些操作&#xff0c;那么我们这一章来讲一个Vue核心概念响应式系统。 我们先来看一下官方对深入响应式系统的解释: 当你把一个普通的 JavaScript 对象传给 Vue 实例的 data 选项&#xff0c;Vue 将遍历此对象所有的属性。 并使用 O…
阅读更多...
LeetCode:构造最大二叉树；使用中序和后序数组构造二叉树；使用前序和中序数组遍历二叉树。

LeetCode:构造最大二叉树；使用中序和后序数组构造二叉树；使用前序和中序数组遍历二叉树。

构造二叉树最好都是使用前序遍历&#xff1b;中左右的顺序。 654. 最大二叉树 中等 636 给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建: 创建一个根节点&#xff0c;其值为 nums 中的最大值。递归地在最大值 左边 的 子数组前缀上 构建…
阅读更多...
人力资源管理系统

人力资源管理系统

技术&#xff1a;Java、JSP等摘要&#xff1a;在当今的信息化社会&#xff0c;为了更有效率地工作&#xff0c;人们充分利用现在的电子信息技术&#xff0c;在办公室架设起办公服务平台&#xff0c;将人力资源相关信息统一起来管理&#xff0c;帮助管理者有效组织降低成本和加速…
阅读更多...
【Linux】gcc/g++/gdb的使用

【Linux】gcc/g++/gdb的使用

&#x1f525;&#x1f525; 欢迎来到小林的博客&#xff01;&#xff01;       &#x1f6f0;️博客主页&#xff1a;✈️小林爱敲代码       &#x1f6f0;️社区 : 进步学堂       &#x1f6f0;️欢迎关注&#xff1a;&#x1f44d;点赞&#x1f64c;收…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023