1.模型描述

有训练集数据房子面积和卖出的价钱，我们用这组数据来模拟特定面积的房子能够卖出的价钱。

这是一个很明显的监督学习（supervised learning）的例子，因为我们的训练集里包含了正确的结果（即房子的卖价）。同时这也是典型的回归问题（regression），因为模型的输出是一个连续的数值。

下面定义模型中会用到的一些符号：

m：表示训练集中的数据个数

x：训练集中输入变量

y：训练集中输出变量

（x，y）：训练集中的一个数据

：第i个训练集数据

如上图x（1）=2104，y（2）=232

现在来看监督学习如何做这件事，我们首先向计算机提供训练集，计算机根据学习算法从训练集中学习数据特征并输出一个假设函数h（hypothesis function），h是一个x到y的映射函数。输入房子面积x来预测卖价y。

在这里，我们首先考虑最简单的情况，即房子的卖价与面积为一元线性函数关系：

我们现在要做的就是要找到合适的θ0和θ1来使得训练集中的数据到假设函数的距离最小，达到最好的拟合效果，那么如何找呢？

2.代价函数

我们需要一个具体的函数表达式来表示我们的假设函数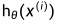到训练集中输出数据y的距离，定义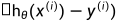为距离，为了后续方便，我们将式子平方并对所有的训练数据进行求和(i从1到m）,最后对式子进行平均得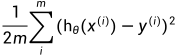。这就是我们的代价函数，记作。

将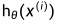写开得：

我们的目标就是要求出满足假设函数h到y最小距离的，，即minimize，从而确定，的值。

需要特别注意的是，在假设函数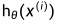中的自变量为x。在代价函数中自变量为，。

当我们有两个参数，时，我们绘制出来的代价函数可能是这样的：

从图中可以看出，对于同样高度的，和可以取不同的值，但是存在唯一的，使得取得最小值，而满足该条件的，即为所求。

为了得出满足该条件的，，我们使用线性回归中的梯度下降算法来一步步求得minimize，从而得出满足该条件的，。

3.梯度下降算法

我们用梯度下降算法来最小化线性回归中的代价函数。

算法的实施步骤：

1. 我们首先将，赋初值，一般我们将两者都设为0

2. 然后我们不断地改变，的值去减少，直到我们得到最小值为止

3.1梯度下降算法背后的数学原理

3.1.1 梗概

（for j=0 and j=1)：在对，进行赋值后，我们通过该式进行，的更新(:=表示将等号右边的值赋给等号左边)。

α为学习率（learning rate），也叫步长，可以形象的理解为上图下山过程中下山的步长，控制我们以多大的幅度来更新，，而为代价函数对与的偏导。

正确的求偏导方法为：同步更新，即根据给定的(，）来同步更新，；而不是先更新，再用更新好的来更新。具体更新步骤如下：

正确更新：

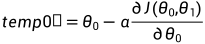
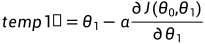
错误更新：

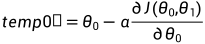
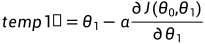
（，更新不同步）

3.1.2 重点介绍偏导部分

我们首先假设只有一个参数的情形，如下图：

：学习率α始终是正的，当在局部最低点右侧时，（即曲线在处的斜率）为正，此时减去的是一个正值，即向着横坐标的负方向（即局部最低点所在方向移动），此时更新的一定比原始的的值要小，从而使代价函数逐步变小。

同样的道理看下图：

：学习率α始终是正的，当在局部最低点左侧时，（即曲线在处的斜率）为负，此时减去的是一个负值，即向着横坐标的正方向（即局部最低点所在方向移动），此时更新的一定比原始的的值要小，从而使代价函数逐步变小。

3.1.4 学习率

下面我们来研究学习率对梯度下降的影响。我们来看两种极端情况：

1. 学习率太小

。由式子可知，当α很小时，新更新的的增量将会很小，也即靠近局部最低点（即的最小点，局部最优点）的速度很慢。如图所示：

需要好几步才能到达局部最优点，效率低下。

2. 学习率太大

。由式子可知，当α很大时，新更新的的增量将会很大，因此有可能错过局部最优点，甚至会造成无法收敛乃至发散。如图所示：

3. 思考：如果已处于局部最优点会怎么样？

如果已处于局部最优点，根据最优点的性质可知该点导数为零，则=0，故由公式知新更新的与原来的相同，因此将一直处于局部最优点，，的值不变。

这也解释了即使学习率不变，梯度下降法也可以收敛到局部最低点的原因。因为：

根据梯度下降算法，比如初始在粉红点处，根据此处斜率较大且为正值，故会减少一个较大的量从而到达绿色点处，学习率始终保持不变。同理在绿色点处斜率减小则减小了一个较小的量从而使向左方向移动的步伐放缓而到达红色点处，学习率始终保持不变。再接着此处斜率更小，减小的量更小，到达蓝色点处而学习率不变。以此类推重复上述步骤，我们在接近局部最优点时导数会自动变得越来越小，梯度下降的幅度将会自动变小，则在学习率不变的情况下逐步逼近局部最优点。故即使学习率不变，梯度下降法也可以收敛到局部最优点。

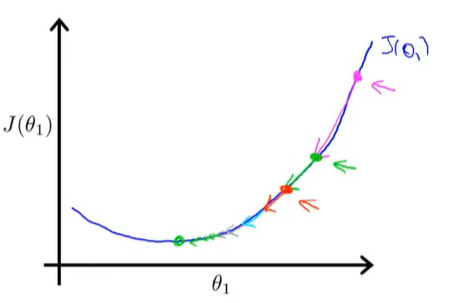
因此我们在梯度下降算法中不必改变学习率。

3.2 梯度下降所存在的问题

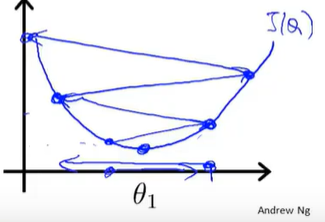
梯度下降存在一个问题，那就是容易陷入到局部最优。

如上图所示，从不同的位置出发（，取不同的初始值），可能会得到不同的局部最优解。这是因为在图中的代价函数存在多个局部最优解。如何解决陷入局部最优的问题会在之后解决。但是在线性回归的代价函数中不存在局部最优，只有一个全局最优，因为线性回归的代价函数图像是这样的：

在这样的代价函数上使用梯度下降，它总会收敛到全局最优，因为没有其他局部最优解。

这种每步梯度下降算法遍历所有训练集样本()来进行参数更新的梯度下降算法叫做Batch梯度下降，因此在计算偏导数时我们计算m个样本的总和

4.线性回归算法

在了解了代价函数和梯度下降算法后，我们就可以引出线性回归算法了。首先对前面的公式进行说明：

假设函数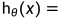：+。假设函数是我们最后要得出的结果，根据假设函数可以预测一个面积的房子可以卖多少钱，而想要得出假设函数就要得出，。

代价函数：。代价函数用来对假设函数预测精度进行度量，判断假设函数的预测精度是否达到最优。（代价函数的值越小，假设函数的预测精度越高，拟合数据拟合的越好）

梯度下降：。通过梯度下降来使得代价函数的值不断达到最优（局部最小值），从而找到最优的假设函数参数，。，的具体更新如下：

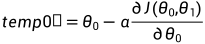
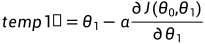
偏导函数：由代价函数，分别对，求偏导可得：==；

==；

:=

:=

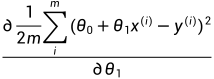算法步骤：

1. 首先我们给，赋初值，一般是=0，=0，得出假设函数。

2. 根据假设函数计算代价函数的值。

3. 计算偏导数带入梯度下降更新，（同时更新）。

4. 根据新得到的，来更新假设函数。

重复2，3，4步，可以发现代价函数的值不断减小，假设函数对于数据的拟合效果越来越好，直至找到最佳的假设函数。