1. 前序遍历

题目链接

解题思路：
非递归遍历一棵树有两点：
1.左路结点 2.左路结点的右子树

什么意思呢？
我们知道前序遍历是按照根，左子树，右子树来的。所以它是先根，然后左子树，根，左子树一直走到左子树为空。

红色的就叫做左路结点。蓝色的就是左路结点的右子树。然后我们再把蓝色的再看作子树划分出左路结点和左路结点的右子树。

大致流程：
在这里我们需要利用一个栈：


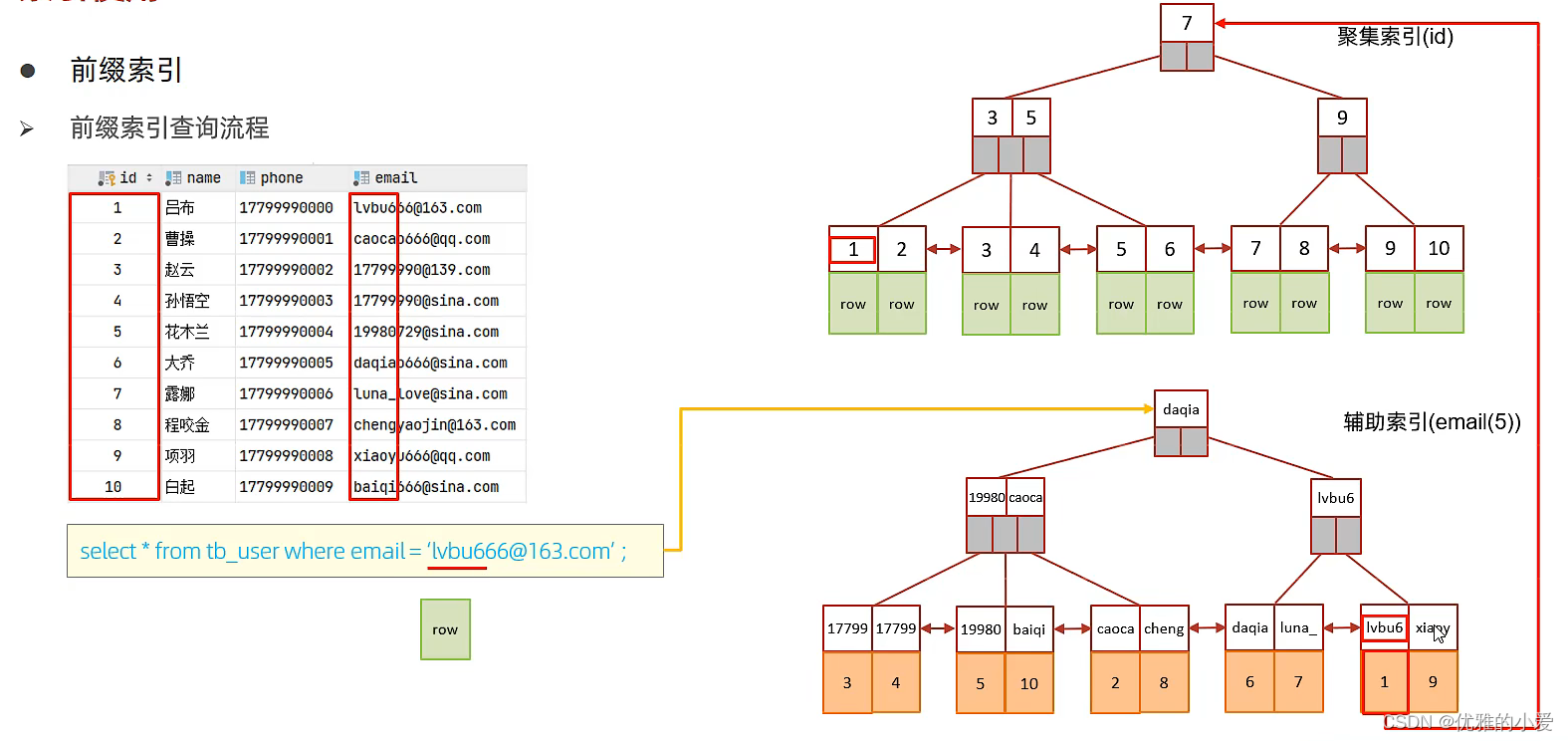
因为走的是前序，根，左子树。所以8，3，1是一开始直接入栈和数组的。

当cur走到1的左子树为空时，我们就要让1出栈，然后走1的右子树。1的右子树也为空。那么我们继续出栈，走的是3的右子树。

然后我们再按照左路结点和左路结点的右子树来划分。走的是6的左子树，6的左子树为空。说明6的左路结点已结束，6出栈，走6的右子树。按照这样的逻辑一直走到10的时候。

10的左子树为空，那么此时10出栈。然后走10的右子树，10的右子树也为空。

当cur和栈都为空时就遍历完了。

代码如下：

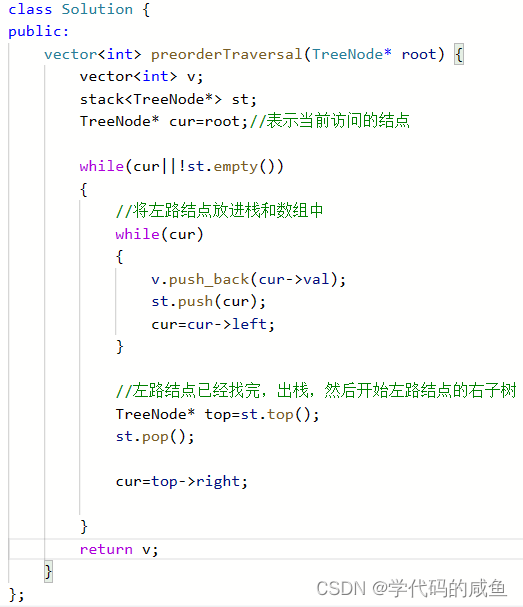
2. 中序遍历

题目链接
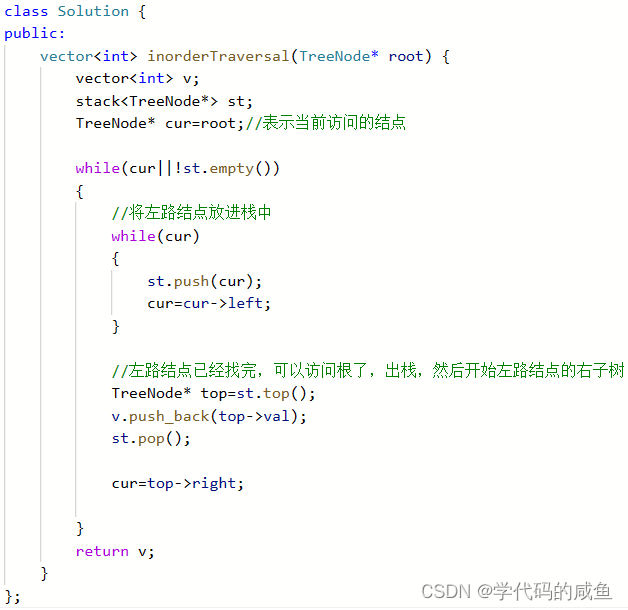
中序遍历和前序遍历的区别不是很大。中序遍历是：左子树，根，右子树。所以，我们中序遍历是左子树访问完了之后，再来访问根。

那么什么时候代表着左子树访问完成了呢？
当我们取出栈顶数据时，代表左子树访问完成了。那么这个时候就可以访问根了！！！

代码如下：

3. 后序遍历

题目链接

后序遍历就不太好弄了。但是还是按照左路结点和左路结点的右子树规则。

按照左路结点先入栈，来到了1的左子树，左子树为空，访问1的右子树。右子树为空，再出栈，访问根。

此时3的左子树访问完了，我们要访问3的右子树。然后按照左路结点和左路结点的右子树继续划分。

6的左子树为空，那么6这颗树的左路结点入栈完成。此时6的右子树不为空，访问6的右子树。7的左子树，右子树都为空。那么就出栈，访问根。此时就可以访问根6了。

那么现在的问题是：第一次遇到6和第二次遇到6，我们怎么区别呢？
如果上一个被访问的结点7是根6的右子树的根，那么说明3的右子树被访问过了，可以访问6了。

所以后序遍历能访问根可以有两个判断：
1.右为空
2.上一个被访问的结点是当前结点的右子树根

代码如下：