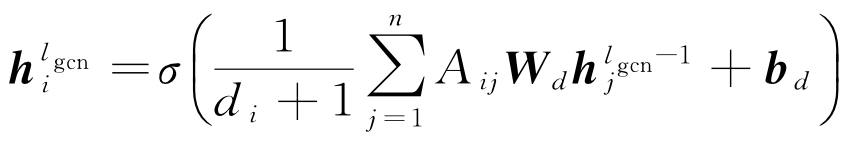概念

• 特征构造的过程中，对特征做分箱处理时必不可少的过程
• 分箱就是将连续变量离散化，合并成较少的状态

分箱的作用

• 离散特征的增加和减少都很容易，易于模型的快速迭代；
• 稀疏向量内积乘法运算速度快，计算结果方便存储，容易扩展；
• 分箱（离散化）后的特征对异常数据有很强的鲁棒性
• 单变量分箱（离散化）为N个后，每个变量有单独的权重，相当于为模型引入了非线性，能够提升模型表达能力
• 分箱（离散化）后可以进行特征交叉，由M+N个变量变为M*N个变量，进一步引入非线性，提升表达能力；
• 分箱（离散化）后，模型会更稳定，如对年龄离散化，20-30为一个区间，不会因为年龄+1就变成一个新的特征。
• 特征离散化以后，可以将缺失作为独立的一类带入模型

等频分箱

红色：目标样本

等距分箱

红色：目标样本

红色：目标样本

*卡方分箱

将卡方值较小的两个相邻箱体合并

使得不同箱体的好坏样本比例区别放大，容易获得高IV

公式

$${\overline{\mathrm{p}}}_{\mathrm{bad}}=\frac{{\sum }_{\mathrm{k}}{\mathrm{n}}_{\mathrm{bad}}^{\mathrm{k}}}{{\sum }_{\mathrm{k}}({\mathrm{n}}_{\mathrm{good}}^{\mathrm{k}}+{\mathrm{n}}_{\mathrm{bad}}^{\mathrm{k}})}$$
$${\chi }_{\mathrm{k}}^2=\frac{({\mathrm{n}}_{\mathrm{bad}}^{\mathrm{k}}-{\overline{\mathrm{p}}}_{\mathrm{bad}}({\mathrm{n}}_{\mathrm{good}}^{\mathrm{k}}+{\mathrm{n}}_{\mathrm{bad}}^{\mathrm{k}}){)}^2}{{\overline{\mathrm{p}}}_{\mathrm{bad}}({\mathrm{n}}_{\mathrm{good}}^{\mathrm{k}}+{\mathrm{n}}_{\mathrm{bad}}^{\mathrm{k}})}$$

k表示第几个箱子

例子

步骤：
初始化：根据连续变量值大小进行排序，构建最初的离散化
合并：遍历相邻两项合并的卡方值，将卡方值最小的两组合并，不断重复直到满足分箱数目要求

	[22-35]	(35-45]	(45-55]	(55-65]	总计
good	3	2	2	1	8
bad	1	2	2	3	8
p					50%
p(good+bad)	2	2	2	2	-
chi2	(1-2)^2/2=1/2	(2-2)^2/2=0	(2-2)^2/2=0	(3-2)^2/2=1/2	-

PBad= 8/16
xk2 = (1-2)^2/2=1/2

卡方值不同代表箱体差异化
使用toad库可以进行卡方分箱代码编写

心得：分箱作为必不可少的一个过程，知道其中原理方可更好的处理数据