我上周在干什么,感觉我上周啥也没训,本来两天一次的vp也没v
很寄啊,再这样下去真不行了
先总结一下如何爆搜:
先去确定好枚举的对象
枚举的对象很重要!!这直接影响了复杂度
然后就是去想递归树就好了
一、确定状态:
状态分为全局变量和局部变量
考虑状态时去考虑三样东西:
阶段(即深度),阶段作为出口
影响决策的因素(全局or局部)
要维护的答案
二、枚举决策+加限定条件
三、确定出口(根据阶段)
那么我们怎么去考虑复杂度:考虑每一层树的结点个数*每个结点的复杂度
92. 递归实现指数型枚举 - AcWing题库
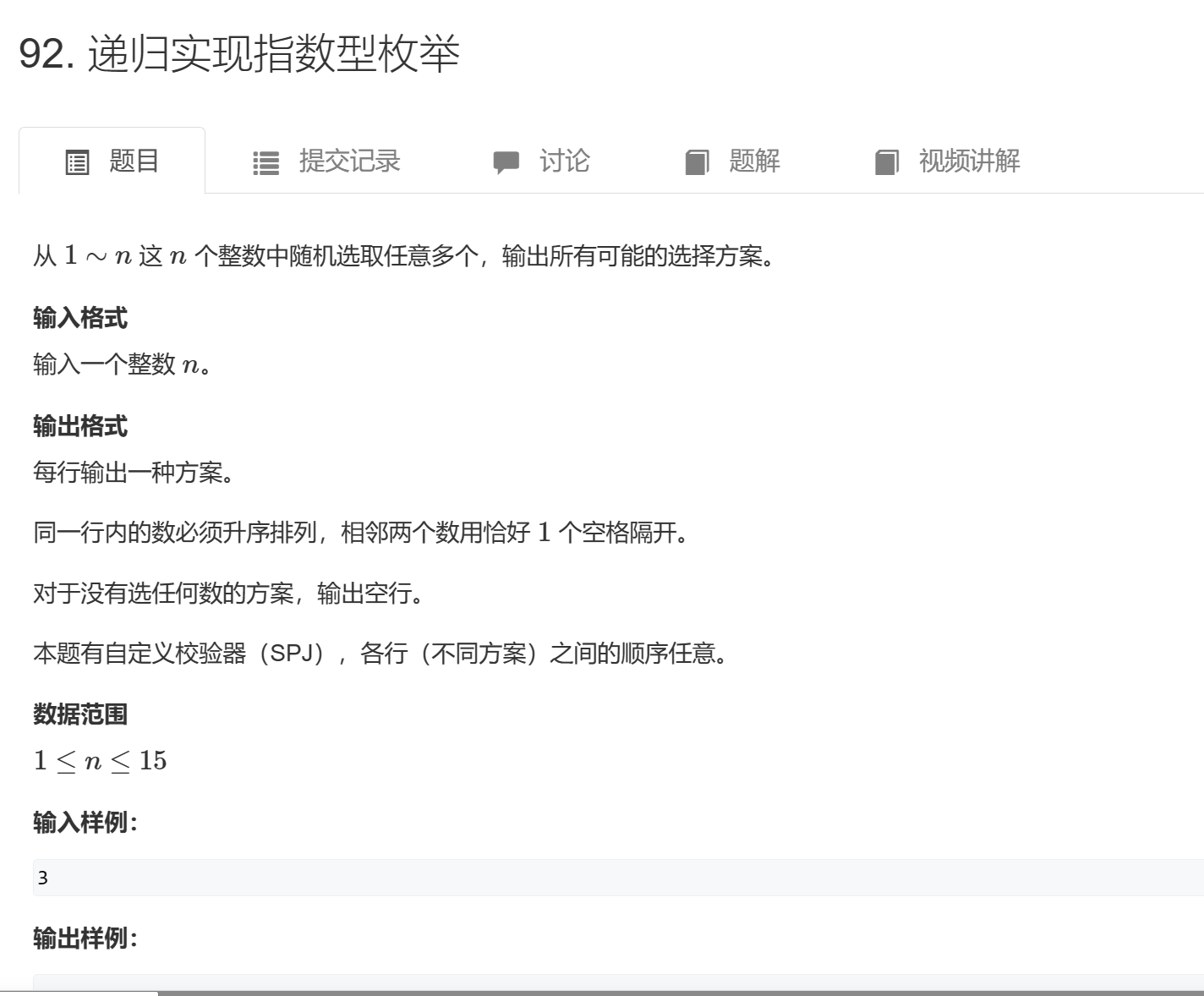
思路:
一、先去确定状态:
阶段就是深度,即选了几个数了
决策就是选与不选,没东西影响决策
开个全局数组记录答案即可
因此状态就是dfs(x)
二、枚举决策:选or不选
三、确定出口:深度>n
Code:
#include <bits/stdc++.h>
#define int long long
const int mxn=3e6+10;
const int mxe=2e5+10;
using namespace std;
vector<int> v;
int n;
int vis[mxn];
void print(){
for(int i=0;i<v.size();i++) cout<<v[i]<<" \n"[i==v.size()-1];
}
void dfs(int u){
if(u>n){
print();
return;
}
v.push_back(u);
dfs(u+1);
v.pop_back();
dfs(u+1);
}
void solve(){
cin>>n;
dfs(1);
cout<<'\n';
}
void init(){}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int __=1;//cin>>__;
init();
while(__--)solve();return 0;
}AcWing 94. 递归实现排列型枚举 - AcWing

一、设状态:
阶段:深度,即选了几个数
影响决策的因素:只能选没选过的数:开个全局vis
记录答案:开个全局数组记录答案
二、枚举决策:
1~n,然后不选vis[i]=1的就行
三、出口:
深度>n
Code:
#include <bits/stdc++.h>
#define int long long
const int mxn=3e6+10;
const int mxe=2e5+10;
using namespace std;
vector<int> v;
int n;
int vis[mxn];
void print(){
for(int i=0;i<v.size();i++) cout<<v[i]<<" \n"[i==v.size()-1];
}
void dfs(int u){
if(u>n){
print();
return;
}
for(int i=1;i<=n;i++){
if(!vis[i]){
v.push_back(i);
vis[i]=1;
dfs(u+1);
vis[i]=0;
v.pop_back();
}
}
}
void solve(){
cin>>n;
dfs(1);
}
void init(){}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int __=1;//cin>>__;
init();
while(__--)solve();return 0;
}93. 递归实现组合型枚举 - AcWing题库
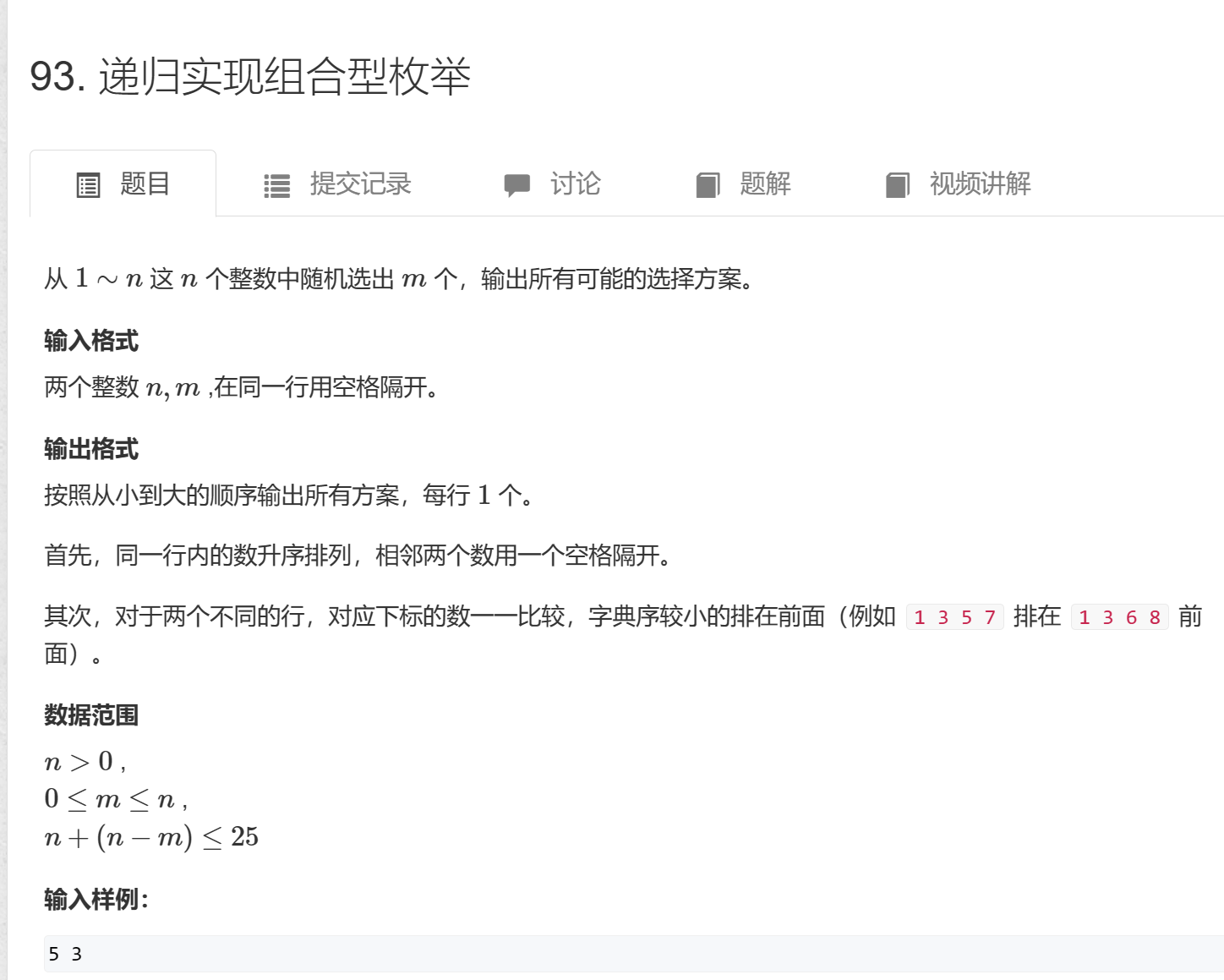
一、确定状态:
阶段:即深度,选不超过m个数
影响决策的因素:每次选比上次选的数大的,因此要记录上次选的数
记录结果:开个全局数组就行了
因此状态就是dfs(u,last),第二维是上次选的数
二、枚举决策:
从last+1开始枚举即可,不用开vis数组,不会重复
三、出口:
选了>m个数
Code:
#include <bits/stdc++.h>
#define int long long
const int mxn=3e6+10;
const int mxe=2e5+10;
using namespace std;
int n,m,len=0;
int vis[mxn],a[mxn];
void print(){
for(int i=1;i<=len;i++) cout<<a[i]<<" \n"[i==len];
}
void dfs(int u,int last){
if(u>m){
print();
return;
}
for(int i=last+1;i<=n;i++){
if(!vis[i]){
vis[i]=1;
a[++len]=i;
dfs(u+1,i);
len--;
vis[i]=0;
}
}
}
void solve(){
cin>>n>>m;
dfs(1,0);
}
void init(){}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int __=1;//cin>>__;
init();
while(__--)solve();return 0;
}AcWing 1209. 带分数 - AcWing
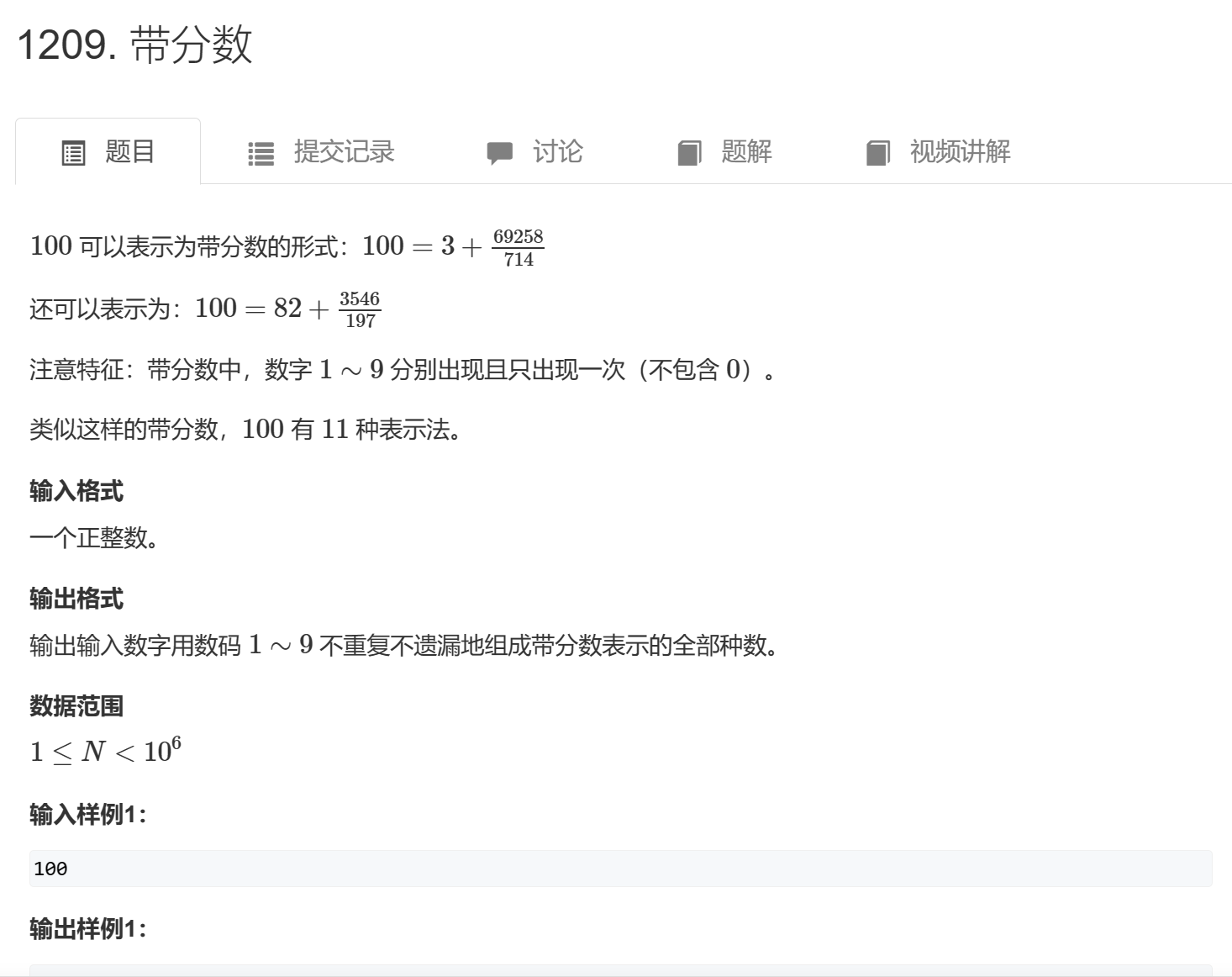
枚举对象:先去枚举全排列,然后枚举两个指针隔起来,验证正确性就好了,不需要dfs爆搜
有个细节就是:不要用substr,写个函数更清晰
Code:
#include <bits/stdc++.h>
//#define int long long
const int mxn=3e6+10;
const int mxe=2e5+10;
using namespace std;
int n;
string s="123456789";
bool check(int x1,int x2,int x3){
if(x2%x3==0&&x1+x2/x3==n) return true;
return false;
}
int trans(int l,int r){
int res=0;
for(int i=l;i<=r;i++){
res=res*10+(s[i]-'0');
}
return res;
}
void solve(){
int ans=0;
cin>>n;
do{
for(int i=0;i<9;i++){
for(int j=i+1;j<9;j++){
int a1=trans(0,i);
int a2=trans(i+1,j);
int a3=trans(j+1,8);
if(a1==0||a2==0||a3==0) continue;
if(check(a1,a2,a3)) ans++;
}
}
}while(next_permutation(s.begin(),s.end()));
cout<<ans<<'\n';
}
void init(){}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int __=1;//cin>>__;
init();
while(__--)solve();return 0;
}AcWing 1208. 翻硬币 - AcWing
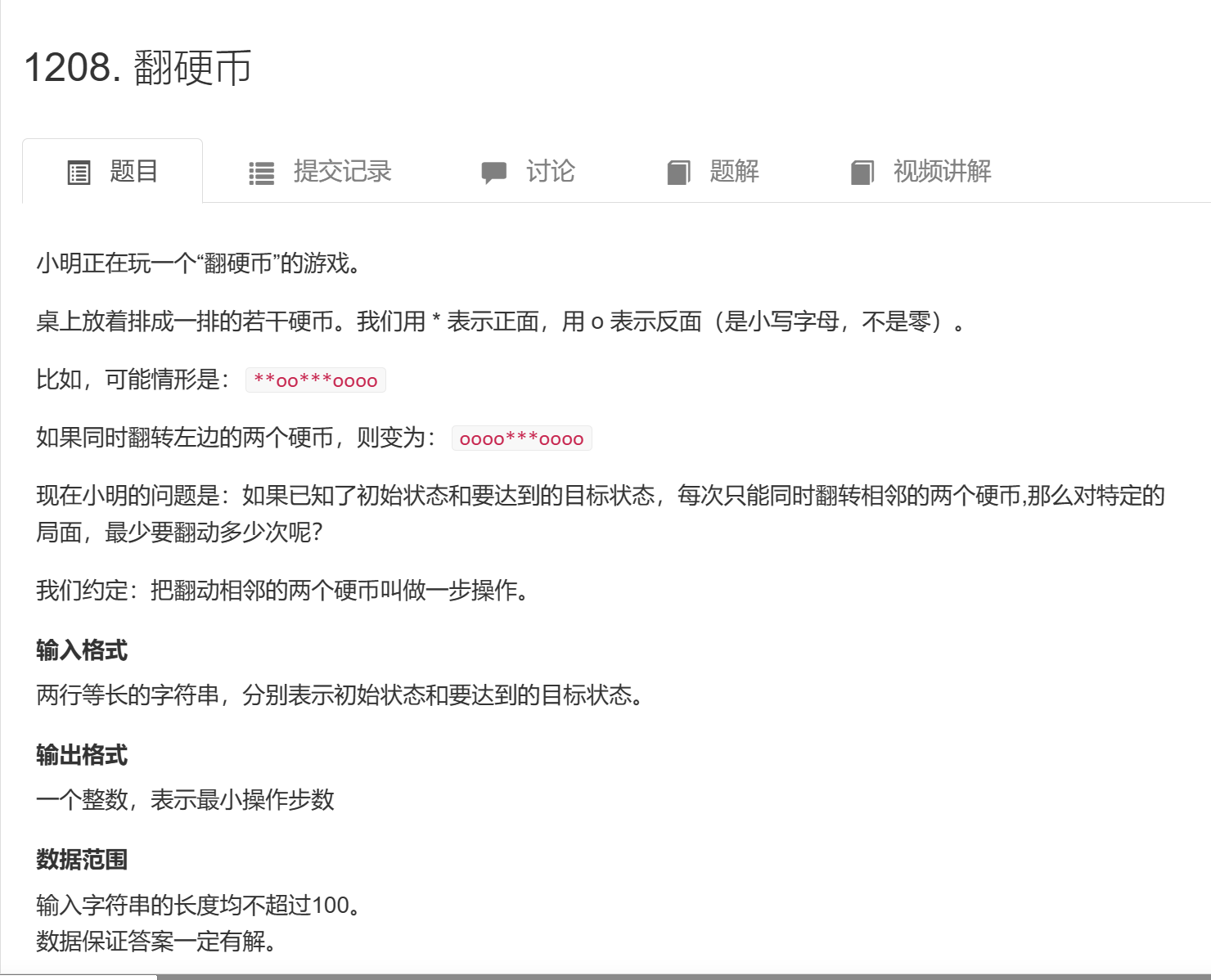
思路:
这是典中典,第一个是确定的,因此只需递推过去就好了
Code:
#include <bits/stdc++.h>
#define int long long
const int mxn=3e6+10;
const int mxe=2e5+10;
using namespace std;
string s,t;
void solve(){
cin>>s>>t;
int cnt=0;
for(int i=0;i<s.size();i++){
if(s[i]!=t[i]){
cnt++;
if(s[i]=='*') s[i]='o';
else s[i]='*';
if(s[i+1]=='o') s[i+1]='*';
else s[i+1]='o';
}
}
cout<<cnt<<'\n';
}
void init(){}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int __=1;//cin>>__;
init();
while(__--)solve();return 0;
}