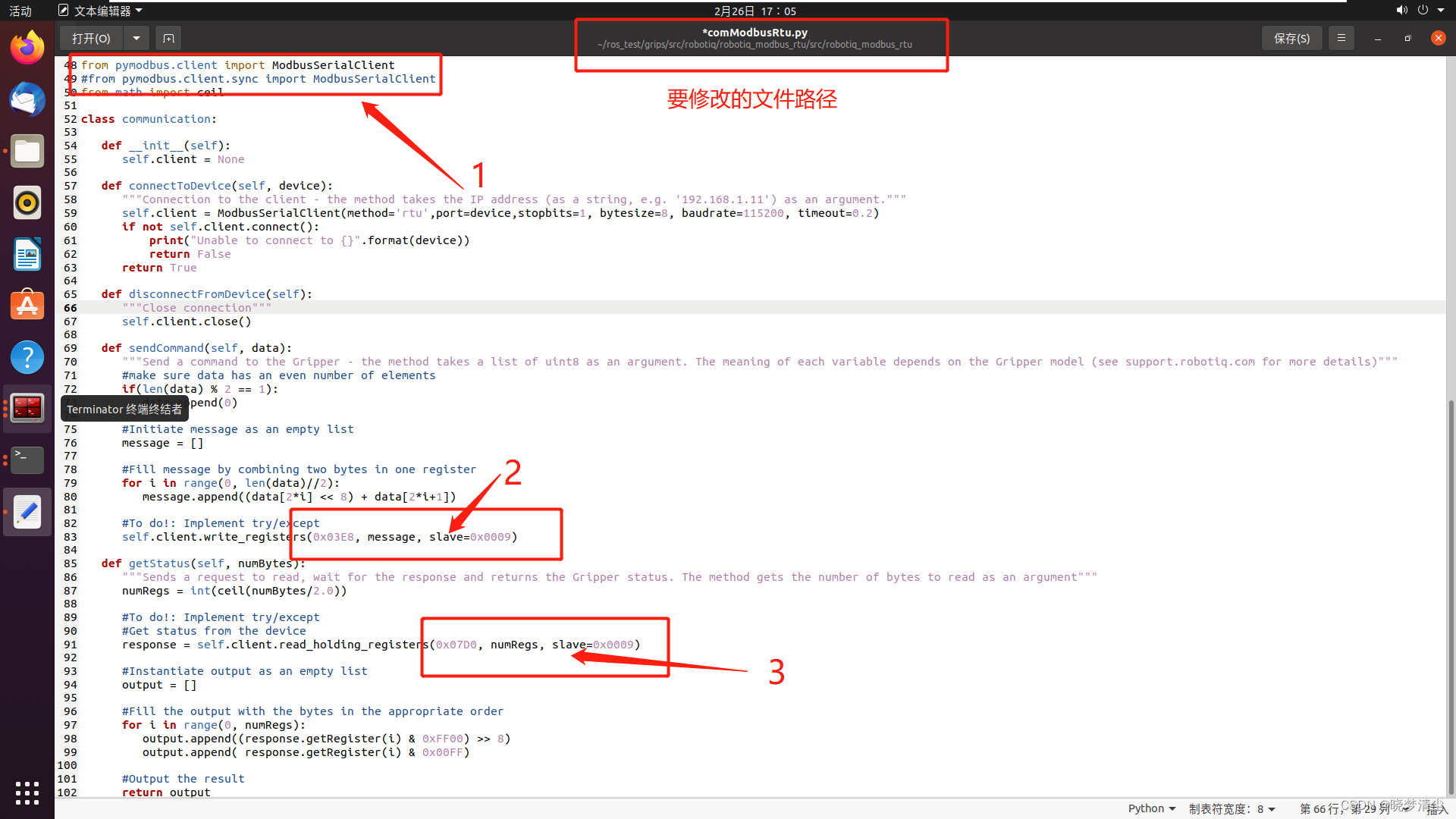
深度学习基础(一) 引入了一个 helloworld，提出了神经网络的简单关系，也就是一个基础公式

a(L) = Sigmoid( a(L-1)*W(L) + b(L))

a(L): 第L层神经元被激活之后 进行Sigmoid函数收敛 得到的值

b(L): 第L层神经元被激活阈值

W(L): 第L层神经元 与 第L-1层神经元之间的关系 权重

由于 神经元之间的关系 通过公式计算之后得到的值 会是一个很大的范围，

我们也无从知道，这个范围多大，总之很多种可能，为了方便操作，采用Sigmoid函数将 计算结果收敛到 0~1 这个范围

从网络第二层开始，每个神经元身上 都具备了n(前一层神经元个数，由于当前层的每个神经元与前一层 的n个神经元都会有关系)个W控制器，1个阈值开关

如此，整个网络就会有很多个 这样的 w b开关，如果这些开关能调试到一个合适的位置，那么整个网络从第一层接收输入的数据，就会吐出来一个不错的结果，比如上篇文章提到的手写体数字识别，得到一个相当不错的识别结果

关键的问题就是，如何调试这些开关，假如有十几二十多个开关，我们还能手动调一调，但 上文中提到的结构，网络有 4层， 784 x 16 x 16 x 10， 总共10000多个开关，这完全不是我们能处理的

神经网络 学习就是 调试这些开关参数了

这篇说文，我不会引入太多的图来说明，主要通过简单的数学逻辑引申到这个主题上来，基本上就是白话了，也没有复杂的公式

如何调试开关

不像我们解微分方程，线性矩阵运算，简单通过微分积分策略与向量方程求解，得到结果就完事了

通过微积分我们能做的那些事，计算机甚至比我们做得更好更高效

主要在于神经网络所阐述的学习逻辑是怎么个逻辑，怎么就能调试那么多的参数

我们在大一都学过 高等数学，想想为什么要求导，我们最开始学习的时候，是怎么引入导数这个概念的，

肯定不是一开始就记公式的，因为要研究一些非线问题，我们通过简单的高中数学无法解决的问题

以一元函数为例，汽车开始行驶 到行驶结束，求速度的问题，还记得那个 小三角变化量么，当时就是为了研究 自变量改变一点点，因变量的变化，引出了导数的概念，然后如何通过积分求面积，就是这样开始的

神经网络也一样，面对庞大的参数集要求解，直接使用公式是没可能的，那么也开始像最开始接触导数一样，从一点点的变化开始慢慢探究

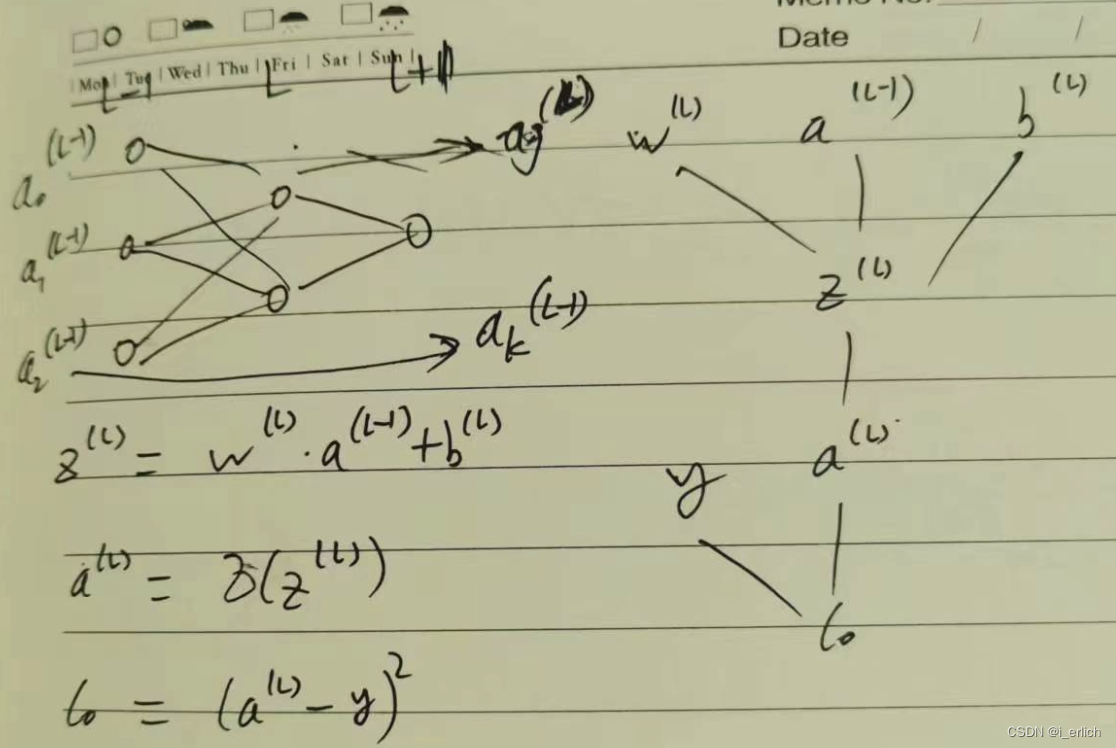
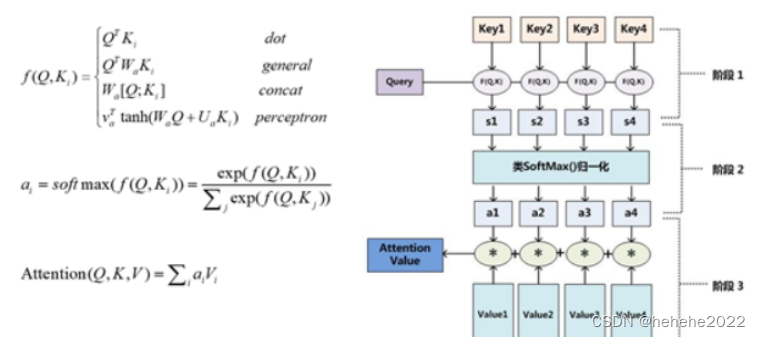
上图就是前面提到的公式了，为了方便理解，引入了变量Z，Sigmoid就是对Z进行收敛

图中的复合多元函数求导也非常简单，用到的链式法则也很好理解，如果确实忘记的话简单百度一下也很容易恢复记忆

神经网络调试开关不是一蹴而就的，而是一点点慢慢调的，这个过程就有点像我们开始学习高等数学解题一样，通过求导慢慢探究，然后通过积分来求面积一样

我们假定神经网络有4层，第一层为输入层，所以第一层神经元 激活值可以认为是确定的

中间两层是通过第一层传递过来的

最后一层为输出层，也是通过中间两层传递输出来的

开始，神经网络给所有的开关随机了一个值作为初始值，当然了，这样网络输出的结果基本上不是我们期望的结果

那就从第一次输出的结果开始，我们能知道输出层与我们期望的结果 相差多少，假定我们是计算机，我们根据结果的偏差来调整我们最后一层神经元上绑定的开关 w，b

这里又不得不插入一些赘述，因为涉及到了结果评价问题，需要对输出结果是什么有直观的认识

---

输出结果其实是 通过输出层的 10个神经元反馈出来的

10个神经元，每个神经元 分别代表着 0，1，2，… 9 这10个罗马数字

每个神经元的激活值 为 0~1，看输出层这10个神经元，谁的 激活值最大，就表示谁代表的罗马数字就是最终的结果

如果 输入的手写体 是个3，那么我们希望神经网络输出的结果自然是3， 代表3的那个神经元的激活值应该最高为1， 其他的神经元激活值应该都为0

这样我们根据结果 判断，目前网络的开关设置下输出的结果与 我们期望得到的结果差别，通过网络最后一层能看到的直观结果就是这样了

---

继续回到调试开关上来

第一次随机开关设置，网络输出之后，我们发现 目标指代正确结果的那个神经元 激活值偏低，非目标神经元激活值偏高

我们当然就希望目标神经元 激活值高一些，非目标神经元 激活值 低一些

如果是这么简单，我们直接调试过来就好了

当然了，这个网络并非输出一种结果，另一组输入，比如手写2，期望输出 2罗马数字，对最后一层开关的调试方案又是一种情况

目前我们的关注点只在最后一层也就是输出层上

神经网络在最后一层上的开关调试，就是 根据各种输入得到的结果偏差，各自期望的调试方向 叠加到一起，形成一个最合适有效的调试方案，最终保障各自的输入都能尽可能的输出正确的结果

正因为，大家都需要调试开关，都有各自的输出诉求，就不能简单粗暴的设置了，需要慢慢商议，你进一点，他退一点，不合适了再反过来，如此，反复磨，反复商议，最终才能形成方案来

---

即使这样，我们也是尽最大可能调试最后一层网络开关而已，中间的两层神经元上也有很多开关，到此我们还未涉及到

码字来说明确实效率有点低下，马上要涉及的神经网络学习策略 放在放在下篇更文