1. fft　傅里叶变换

1.1 傅里叶变换的本质

数学上有一种公式叫做　泰勒展开：

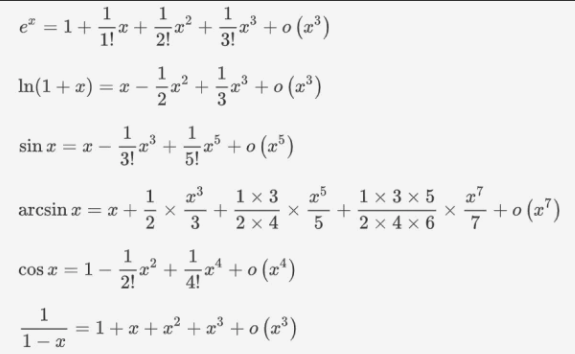
泰勒公式：　其表达的思想，是任意一函数可以有多个指数函数构成

当指数函数的个数趋近于无穷多个，那么组合出来的函数将会逼近原函数；

同样的，　傅里叶想说的，
在信号处理领域，　在时域中，任意一个信号可以由多个正弦信号构成。

在频域中，任意一个信号可以由多个频率分量构成。

1.2　傅里叶变换在时域中的作用

傅立叶变换有助于理解常见的信号，以及如何辨别信号中的错误。 尽管傅立叶变换是一个复杂的数学函数，但是通过一个测量信号来理解傅立叶变换的概念并不复杂。 从根本上说，傅立叶变换将一个信号分解为不同幅值和频率的正弦波。 我们继续来分析这句话的意义所在。
所有信号都是若干正弦波的和

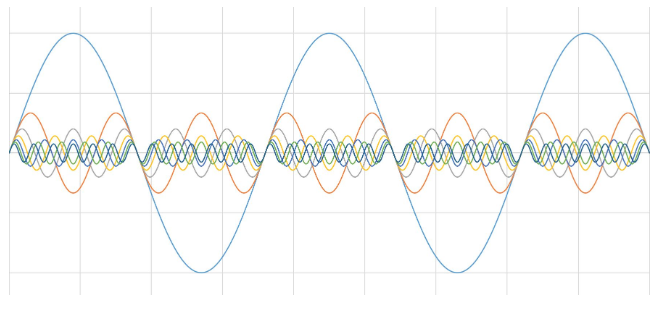
我们通常把一个实际信号看作是根据时间变化的电压值。 这是从时域的角度来观察信号。 傅立叶定律指出，任意波形在时域中都可以由若干个正弦波和余弦波的加权和来表示。 例如，有两个正弦波，其中一个的频率是另一个的3倍。 将两个正弦波相加，就得到了一个不同的信号。

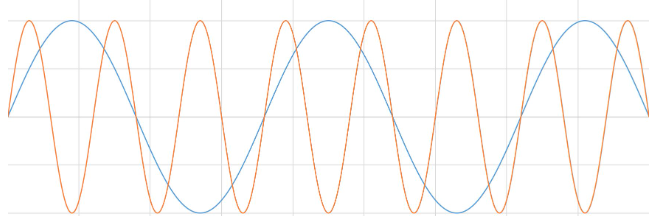
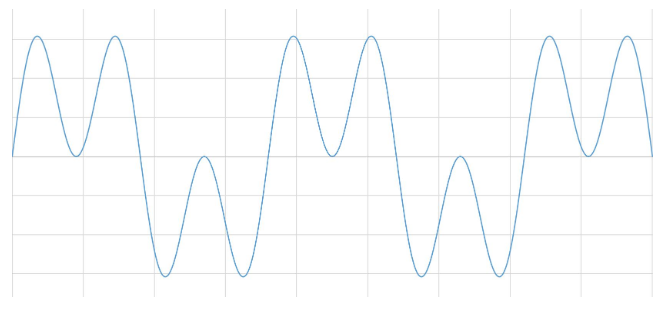
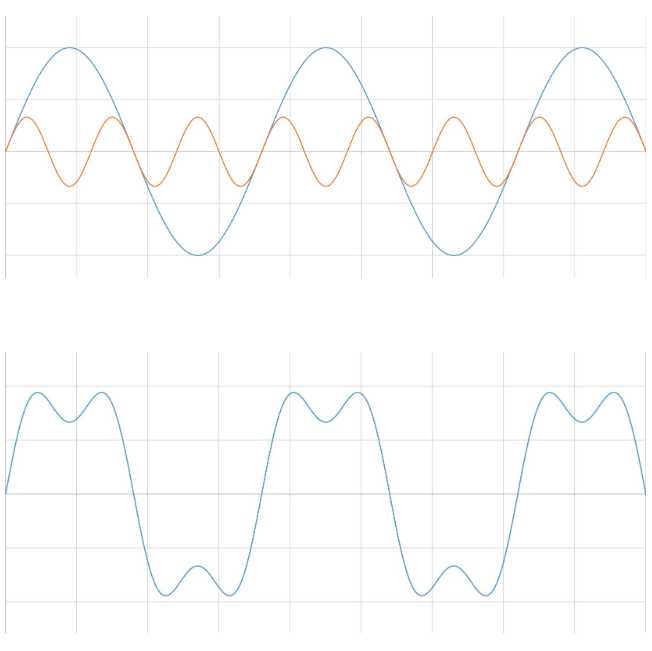
1.3.1 时域中，信号分解的应用

您创建了一个方波。 通过这种方法，所有时域中的信号都可表示为一组正弦波。
即使可以通过这种方法构造信号，那意味着什么呢？ 因为可以通过正弦波构造信号，同理也可以将信号分解为正弦波。 一旦信号被分解，可查看和分析原信号中不同频率的信号。 请参考信号分解的下列使用实例：

• 分解广播信号，可选择要收听的特定频率（电台）。
• 将声频信号分解为不同频率的信号（例如，低音、高音），可增强特定频段，移除噪声。
• 根据速度和强度分解地震波形，可优化楼宇设计，避免强烈震动。
• 分解计算机数据时，可忽略频率重要性最低的数据，这样就能更紧凑地利用内存。这就是文件压缩的原理。

1.3　傅里叶变换在频域中的作用

傅立叶变换将一个时域信号转换为频域信号。 频域信号显示了不同频率对应的电压。 频域是另一种观察信号的角度。

数字化仪对波形进行采样，然后将采样转换为离散的值。 因为发生了转换，傅立叶转换在这些数据上无法进行。 可使用离散傅立叶变换(DFT)，其结果是离散形式的频域信号。 FFT是DFT的一种优化实现，计算量较少，但是本质上是对信号的分解。

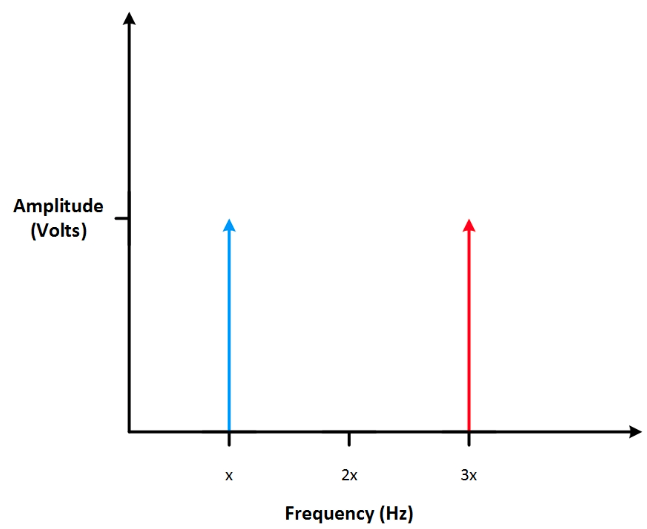
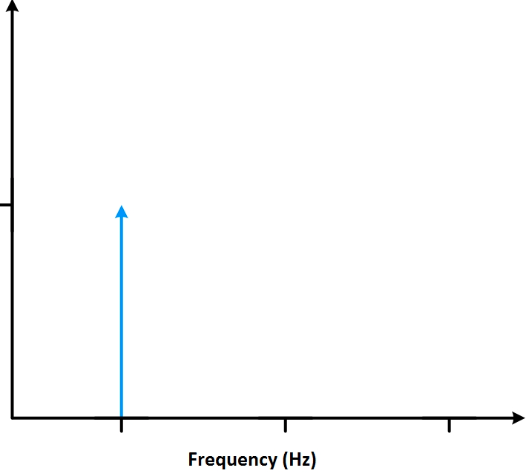
请查看上图1中的信号。 有两个频率不同的信号。在该情况下，频域中就会显示两条表示不同频率的竖线。

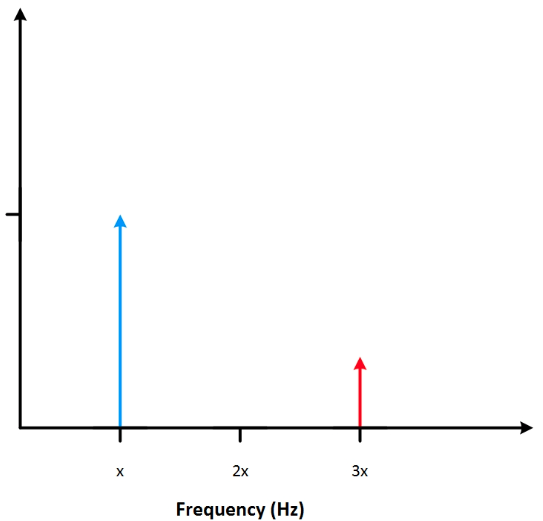
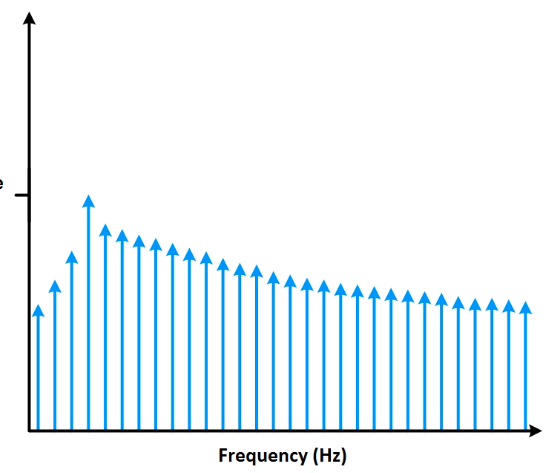
原信号的幅值在竖轴上表示。 图2中有个不同幅值的信号。频域中最高的竖线对应于最高电压的正弦信号。 在频域里观察信号，可直观地看出最高电压发生在哪个频率上。

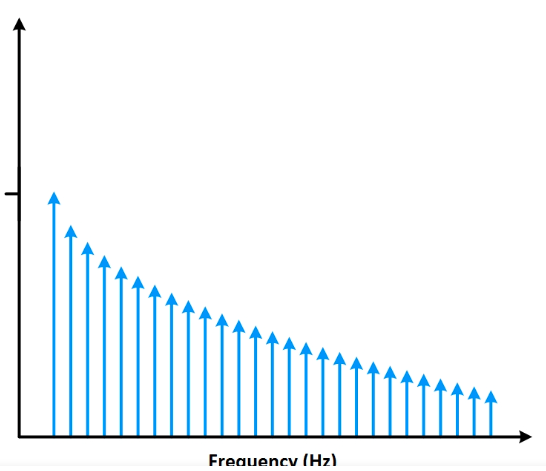
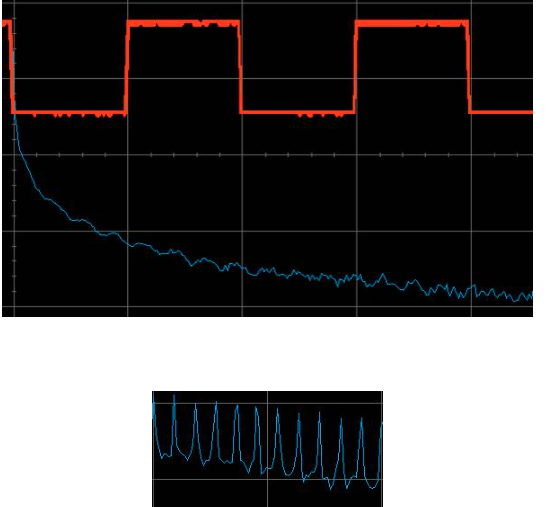
现实生活中，情况是怎样的呢？ 许多混合信号示波器(MSO)都有FFT功能。 下图中，你可以观察到混合信号图中，方波FFT是如何显示的。 放大后可观察到频域中的尖峰。

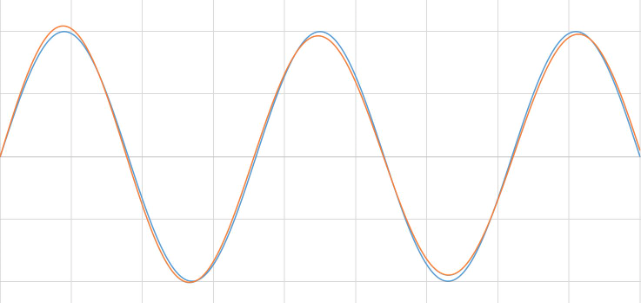
在频域中观察信号有助于验证和发现信号中的问题。 例如，假设有一个输出正弦波的电路。 可在示波器上查看时域输出信号，如图8所示。 看上去没有任何问题！

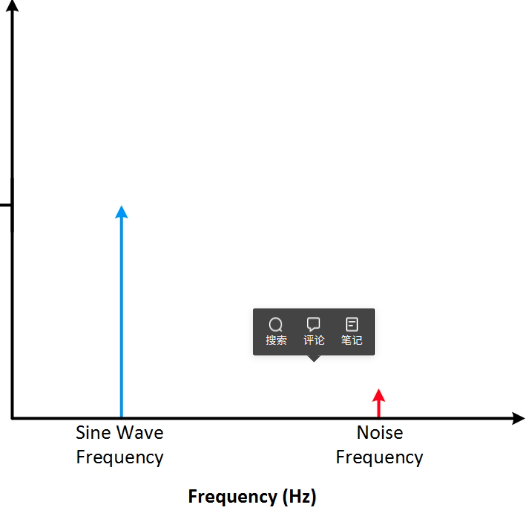
在频域中查看信号时，如果输出的正弦波频率稳定，应该只在频率中显示为一条竖线。 但是，可以看到在更高的频率上仍然有一条竖线，表示正弦波并不如观察到的那么完美。 可尝试优化电路，去除特定频率的噪声。 在频域中显示信号有助于发现信号中的干扰、噪声和抖动。

查看图8中看似完美的正弦波，可以看出波形中有一个抖动

2. 信号的分帧

3. 信号的加窗

FT提供了观察信号的新视角，但是FFT也有各种限制，可通过加窗增加信号的清晰度。

3.1 加窗的含义

使用FFT分析信号的频率成分时，分析的是有限的数据集合。 FFT认为波形是一组有限数据的集合，一个连续的波形是由若干段小波形组成的。 对于FFT而言，时域和频域都是环形的拓扑结构。时间上，波形的前后两个端点是相连的。 如测量的信号是周期信号，采集时间内刚好有整数个周期，那么FFT的上述假设合理。

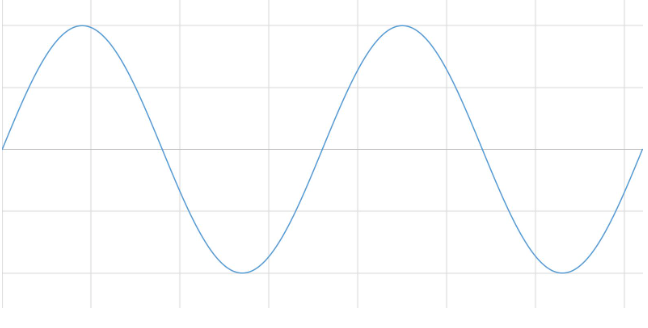
在很多情况下，并不能测量到整数个周期。 因此，测量到的信号就会被从周期中间切断，与时间连续的原信号显示出不同的特征。有限数据采样会使测量信号产生剧烈的变化。 这种剧烈的变化称为不连续性。

采集到的周期为非整数时，端点是不连续的。 这些不连续片段在FFT中显示为高频成分。这些高频成分不存在于原信号中。 这些频率可能远高于奈奎斯特频率，在0～ 采样率的一半的频率区间内产生混叠。 使用FFT获得的频率，不是原信号的实际频率，而是一个改变过的频率。 类似于某个频率的能量泄漏至其他频率。 这种现象叫做频谱泄漏。频率泄漏使好的频谱线扩散到更宽的信号范围中。

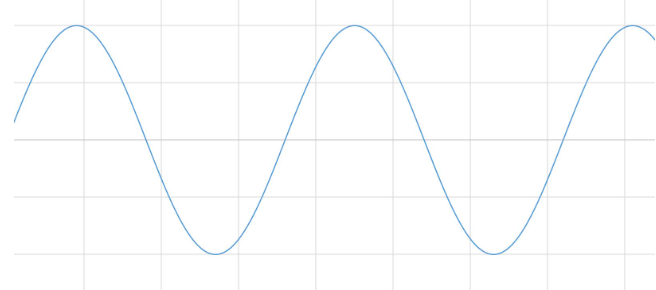
可通过加窗来尽可能减少在非整数个周期上进行FFT产生的误差。 数字化仪采集到的有限序列的边界会呈现不连续性。加窗可减少这些不连续部分的幅值。

加窗包括将时间记录乘以有限长度的窗，窗的幅值逐渐变小，在边沿处为0。 加窗的结果是尽可能呈现出一个连续的波形，减少剧烈的变化。 这种方法也叫应用一个加窗。

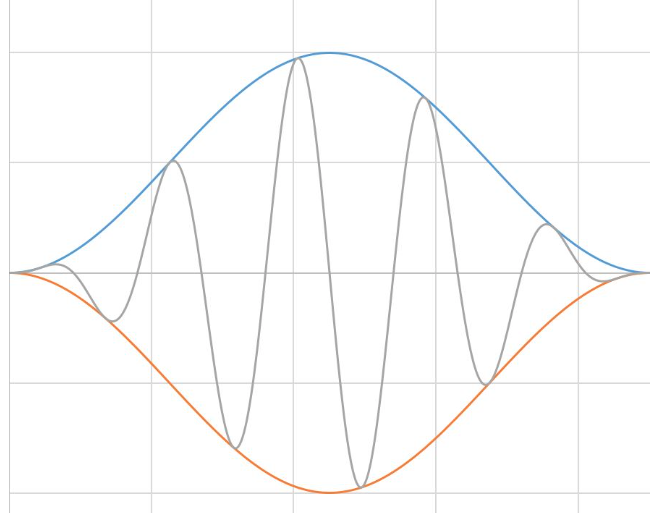
3.2 窗函数的种类

根据信号的不同，可选择不同类型的加窗函数。 要理解窗对信号频率产生怎样的影响，就要先理解窗的频率特性。

窗的波形图显示了窗本身为一个连续的频谱，有一个主瓣，若干旁瓣。 主瓣是时域信号频率成分的中央，旁瓣接近于0。 旁瓣的高度显示了加窗函数对于主瓣周围频率的影响。 对强正弦信号的旁瓣响应可能会超过对较近的弱正弦信号主瓣响应。 一般而言，低旁瓣会减少FFT的泄漏，但是增加主瓣的带宽。 旁瓣的跌落速率是旁瓣峰值的渐进衰减速率。 增加旁瓣的跌落速率，可减少频谱泄漏。

选择加窗函数并非易事。 每一种加窗函数都有其特征和适用范围。 要选择加窗函数，必须先估计信号的频率成分。

如果您的信号具有强干扰频率分量，与感兴趣分量相距较远，那么就应选择具有高旁瓣下降率的平滑窗。

如果您的信号具有强干扰频率分量，与感兴趣分量相距较近，那么就应选择具有低最大旁瓣的窗。

如果感兴趣频率包含两种或多种很距离很近的信号，这时频谱分辨率就非常重要。 在这种情况下，最好选用具有窄主瓣的平滑窗。
如果一个频率成分的幅值精度比信号成分在某个频率区间内精确位置更重要，选择宽主瓣的窗。
如信号频谱较平或频率成分较宽，使用统一窗，或不使用窗。
总之，Hanning窗适用于95%的情况。 它不仅具有较好的频率分辨率，还可减少频谱泄露。 如果您不知道信号特征但是又想使用平滑窗，那么就选择Hanning窗。
即使不使用任何窗，信号也会与高度一致的长方形窗进行卷积运算。本质上相当于对时域输入信号进行截屏，对离散信号也有效。 该卷积有一个正弦波函数特性的频谱。 基于该原因，没有窗叫做统一窗或长方形窗。

Hamming窗和Hanning窗都有正弦波的外形。 两个窗都会产生宽波峰低旁瓣的结果。 Hanning窗在窗口的两端都为0，杜绝了所有不连续性。 Hamming窗的窗口两端不为0，信号中仍然会呈现不连续性。 Hamming窗擅长减少最近的旁瓣，但是不擅长减少其他旁瓣。 Hamming窗和Hanning适用于对频率精度要求较高对旁瓣要求较低的噪声测量。