本篇讲讲八大排序之一的:堆排序 概念复习:
比特数据结构与算法(第四章_上)树和二叉树和堆的概念及结构_GR C的博客-CSDN博客
一、堆排序的概念
堆排序(Heapsort):利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。通过堆来进行选择数据,需要注意的是 排升序要建大堆,排降序建小堆。(易混淆)
排升/降序思路就是建大/小堆,然后把最后一个元素和第一个元素互换,然后把新的最后的一个元素不看作堆内的数据:size-- ; 再向下调整,重复这样,效率就高了。
时间复杂度:O(N*logN)
空间复杂度:O(1)
稳定性:不稳定
二、堆排序的实现
假设我们要对下列数组来使用堆排序:
int arr[ ] = {70, 56, 30, 25, 15, 10, 75};
根据我们之前学到的知识,数组是可以直接看作为完全二叉树的,所以我们可以把它化为堆。此时我们就可以 "选数" (堆排序本质上是一种选择排序)。

第一步:构建堆
第一步就是要想办法把 arr 数组构建成堆(这里我们先排降序构建成小堆)。
构建小堆可以用两种方法,分别为向上调整算法和向下调整算法:
我们这里用向下调整算法,因为等下排序堆的时候也会用到
向下调整算法我们在堆那个章节也学过了,这里我们再来复习一下:
void justDown(int arr[], int sz, int father_idx)
{
int child_idx = father_idx * 2 + 1; // 计算出左孩子的值(默认认为左孩子大)
while (child_idx < sz) // 最坏情況:调到叶子(child_idx >= 数组范围时必然已经调到叶子)
{
if ((child_idx + 1 < sz) && (arr[child_idx + 1] < arr[child_idx]))
{ // 如果右孩子存在且右孩子比左孩子小
child_idx = child_idx + 1;// 让其代表右孩子
}
if (arr[child_idx] < arr[father_idx])//如果孩子的值小于父亲的值(不符合小堆的性质)
{
Swap(&arr[child_idx], &arr[father_idx]);
father_idx = child_idx; // 更新下标往下走
child_idx = father_idx * 2 + 1; // 计算出该节点路线的新父亲
}
else // 如果孩子的值大于父亲的值(符合小堆的性质)
{
break;
}
}
}向下调整算法有一个前提:左右子树必须同为大堆或小堆
如果左子树和右子树不是同一个堆,怎么办?
可以用递归解决,但是我们能用循环就用循环来解决:
叶子所在的子树是不需要调的。所以,我们从倒着走的第一个非叶子结点的子树开始调,然后--。

对30向下调整后变成了 :
70
56 75
25 15 10 30
再--对56向下调整,堆没变
再--对70向下调整,成功变成小堆:
75
56 70
25 15 10 30
//先创建小堆
void HeapSort(int arr[], int sz)
{
int father = ((sz - 1) - 1) / 2; // 计算出最后一个叶子节点(sz-1)的父亲
while (father >= 0)
{
AdjustDown(arr, sz, father);
father--;
}
}测试堆是否创建好了:
#include <stdio.h>
void Swap(int* px, int* py)
{
int tmp = *px;
*px = *py;
*py = tmp;
}
void justDown(int arr[], int sz, int father_idx)
{
int child_idx = father_idx * 2 + 1; // 计算出左孩子的值(默认认为左孩子大)
while (child_idx < sz) // 最坏情況:调到叶子(child_idx >= 数组范围时必然已经调到叶子)
{
if ((child_idx + 1 < sz) && (arr[child_idx + 1] < arr[child_idx]))
{ // 如果右孩子存在且右孩子比左孩子小
child_idx = child_idx + 1;// 让其代表右孩子
}
if (arr[child_idx] < arr[father_idx])//如果孩子的值小于父亲的值(不符合小堆的性质)
{
Swap(&arr[child_idx], &arr[father_idx]);
father_idx = child_idx; // 更新下标往下走
child_idx = father_idx * 2 + 1; // 计算出该节点路线的新父亲
}
else // 如果孩子的值大于父亲的值(符合小堆的性质)
{
break;
}
}
}
//先创建小堆
void HeapSort(int arr[], int sz)
{
int father = ((sz - 1) - 1) / 2; // 计算出最后一个叶子节点的父亲
while (father >= 0)
{
justDown(arr, sz, father);
father--;
}
}
void PrintArray(int arr[], int sz)
{
for (int i = 0; i < sz; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
}
int main()
{
int arr[] = { 70, 56, 30, 25, 15, 10, 75};
int sz = sizeof(arr) / sizeof(arr[0]);
printf("建堆前: ");
PrintArray(arr, sz);
HeapSort(arr, sz);
printf("建堆后: ");
PrintArray(arr, sz);
return 0;
}运行结果:10 15 30 25 56 70 75

第二步:排序
现在堆已经构建完毕了,我们可以开始设计排序部分的算法了。
如果是排升序,建小堆的话:
① 选出最小的数,放到第一个位置,这很简单,直接取顶部就可以得到最小的数。
② 但问题来了,如何选出次小的数呢?
在我们上面的小堆加上几位数:
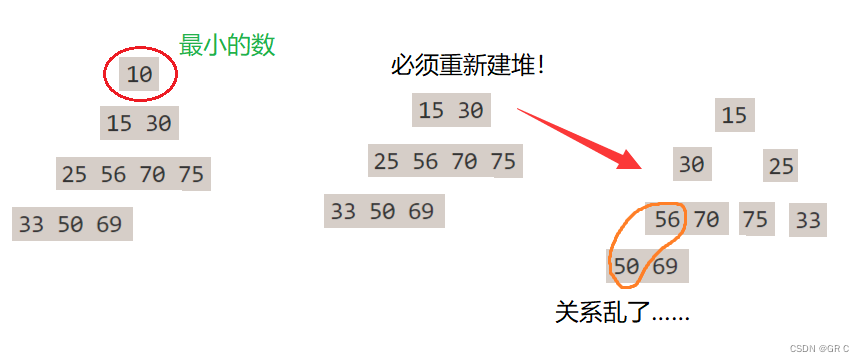
关系乱了还要重新建堆,这样时间复杂度是O(N^2),太慢了
所以我们上面想的是排降序,建小堆,(排升序的话就要建大堆,大于小于号换就行,后面有完整代码)
我们要排降序,我们可以让原来小堆的堆顶数和最后的数进行交换
75
56 70
25 15 10 30
变成
30
56 70
25 15 10 75
这并不会带来堆结构的破坏!我们把75不看作堆的一部分即可。
再进行向下调整,就可以找到次大的数了。此时 时间复杂度为O(N*logN)
这样我们完整的降序HeapSort代码就是
//堆排序 - 降序
void HeapSort(int arr[], int sz)
{
//创建小堆,选出最小的数 O(N)
int father = ((sz - 1) - 1) / 2; // 计算出最后一个叶子节点(sz-1)的父亲
while (father >= 0)
{
justDown(arr, sz, father);
father--;
}
//交换后调堆 O(N * logN)
int end = sz - 1;
while (end > 0)
{
Swap(&arr[0], &arr[end]);
justDown(arr, end, 0);
end--;
}
}降序排序完整代码:
#include <stdio.h>
void Swap(int* px, int* py)
{
int tmp = *px;
*px = *py;
*py = tmp;
}
void justDown(int arr[], int sz, int father_idx)
{
int child_idx = father_idx * 2 + 1; // 计算出左孩子的值(默认认为左孩子大)
while (child_idx < sz) // 最坏情況:调到叶子(child_idx >= 数组范围时必然已经调到叶子)
{
if ((child_idx + 1 < sz) && (arr[child_idx + 1] < arr[child_idx]))
{ // 如果右孩子存在且右孩子比左孩子小
child_idx = child_idx + 1;// 让其代表右孩子
}
if (arr[child_idx] < arr[father_idx])//如果孩子的值小于父亲的值(不符合小堆的性质)
{
Swap(&arr[child_idx], &arr[father_idx]);
father_idx = child_idx; // 更新下标往下走
child_idx = father_idx * 2 + 1; // 计算出该节点路线的新父亲
}
else // 如果孩子的值大于父亲的值(符合小堆的性质)
{
break;
}
}
}
//完整堆排序_降序
void HeapSort(int arr[], int sz)
{
//创建小堆,选出最小的数,时间:O(N)
int father = ((sz - 1) - 1) / 2; // 计算出最后一个叶子节点的父亲
while (father >= 0)
{
justDown(arr, sz, father);
father--;
}
//交换后调堆 时间:O(N * logN)
int end = sz - 1;
while (end > 0)
{
Swap(&arr[0], &arr[end]);
justDown(arr, end, 0);
end--;
}
}
void PrintArray(int arr[], int sz)
{
for (int i = 0; i < sz; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
}
int main()
{
int arr[] = { 70, 56, 30, 25, 15, 10, 75 };
int sz = sizeof(arr) / sizeof(arr[0]);
printf("排序前: ");
PrintArray(arr, sz);
HeapSort(arr, sz);
printf("排序后: ");
PrintArray(arr, sz);
return 0;
}升序排序完整代码:
(上面的justDown改几个大于号小于号就行)
HeapSort函数是一样的,逻辑不一样而已
#include <stdio.h>
void Swap(int* px, int* py)
{
int tmp = *px;
*px = *py;
*py = tmp;
}
void justDown(int arr[], int sz, int father_idx)
{
int child_idx = father_idx * 2 + 1; // 计算出左孩子的值(默认认为左孩子大)
while (child_idx < sz) // 最坏情況:调到叶子(child_idx >= 数组范围时必然已经调到叶子)
{
if ((child_idx + 1 < sz) && (arr[child_idx + 1] > arr[child_idx]))
{ // 如果右孩子存在且右孩子比左孩子大
child_idx = child_idx + 1;// 让其代表右孩子
}
if (arr[child_idx] > arr[father_idx])//如果孩子的值大于父亲的值(不符合大堆的性质)
{
Swap(&arr[child_idx], &arr[father_idx]);
father_idx = child_idx; // 更新下标往下走
child_idx = father_idx * 2 + 1; // 计算出该节点路线的新父亲
}
else // 如果孩子的值小于父亲的值(符合大堆的性质)
{
break;
}
}
}
//完整堆排序_升序
void HeapSort(int arr[], int sz)
{
//创建大堆,选出最大的数,时间:O(N)
int father = ((sz - 1) - 1) / 2; // 计算出最后一个叶子节点的父亲
while (father >= 0)
{
justDown(arr, sz, father);
father--;
}
//交换后调堆 时间:O(N * logN)
int end = sz - 1;
while (end > 0)
{
Swap(&arr[0], &arr[end]);
justDown(arr, end, 0);
end--;
}
}
void PrintArray(int arr[], int sz)
{
for (int i = 0; i < sz; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
}
int main()
{
int arr[] = { 70, 56, 30, 25, 15, 10, 75 };
int sz = sizeof(arr) / sizeof(arr[0]);
printf("排序前: ");
PrintArray(arr, sz);
HeapSort(arr, sz);
printf("排序后: ");
PrintArray(arr, sz);
return 0;
}三、证明建堆的时间复杂度
因为堆是完全二叉树,而满二叉树也是完全二叉树。此处为了简化,将采用满二叉树来证明。
(时间复杂度本来看的就是近似值,所以多几个节点不会影响最终结果):

本篇完。
下一篇:利用堆解决Topk问题