题目描述

原题链接：1143. 最长公共子序列

题目描述

本题和 718. 最长重复子数组（动态规划） 的区别在于此时不要求令一个数组中元素连续。

• 动态规划五步曲：

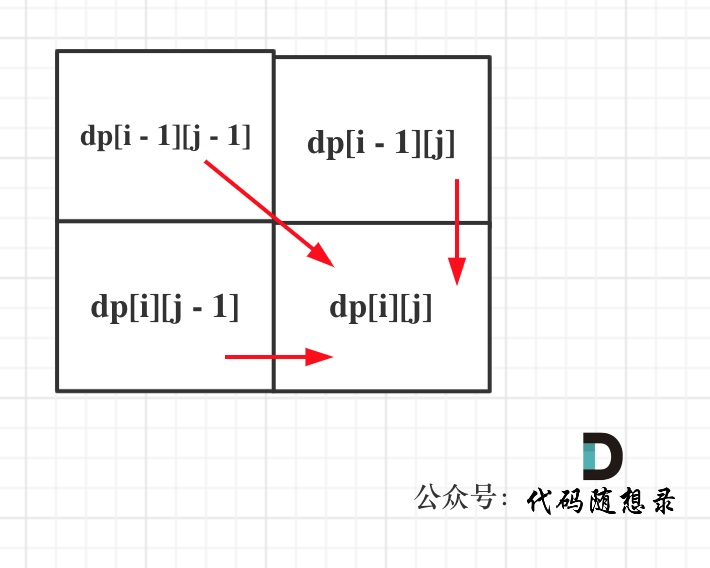
（1）dp[i][j]含义： 截止到text1[i - 1]和text2[j - 1]时，具有的最长公共子序列。

（2）递推公式： 当text1[i - 1] == text2[j - 1]时，令dp[i][j] == dp[i - 1][j - 1] + 1，在上一个长度的基础上加一。不相等时，令dp[i][j] = max(dp[i][j - 1], dp[i - 1][j])，因为i-1和j-1时不等，
则缩小一个第一个的长度和第二个比或缩短一个第二个的长度和第一个比，取二者中的最大长度值。

（3）dp数组初始化： dp[i][0] = dp[0][j] = 0

（4）遍历顺序： 从小到大。

（5）举例：

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int n1 = text1.size(), n2 = text2.size();
        vector<vector<int>> dp(n1 + 1, vector<int>(n2 + 1));
        for(int i = 1; i <= n1; i++) {
            for(int j = 1; j <= n2; j++) {
                if(text1[i - 1] == text2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }

        return dp[n1][n2];
    }
};

参考文章：1143. 最长公共子序列