快速读懂网络拓扑图
- 几重常见的网络拓扑
- 总线型拓扑
- 简介
- 优点
- 缺点
- 环型拓扑
- 简介
- 优点
- 缺点
- 星型拓扑
- 简介
- 优点
- 缺点
- 网络层级机构
- 节点
- 结点
- 链路
- 通路
- 不同的连接线代表什么意思?
- 不同颜色、粗细的直线代表什么意思?
- 闪电线-串行链路
几重常见的网络拓扑
总线型拓扑
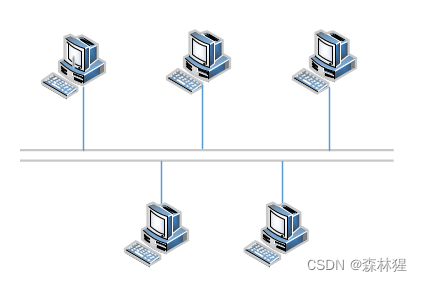
简介
总线型拓扑是采用单根传输作为共用的传输介质,将网络中所有的计算机通过相应的硬件接口和电缆直接连接到这根共享的总线上。使用总线型拓扑结构需解决的是确保端用户使用媒体发送数据时不能出现冲突。
优点
(1)网络结构简单,易于网络扩展;
(2)设备少、造价低,安装和使用方便;
(3)具有较高的可靠性。因为单个节点的故障不会涉及整个网络。
缺点
(1)总线传输距离有限,通信范围受到限制;
(2)故障诊断和隔离比较困难。故障隔离困难。当节点发生故障,隔离起来还比较方便,一旦传输介质出现故障时,就需要将整个总线切断;
(3)易于发生数据碰撞,线路争用现象比较严重;
(4)分布式协议不能保证信息的及时传送,不具有实时功能,站点必须有介质访问控制功能,从而增加了站点的硬件和软件开销。
环型拓扑
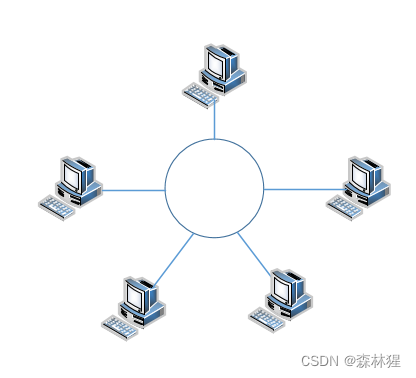
简介
环型拓扑是使用公共电缆组成一个封闭的环,各节点直接连到环上,信息沿着环按一定方向从一个节点传送到另一个节点。环接口一般由发送器、接收器、控制器、线控制器和线接收器组成。在环型拓扑结构中,有一个控制发送数据权力的“令牌”,它在后边按一定的方向单向环绕传送,每经过一个节点都要被接收,判断一次,是发给该节点的则接收,否则的话就将数据送回到环中继续往下传。
优点
(1)电缆长度短,只需要将各节点逐次相连。
(2)可使用光纤。光纤的传输速率很高,十分适合于环形拓扑的单方面传输。
(3)所有站点都能公平访问网络的其他部分,网络性能稳定。
缺点
(1)节点故障会引起全网故障,是因为数据传输需要通过环上的每一个节点,如某一节点故障,则引起全网故障。
(2)节点的加入和撤出过程复杂。
(3)介质访问控制协议采用令牌传递的方式,在负载很轻时信道利用率相对较低。
星型拓扑
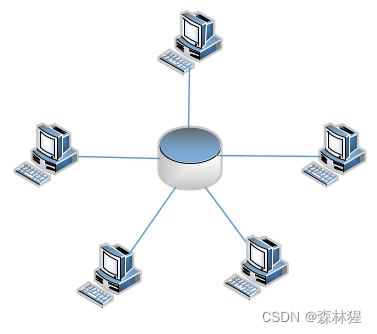
简介
星型拓扑结构的网络属于集中控制型网络,整个网络由中心节点执行集中式通行控制管理,各节点间的通信都要通过中心节点。每一个要发送数据的节点都将要发送到数据发送中心节点,再由中心节点负责将数据送到目地节点。因此,中心节点相当复杂,而各个节点的通信处理负担都很小,只需要满足链路的简单通信要求。
优点
(1)控制简单。任何一站点只和中央节点相连接,因而介质访问控制方法简单,致使访问协议也十分简单。易于网络监控和管理。
(2)故障诊断和隔离容易。中央节点对连接线路可以逐一隔离进行故障检测和定位,单个连接点的故障只影响一个设备,不会影响全网。
(3)方便服务。中央节点可以方便地对各个站点提供服务和网络重新配置,建网容易。
缺点
(1)需要耗费大量的电缆,安装、维护的工作量也骤增。
(2)中央节点负担重,形成“瓶颈”,一旦发生故障,则全网受影响。
(3)各站点的分布处理能力较低。
网络层级机构
标准的三层结构:核心层,汇聚层,接入层
如果网络规模不大的话,可以把汇聚层省略掉,变成核心层和接入层。
节点
一个“节点”其实就是一个网络端口。节点又分为“转节点”和“访问节点”两类。“转节点”的作用是支持网络的连接,它通过通信线路转接和传递信息,如交换机、网关、路由器、防火墙设备的各个[网络端口]等;而“访问节点”是信息交换的源点和目标点,通常是用户计算机上的网卡接口。如我们在设计一个网络系统时,通常所说的共有××个节点,其实就是在网络中有多个要配置IP地址的网络端口。
转自:https://www.jianshu.com/p/352faaae6291
结点
一个“结点”是指一台网络设备,因为它们通常连接了多个“节点”,所以称之为“结点”。在计算机网络中的结点又分为链路结点和路由结点,它们就分别对应的是网络中的交换机和路由器。从网络中的结点数多少就可以大概知道你的计算机网络规模和基本结构了。
转自:https://www.jianshu.com/p/352faaae6291
链路
“链路”是两个节点间的线路。链路分物理链路和逻辑链路(或称数据链路)两种,前者是指实际存在的通信线路,由设备网络端口和传输介质连接实现;后者是指在逻辑上起作用的网络通路,由计算机网络体系结构中的数据链路层标准和协议来实现。如果链路层协议没有起作用,数据链路也就无法建立起来。
转自:https://www.jianshu.com/p/352faaae6291
通路
“通路”从发出信息的节点到接收信息的节点之间的一串节点和链路的组合。也就是说,它是一系列穿越通信网络而建立起来的节点到节点的链路串连。它与“链路”的区别主要在于一条“通路”中可能包括多条“链路”。
转自:https://www.jianshu.com/p/352faaae6291
不同的连接线代表什么意思?
1.两条直线,中间一个椭圆
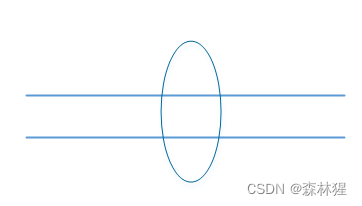
含义:两根线上加个圆圈表示这两根线是处于聚合状态,也就是说把两根线绑定在一起使用,目的是为了增加链路带宽。
圆圈表示将两个物理链路捆绑为一个逻辑链路的意思。既增加了带宽,又有了保障,即一个断掉,另外一个还能用,平时两个是一起用的
使用场景*:双路冗余部署的交换机、网络设备之间,可采用此方式连接。
不同颜色、粗细的直线代表什么意思?

闪电线-串行链路

含义:串行链路,用于两个路由器之间的连接,连接两个路由器的串口。
使用场景:通常用于两个网之间的连接。比如内网和互联网之间。