二分法
二分法非常让我们头痛,不论对于初学者,还是对于有一定编程经验的人来讲,我们都会以为这个思想很简单,而不去在意,可是在实际运用中我们在处理边界条件的时候,往往会要不写出了死循环,要不就会发生数组越界,或者说不知道最终搜索结束的时候结果究竟在哪里为什么有的时候是 left = mid+1 有的时候是 left =mid ,在写的时候尽管很小心考虑了边界情况可是还是会出现错误,那么下面的介绍会让你豁然开朗,作者本人也是经过了很多人写的二分版本,下面会给3种二分版本,一种比较好理解,作为我们日常使用,剩余两种用于我们的知识拓展
前题引入 : 在高中我们学过如何进行找到快速找到线路断的点,在一个有一个断电的节点在一个很长的电线上
我们如何快速的找到这个点在什么地方,我们在任意一端通电,去量中点是否有电如果有电位的话就是另一半出了故障点,
接下来继续在有故障的半段接着我们刚才的操作后,有故障的区间会越来越小,在经过log2N次后我们就可以找到故障的点。
我们在一个有序数组查找某一个固定的值,或者说具有二段性(可以根据一个值来将整个数组或者数组的局部来分成两半),而题目中还要求我们写时间复杂度为O(log n)级别的算法,我们第一考虑必然是二分法。
题目链接:
704.二分查找
34. 在排序数组中查找元素的第一个和最后一个位置
74. 搜索二维矩阵
153. 寻找旋转排序数组中的最小值
剑指 Offer 11. 旋转数组的最小数字
33. 搜索旋转排序数组
162. 寻找峰值
题目由容易到难,由普通的二分查找,到特殊的二分查找,到二分查找的变式,可以按着顺序做的,注意第4个题和第五个题不一样,二分法的二段性可以在这两个题中显现出来,不要看着像就不去做了哦,要仔细分析他为什么错,当然我们可以根据他报错的测试用例来进行筛选写出来,但是如果我们不知道原理的话下次还是很难写出来的。
二分法第一种模板(十分推荐)
下面来给出代码,然后在解释原因,这边只是举了一个升序的例子,下面对于具体问题还是得来具体分析,建议上来不要直接看代码,先看原因,如果比较熟练可以直接看代码。
// 假设数组长度为 N,长度题目会给出,这边用一个宏写代码时不会报错看着舒服一点。
// 数组长度为N,数组的有效下标 0~N-1
#define N 100
int find(int *arr,int target)
{
int left = -1; //左边界
int right = N ; //右边界
while(left + 1 != right )
{
// 防止 left + right 会超过 int 所能表示的范围
// 化简后和 ( left + right ) / 2 没有区别
int mid = left + ( right - left ) / 2;
if(arr[mid] >= target )
{
right = target ;
}else
{
left = target;
}
}
// 返回-1表示target不在该数组中,这里判断防止我们接下来返回的时候发生越界,
// 我们if判断的时候等于是包在右边界的,我们应该在右边界返回结果,但是当target的值大于数组的最大值的时候
// left = N-1,right = N ,在我们回收结果的时候会发生越界
if(right == N)
{
return -1;
}
return arr[right]==target ? right : 1;
}
会让我们纠结的是下面几个点
left = ?
right = ?
while(?)
{
int mid = left + ( right - left ) / 2;
if(?)
{
}else
{
}
}
// 过滤操作怎么写
return ?;
这些问号的所在地经常是我们会让程序出现错误的地方
为什么要这么写
一个bilibili up主的视频教学
如果有侵权联系我,马上会进行删除
我们一定要了解二分法的思想,不然在遇到变式的时候我们还是一头雾水,耐心看完
边界思想,gif可能有点慢。
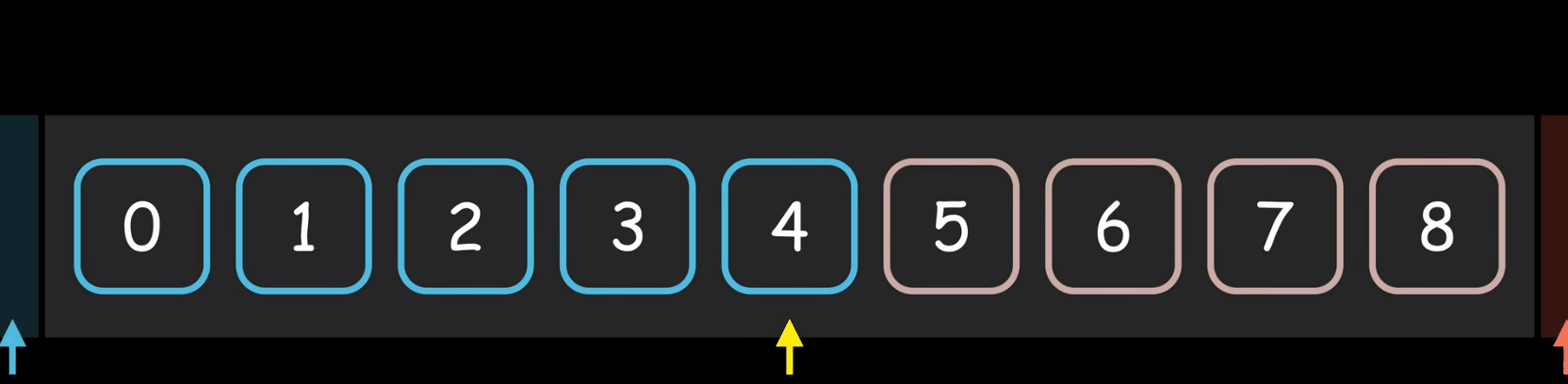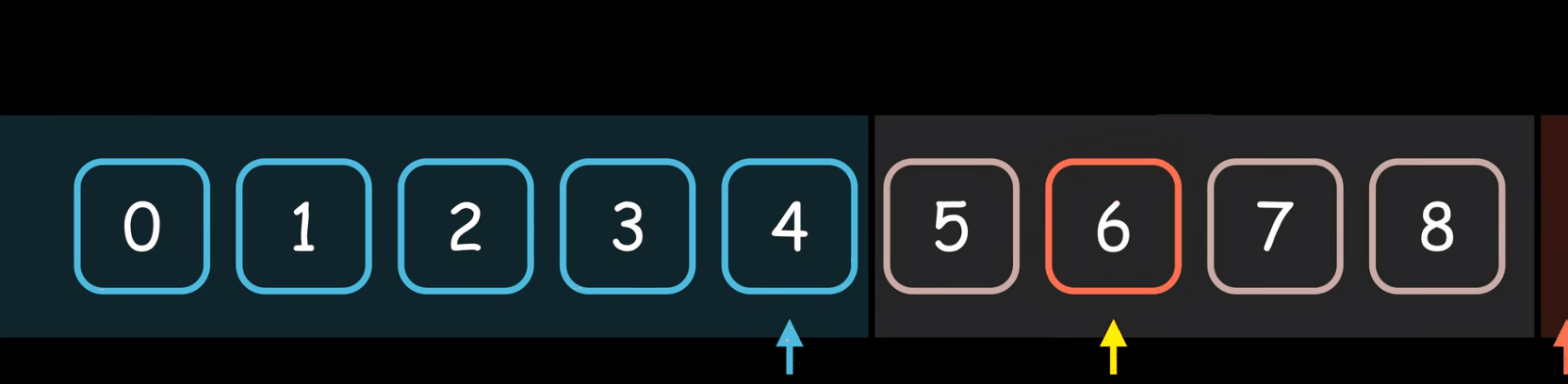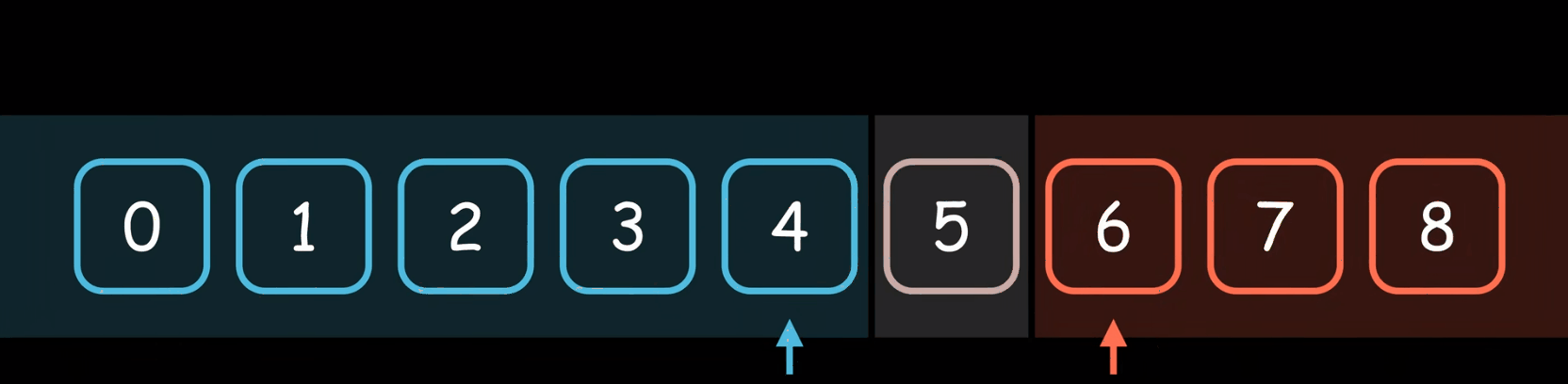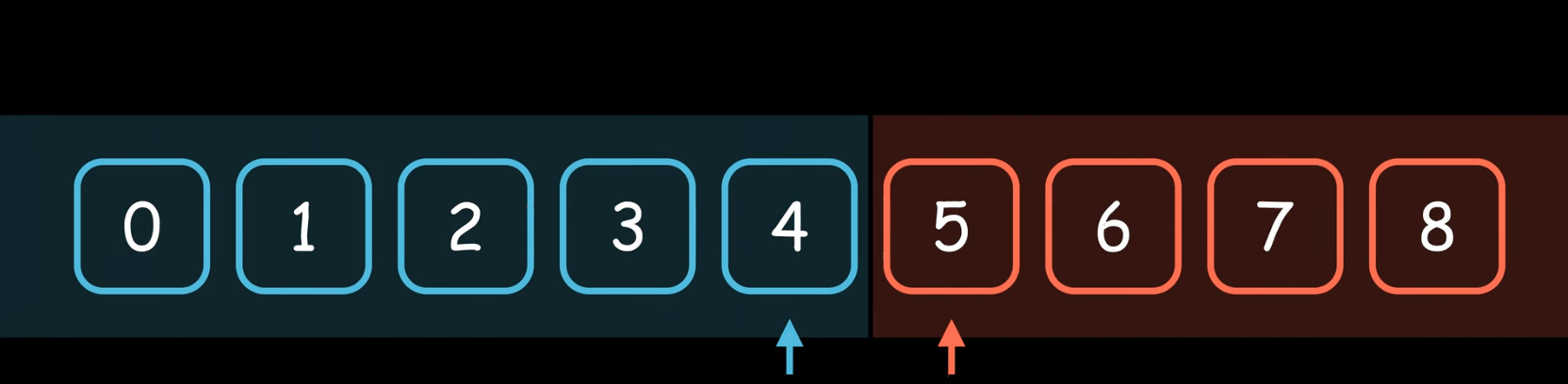
这里我们把二分查找的过程想象成边界的扩充,我们给他一个条件,他把满足条件的边界在左边,不满足条件的在右边,那么我们在开始的时候因为我们不知道第一个值或者最后一个值是不是满足我们的条件,我们没法把边界直接设置到left = 0、right = N-1。
以上面有序升序数组找target升序数组中有没有重复值无所谓,如果找到我们返回他的下标,如果找不到我们返回-1。如果我们把left左边理解为是<= target的,右边界是 >target的注意不能在等于了(但是如果想要这里要等于前面就不能要了,下面会详细解释接着看),如果数组中的所有的值都小于arr[0],那么右边界在循环结束后应该是right == 0的才满足我们边界的定义,而left不能等于0,因为0位置也是大于我们的target的值的,那么如果所有的值都大于我们的arr[N-1]的时候,按照我们边界的定义循环结束后left == N-1,因为这个时候arr[N-1]不满足我们的右边界的定义,所以一开始的时候我们能让right =N-1;
所以我们 left right应该是下面的写法
left = -1;
right = N;
如果按照边界的思想,那么到最后的时候左边界应该和右边界相邻,所以我们循环的条件为
while(left + 1 != left)
如果我们按照边界思想,那么我们每次在与arr[mid]比较的时候,我们可以把等于的放到左边中间的值已经比较所以我们把这个条件放到左边界,或者直接放到右边界,不过接收的值需要根据我们的条件而定
// 第一种写法
// 显然左边界的值都小于等于 target,而数组又是有序的
// 那么如果该数组中有target左边界的值就等于target,如果没有左边界的值就会直接等于target
// 所以我们在循环结束对arr[left]的值进行判断就可以了
if(arr[left] <= target)
{
left = mid;
}else
{
right = mid;
}
// 第二种写法思路和第一种一样不过写法不一样
if(arr[left] >= target)
{
right = mid;
}else
{
left = mid;
}
在循环结束后,我们要考虑极端情况,就是目标值比数组中所有的都大,或者比数组中所有的值都小这种情况,因为我们定义边界的时候,我们的边界初始化的值是一个超出数组边界的一个边界值,不进行判断的话有可能会发生错误
- 检查索引是否越界
- 检查我们的边界值是否等于我们的目标值
// 如果我们是这一种写法的话
// target的值小于我们数组中的每一个值的的情况下
// 我们循环结束后 left = -1 right =0
while(left +1 !=right)
{
if(arr[left] <= target)
{
left = mid;
}else
{
right = mid;
}
}
//循环结束后进行判断
//1.
if(left == -1)
{
return -1;
}
//2.
if(arr[left] == target)
{
return left;
}else
{
return -1;
}
// 如果target大于我们的数组中的每一个值
// 我们循环结束后 left = N-1 也就是数组的最后一个元素
// right = N
while(left + 1 != right )
{
if(arr[left] >= target)
{
right = mid;
}else
{
left = mid;
}
}
// 循环结束后进行判断
// 1.
if(right == N)
{
return -1;
}
//2.
if(arr[right] == target)
{
return right
}
else
{
return -1;
}
二分法的其他两种模板(拓展知识面)
代码随想录中的写法
假设 N是数组的长度
int left = 0;
int right = N-1;
// [0,N]
while(left <= right)
{
int mid = left + ( right - left ) / 2;
if(arr[mid] > target)
{
right = mid -1;
}else if(arr[mid] < target)
{
left = mid + 1;
}
else
{
// 等于的情况
return mid;
}
}
// 循环结束后 left 一定是在 right 的后一个位置的
// left == right 那么什么情况会导致 right 和 left 移动呢
// arr[left] > targht arr[right] <target
// 返回主要靠mid 这种方法处理的情况比较单一
int left = 0;
int right = N;
// [0,N)
while(left < right)
{
int mid = left + ( right - left ) / 2;
if(arr[mid] > target)
{
right = mid -1 ;
}else if(arr[mid] < target)
{
left = mid ;
}
else
{
// 等于的情况
return mid;
}
}
```c++
// [0,N)
while(left < right)
{
int mid = left + ( right - left ) / 2;
if(arr[mid] > target)
{
right = mid -1 ;
}else if(arr[mid] < target)
{
left = mid ;
}
else
{
// 等于的情况
return mid;
}
}