我们的目标是构造 zkSNARK。在我们的目标场景中，Prover 只需要发送一个简短的证明字符串给 Verifier，而 Verifier 不需要给 Prover 发送任何消息。

直接构造一个满足这个场景的 zkSNARK 可能会很困难。一个更灵活的方式是在先在理想模型下构造证明系统，然后用一个通用的转换，把这个只能在理想场景下的系统转化成现实场景中可以工作的 zkSNARK。

理想模型中，就是指这个模型用到了场景中并不存在的功能，叫做理想功能。理想功能的存在使得构造证明更加方便。构造好之后，使用密码学工具模拟这个不存在的功能，以实现这个理想模型。

下图是 ZKP 常用的理想模型，以及它们之间的转换关系。接下来我们会一一介绍这些模型以及它们之间的转换的具体实现。

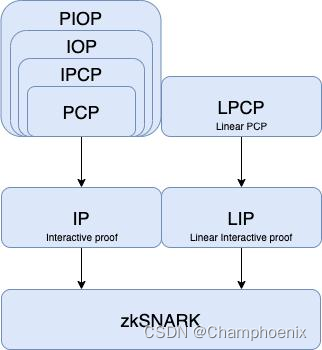
IP

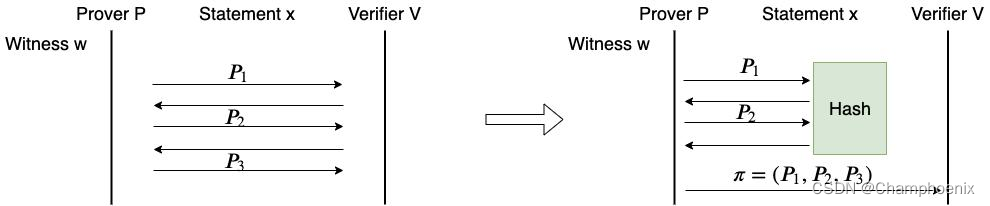
PCP

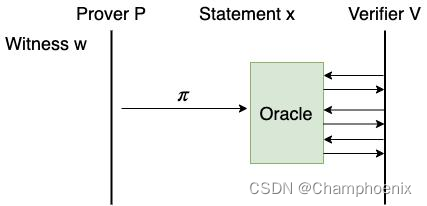
Babai 等人在 1991 年提出了随机可查证明 (Probabilistically Checkable Proof, PCP)。在 PCP 模型中，Prover 构造一个证明字符串，叫做 PCP 证明。PCP 证明的长度可以非常长，远远超过 Verifier 的计算能力。所以，Prover 不会直接把 PCP 证明发送给 Verifier，而是向 Verifier 发送一个预言机 (Oracle)，叫做 PCP 预言机。Verifier 可以随意查询 PCP 预言机，获取 PCP 字符串任意位置的比特。

为了理解 IP 和 PCP 的关系，我们举一个现实中的例子。我们请上我们熟悉的主人公 Alice 和 Bob。假设 Alice 是一名即将毕业的研究生，Bob 的任务是评审 Alice 的课题是否合格。IP 模型就是答辩，Alice 和 Bob 直接对话，如果 Alice 能成功回答 Bob 的所有提问，Alice 就成功毕业了。而在 PCP 模型中，没有答辩，Alice 只是把毕业论文发给 Bob，而毕业论文超级长，Bob 不可能看完论文，只能在论文中随机挑选几段来读，如果挑的这些段落都没有问题，相互之间逻辑通顺，Bob 就相信 Alice 的课题是合格的。

PCP 预言机提供了这样的功能：它本身很短，传递它只需要很小的通信量；它传递的信息量却很大，通过它可以随机访问一个很长的字符串。显然，真正的 PCP 预言机是不存在的，PCP 是一个理想化的模型。

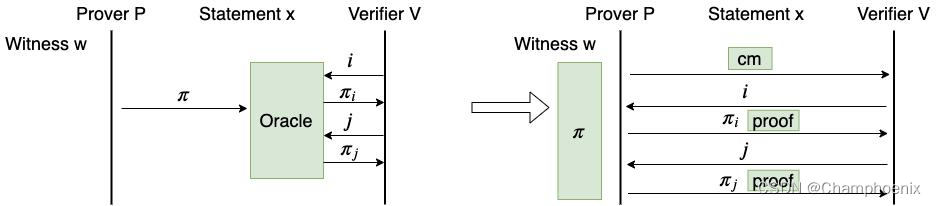
IPCP
IPCP (Interactive PCP) 模型可以看做 IP 模型和 PCP 模型的相加。在 IPCP 模型中，Prover 向 Verifier 发送了 PCP 预言机后，Prover 和 Verifier 继续进行交互。交互过程中，Verifier 可以不时地访问 PCP 预言机。

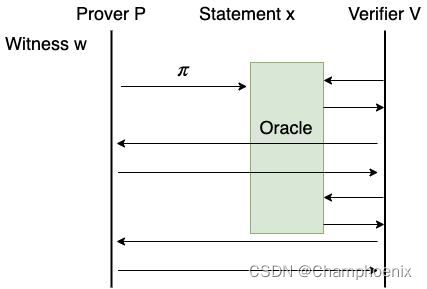
继续使用上一节中 Alice 和 Bob 的例子。如果说 IP 模型是只有答辩，PCP 模型是只有毕业论文，那么 IPCP 模型就是在 Alice 答辩之前把毕业论文发给 Bob。在答辩过程中，Bob 可以一边看毕业论文一边向 Alice 提问。

基于 IPCP 模型构造的证明系统也可以通过 Merkle-Tree 或一般的 VC 方案转化成 IP 模型下的证明系统，过程和 PCP 模型的转换完全一样，区别仅在于，Verifier 在查询 PCP 证明的请求中可能夹杂着普通的交互。

IP 模型和 PCP 模型都可以看做是特殊的 IPCP 模型。其中，IP 模型相当于在 IPCP 模型中 Prover 发送一个空预言机给 Verifier。PCP 模型相当于在 IPCP 中省略掉 Prover 和 Verifier 的对话环节。

IOP

如果说 IPCP 模型是把 IP 和 PCP 模型做加法，那么 IOP (Interactive Oracle Proof) 模型就是把 IP 和 PCP 做乘法。在 IOP 模型中，Verifier 向 Prover 发送消息，而 Prover 则向 Verifier 发送 PCP 预言机。Verifier 可以随意查询 Prover 发过的任何 PCP 预言机。

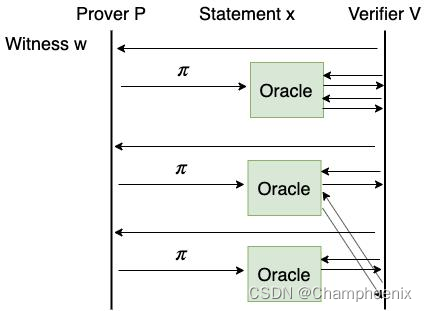
继续使用前面 Alice 和 Bob 的例子来解释 IOP 模型。Alice 把毕业论文发给 Bob，Bob 给 Alice 回复一个简短的评论意见，然后 Alice 再写一篇论文发给 Bob，Bob 再回复，这样来回进行多次。这个过程中，Bob 可以随时阅读 Alice 发给过他的任何一篇论文，当然 Bob 的时间仍然不够，Bob 仍然只能随机选取一小部分阅读。最后，Bob 判断 Alice 的课题是否合格。

和 PCP、IPCP 一样，在 IOP 模型下构造的证明系统也可以类似转化成 IP 模型下的证明系统。

IPCP 模型可以看做特殊的 IOP 模型。在 IPCP 模型中，把对话环节的 Prover 消息都看做一个 PCP 预言机，那么一个 IPCP 模型下的协议就可以看做 IOP 模型下的协议。

IOP (Interactive Oracle Proofs)是一个交互式证明模型。
在一个交互式证明模型中，两个算法Prover和Verifier进行交互，Prover的目标是向Verifier证明一个实例x属于语言L。例如，对于RPT问题而言，实例x就是一个RS码f(S)，而语言L就是RS[F,S,ρ]。

IOP是在两个更早的交互式证明模型IP和PCP的基础上发展而来的。

IP (Interactive Proofs)：最早提出的交互式证明模型。在这个模型中，Prover和Verifier进行多轮交互，交互结束后，Verifier输出0或者1

PCP (Probabilistic Checkable Proofs)：在这个模型中，Prover和Verifier只进行一次交互，这一次交互中，Prover向Verifier发送一个字符串，叫做PCP。和IP的主要区别是，Verifier不需要读取完整的PCP字符串，而是可以对其进行随机访问。Verifier计算结束后，输出0或者1

IOP其实就是IP和PCP的结合：它像IP一样允许多轮交互，而每一轮交互都是一个PCP模型，即Verifier可以随机访问Prover发来的字符串，而不需要读取整个字符串。多轮交互结束后，Verifier输出0或者1。

IOP的一个变种叫做IOPP，这个多出来的P就是Proximity。在上一节介绍RPT时讲过，Proximity的意思是x要么是合法的，要么和L中的任何一个元素都相差至少δ距离。

PIOP

多项式 IOP (Polynomial IOP, PIOP) 模型是对 IOP 模型的进一步一般化。和 IOP 模型类似，在 PIOP 模型中，Verifier 向 Prover 发送消息，而 Prover 向 Verifier 发送预言机，不过这次不同的是，Prover 发送的是多项式预言机。

因为多项式预言机可以实现 PCP 预言机的功能，IOP 模型可以看做特殊的 PIOP 模型。

把 PIOP 模型下构造的证明系统转化为 IP 模型下的系统，基本思想是和 PCP、IPCP 以及 IOP 的情况一致的，即让 Prover 代替多项式预言机的角色，但是需要的密码学工具就不一样了。简单的 Merkle-Tree 或 VC 是不能模拟多项式预言机的。我们要用到一个更强大的密码工具，叫做多项式承诺 (Polynomial Commitment, PC)。

接下来我们介绍另外两个模型，LIP 和 LPCP。目前已有的 Verifier 复杂度和证明大小为常数级别的 zkSNARK 都是基于这两个模型构造的。

LIP

在线性 IP (Linear IP, LIP) 模型中，Prover 和 Verifier 进行对话。但是，相比于 IP 模型，增加了一些限制条件：Prover 只能是线性的。

这样一来，不仅 Prover，连 Verifier 也只能够进行线性运算了。这么一来，这个系统就没多大意义。为了能让 Verifier 做至少一次非线性运算，一个方法就是引入双线性对。双线性对允许对密文做乘法，但是乘法的计算结果是在另外一个密文空间中的，所以不影响安全性。

LPCP

参考：
[1]https://www.528btc.com/blocknews/160860602772697.html
[2]https://blog.nowcoder.net/n/f9742fdb7b2c459ca2be87c7ff5a7f46