专注网络与安全融合的全球网络安全领导者 Fortinet(NASDAQ:FTNT),近日宣布推出新一代自研安全芯片 FortiSP5,作为 Fortinet® ASIC 技术的最新突破,有力推动了分布式网络边缘安全的重大飞跃。FortiSP5 源自 Fortinet 二十余载对ASIC 创新投资和持续研发,与传统 CPU 和网络 ASIC 相比,具有非凡的安全计算能力及低成本、低功耗等优势,为企业分支机构、园区、5G网络、边缘计算、OT等防护领域构建全新安全基础设施。
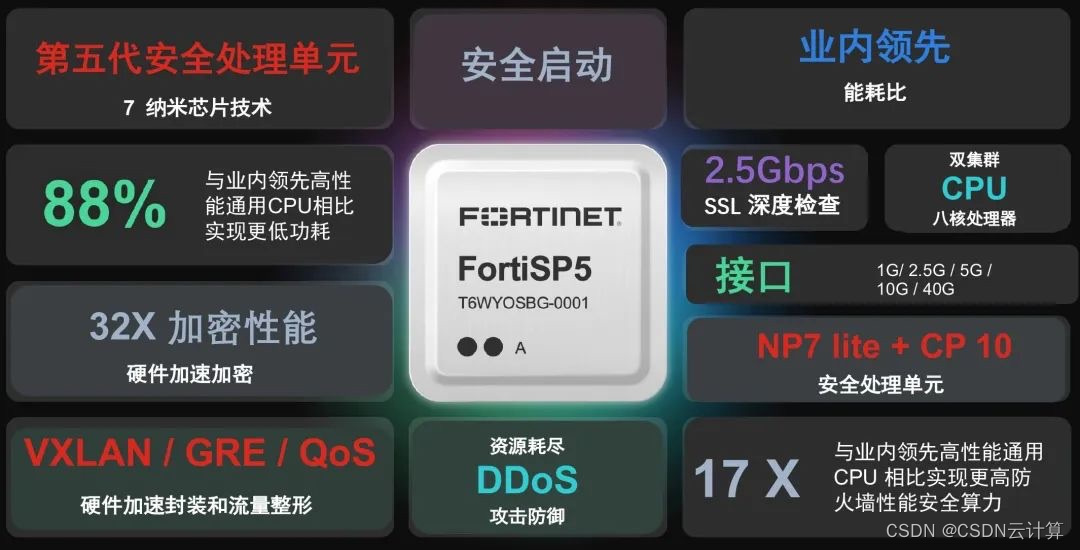
无与伦比的创新理念铸就新一代高性能定制芯片
FortiSP5 采用专用集成电路设计和嵌入式多核处理器,加速推进网络和安全功能深度融合,为用户提供:
• 防火墙性能大幅提升 17 倍,完胜业界通用CPU。
• 下一代防火墙(NGFW)性能提升 3.5 倍,遥遥领先业内高性能通用 CPU,快速处理的深度流量检查,全面检测和拦截各类威胁。
• 加解密速度提升 32 倍,实时保护敏感数据和虚拟专用网络。
• SSL 深度检测吞吐量高达 2.5 Gbps ,加速检查加密恶意流量的同时,确保卓越网络性能。
• 支持安全启动机制,仅允许授权操作系统软件启动,保护关键基础架构免受恶意篡改。
• 资源耗尽型DDoS攻击防护,有效拦截分布式拒绝服务(DDoS)攻击。
• VXLAN/GRE 硬件加速封装,快速实现分布式网络安全互连。
• 硬件加速型服务质量(QoS),满足视频会议等敏感应用 QoS 专项需求,优化用户体验。
显著节约成本和能耗
FortiSP5 第五代 7 纳米芯片,集成度更高,功能更强大:
• 与业内高性能通用 CPU 相比,功耗锐减 88%
• 行业领先功耗比优势
• 行业领先性价比优势
更多应用支持关键用例
与上一代产品相比,FortiSP5 的支持更多的应用场景以及更全面的加速能力,如下一代防火墙(NGFW)、零信任网络访问(ZTNA)、SD-WAN 和 SSL 检测,强劲支持以下用例:
• 分支机构/园区:FortiSP5 以更加的精简形态促进现有架构顺畅迁移至 SD-Branch,赋能IT 团队简化管理并降低运营成本,确保网络持续正常运行。此外,随着企业广泛采用云和混合办公模式,FortiSP5 将继续成为安全SD-WAN 的强劲驱动,助力用户随时随地安全无缝访问应用程序,尽享优化平台交付的一致用户体验。
• 边缘计算:边缘计算让数据处理更安全更高效并有效节约成本。在FortiSP5性能加持下,为商业和OT环境提供高速网络和安全威胁防护,轻松缓解流量移动瓶颈。
• OT场景:随着IT与OT的持续融合,基础设施运营中断的安全风险激增。搭载FortiSP5 的高性能单一平台,全方位守护 OT 和 IT 基础架构,快速实现可扩展的安全融合。
• 5G网络:随着企业5G网络技术的日益普及,用户坐享更高带宽和更低延迟的同时,持续推动边缘创新。FortiSP5 赋能进一步优化的可持续平台,支持企业网络无缝升级,畅游 5G高速网络。
久经验证的SoC技术
FortiSP5将为后续发布的下一代入门级和中端FortiGate防火墙提供强劲支撑。Fortinet 独家SoC技术现已推出第五代,性能久经验证,持续赋能业内性能卓越的产品和解决方案。示例包括:
• Fortinet 获评《2022 年 Gartner®网络防火墙魔力象限™报告》业内领导者殊荣1,这是 Fortinet 第十三次以领导者身份成功入围Gartner 网络防火墙魔力象限。
• Forrester 近期的一项研究2强调,部署由 FortiGate 和 SOC 技术提供强劲支撑的Fortinet 安全 SD-WAN 解决方案的用户,投资回收期仅为 8 个月,且在 3 年内实现 300% 的投资回报率。
Fortinet 始终贯彻可持续发展目标
FortiSP5 行业领先的能耗和性能优势以及搭载该加速芯片的产品,将助力企业大幅降低功耗并节省设备占地空间。Fortinet 始终以实际行动践行环保理念,致力于持续减少产品和解决方案资源消耗,并在日常业务运营中以创新为引领,以环境可持续为导向,进一步推动价值链的可持续发展。
如今,Fortinet Sunnyvale总部已成功实现净零排放,并计划到 2030 年实现全球运营完全碳中和目标。近期,Fortinet荣登 2022 年“道琼斯可持续发展全球指数”和“北美指数”榜单,成为全球顶级可持续发展的创新企业之一,彰显 Fortinet 致力于创建可持续发展社会的一贯承诺。
Fortinet 创始人、董事长兼首席执行官谢青表示:“随着 FortiSP5 的强势推出,Fortinet 再次缔造产品性能、成本和能耗全新行业记录。作为业内唯一一家搭载自研 ASIC加速芯片的网络安全厂商,Fortinet 自创立以来,坚持20 余载持续投入技术创新,为用户打造具有非凡安全计算能力的高性能芯片,高效赋能下一代安全基础设施。
行业权威证言
IDC企业网络研究经理Brandon Butler表示:“企业应用程序以及对其进行访问的用户和设备,部署空前分散,促使企业重新审视自身边缘网络和安全架构。构建企业边缘网络架构的关键在于,如何在不影响网络性能和用户体验的前提下,确保强效稳健的安全性。Fortinet 深耕 ASIC 技术创新 20 余载,专注企业迫切需求和目标,其新一代 FortiSP5 加速芯片充分沿袭了这一理念。Fortinet 网络与安全融合解决方案组合在定制加速芯片的强力驱动下,助力企业加速边缘网络构建和安全转型。”
引用来源:
1. Gartner, Magic Quadrant for Network Firewalls, Rajpreet Kaur, Adam Hils, Tom Lintemuth, 19 December 2022.
2. The Total Economic Impact™ Of Fortinet Secure SD-WAN”, a commissioned study conducted by Forrester Consulting on behalf of Fortinet, December 2022.