上篇文章讲述了“单因素方差分析全流程总结”，单因素方差分析只是考虑了一个自变量（定类）与一个因变量（定量）之间的关系，但是在实际问题研究中可能研究两个或者几个因素与因变量之间的关系，例如，分析产品满意度与学历、品牌满意度等的关系。当方差分析中研究几个自变量和1个因变量之间的关系时，称为多因素方差分析。如果是两个自变量则为双因素方差分析。

一、案例与数据

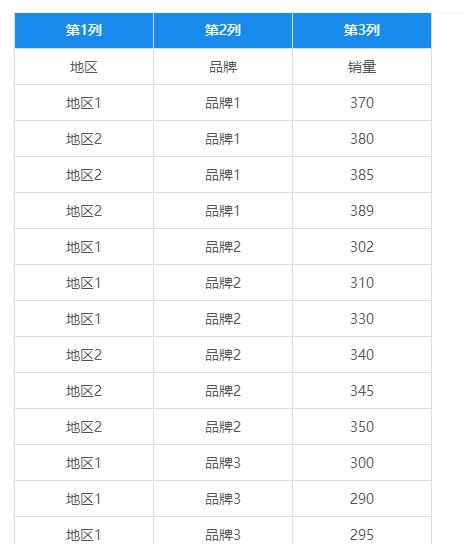
有四个品牌的吸尘器在两个地区的不同门店销售，为分析吸尘器的品牌和销售地区对销售量的影响，搜集每个品牌在各地区的销售数据，销售经理根据搜集的数据想要进行分析品牌和地区对吸尘器的销售量是否有显著差异以及两个因素搭配是否对销售量产生新的影响，部分数据如下：

二、分析问题

例子中涉及三个变量，一个是“地区”一个是“品牌”还有一个是“销售量”。其中“地区”和“品牌”是定类变量，“销售量”是定量变量，想要进行分析品牌和地区对吸尘器的销售量是否有显著差异，分析究竟是一个因素在起作用，还是两个因素都在起作用，还是两个因素都不起作用。这就是一个双因素方差分析问题。

三、分析前准备

在进行双因素方差分析前需要进行分析前准备，首先进行数据的异常值检查，然后验证数据是否满足双因素方差分析的要求：

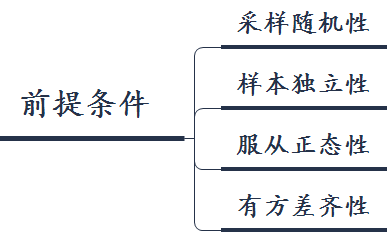
案例已经满足前两个条件，只需验证在个总体中，每个总体服从正态分布和方差齐性。

1、异常值检验

异常值是指在数据中不正常的值，也称离群值，比如大于三倍标准差等。与其它方差分析一致，双因素方差分析对异常值也比较敏感，这些数据可能会导致分析结果异常，比如扭曲各分类之间的差异，所以检验异常值尤为重要。利用SPSSAU箱线图进行查看直观且容易查看异常值点。

不同地区的销量：

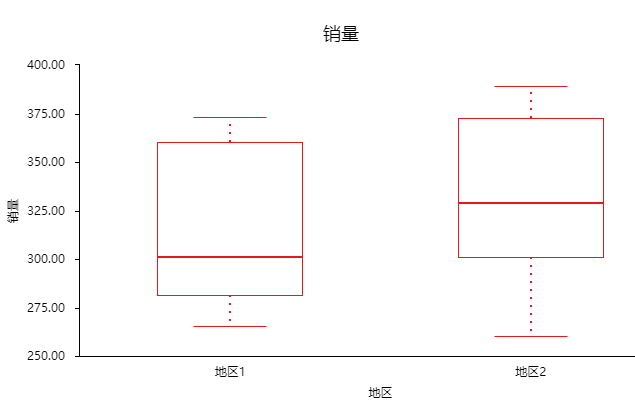
从箱线图中可以看出不同地区吸尘器的销量没有发现异常值。

不同品牌的销量：

从箱线图中可以看出不同品牌吸尘器的销量没有发现异常值。综上：数据中暂未发现异常值，不需要处理。

那么如果出现异常值如何处理呢？

常见做法是将异常值剔除，重新进行分析，有时异常值数量较多，不希望剔除，那么也可以处理为缺失值进行填补（一般平均值和中位数等使用较多），或者利用插值法进行插值。接下来进行检查数据是否符合方差分析的前提条件，首先进行正态性检验。

2、正态性检验

检验数据是否服从正态分布有很多种方式其中包括正态性检验以及图示化P-P图或者Q-Q图等，例子中要检验每个总体是否服从正态分布，由于正态性检验最为严谨，所以这里使用正态性检验进行分析。不同品牌的销量结果如下：

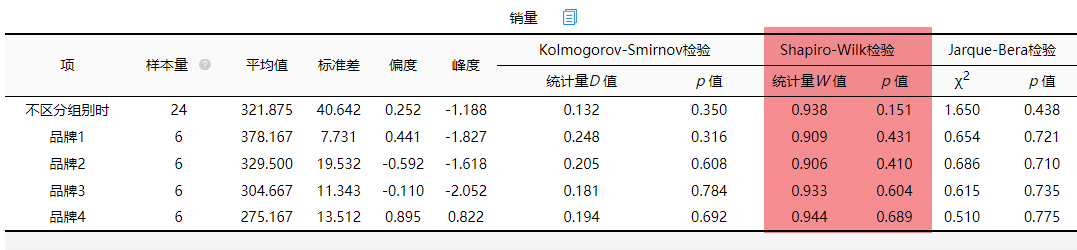
SPSSAU共提供三种正态性检验其中包括K-S检验（Kolmogorov-Smirnov检验）、S-W检验（Shapiro-Wilk检验）以及J-B检验（Jarque-Bera检验），由于每个个体的样本为6个总样本量为24个小于50所以为小样本分析，使用S-W检验进行分析即可，如果样本量较大（比如大于50）可以考虑使用K-S或者J-B检验。发现S-W检验中p值均大于0.05，所以不同地区的销量满足正态性检验，不同地区吸尘器的销量分析也是如此：

综上，每个总体服从正态分布，接下来验证是否服从方差齐性。

3、方差齐检验

方差齐性指自变量X的取值范围内，不论X取什么值，对应的Y为服从正态分布的随机变量，并具有相同的方差，即Y的方差与X值的大小无关（来源百度百科）。利用SPSSAU进行方差齐检验（分析路径【通用方法】→【方差】）。不同地区的销量方差齐分析如下：

利用方差齐性检验各组别数据的波动情况，从方差齐分析结果中可以看出结果的F值为0.043，p值为0.838大于0.05，说明不同地区的销量没有显著差异性，也即说明具有方差齐性，同理可以分析不同品牌的销量也具有方差齐性（不进行赘述）。

综上，每个总体服从方差齐性，并且满足双因素方差分析的前提条件，所以接下来进行双因素方差分析。

四、双因素方差分析

为了研究品牌和地区对吸尘器的销售量是否有显著差异以及两个因素搭配是否对销售量产生新的影响，以品牌和地区作为自变量，以销售量作为因变量进行双因素方差分析。

1、主效应

考虑某因素的主效应时，需要考虑除所有因素的效应，简单来说就是X对Y的影响。比如：双因素方差分析中，分别去判断“地区”和“品牌”对销售量的影响。

结果如下：

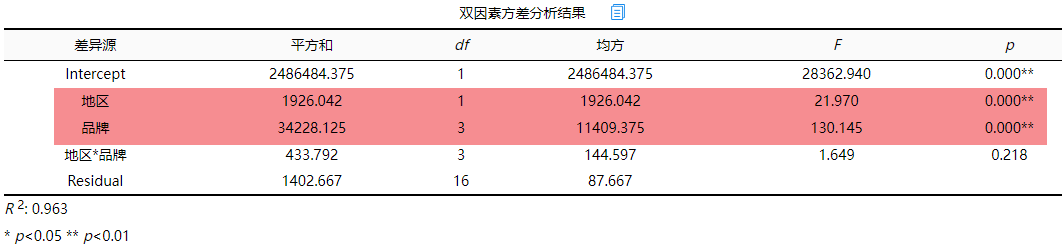
首先进行查看变量“地区”，发现自变量地区的F值为21.970，并且p值小于0.05所以说明主效应存在，然后对“品牌”进行分析，发现品牌的F值为130.145并且p值小于0.05所以说明主效应存在，具体差异可以进行事后多重比较进行分析。接下来研究“地区”和“品牌”搭配是否对销售量产生新的影响，进行查看交互效应。

2、交互效应

在双因素方差分析中，如果除了研究品牌和地区对销售量的影响还研究两个因素搭配是否对销售量产生新的影响，例如例子中的某个地区对某种品牌吸尘器有特殊偏好，则为双因素方差分析的交互作用分析，即交互效应。

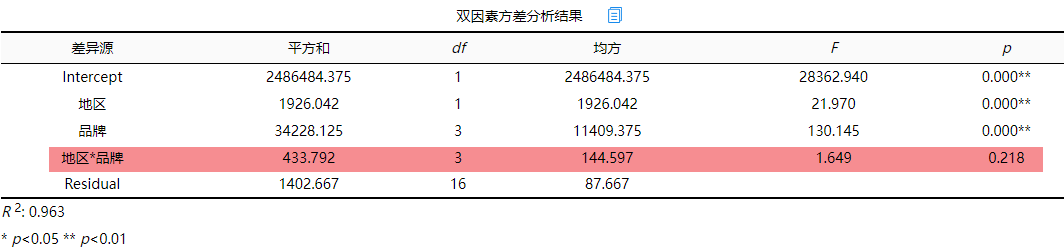
从上表可以看出，分析项为“地区与品牌的交互项”因变量为“销售量”发现模型的F值为1.649,并且p值为0.218大于0.05，所以模型不显著，即说明没有交互效应。分析完毕。综上，存在主效应但不存在交互效应，接下来进一步分析。

五、进一步分析

如果进行双因素方差分析，一般是主效应显著后才会进一步查看事后多重比较，对于交互作用显著的模型才会更深一步研究简单效应分析。

1、简单效应

简单效应是指简单效应指X1在某个水平时，X2不同水平的比较；因为该模型只存在主效应所以进行事后多重比较不进行简单效应分析。如果存在交互效应，则可以进一步分析简单效应。

2、事后多重比较

因为主效应显著，并且“地区”和“品牌”两个主效应都显著，所以进行事后多重比较，进一步分析（此处利用LSD方法进行，因为该方法对差异最为敏感使用最为广泛，并且检验效能高，对比组别较少时使用，除此之外SPSSAU还提供其它方法，比如：Bonferroni校正等）。

“地区”事后多重比较：

比较不同地区的销量是否有显著性差异，上表可以看出t值为-4.687，p值远小于0.05所以地区1和地区2的销量有显著性差异并且地区1与地区2的均值差值为负数，说明地区2的均值更大，从侧面说明地区2的销量更好。

“品牌”事后多重比较：

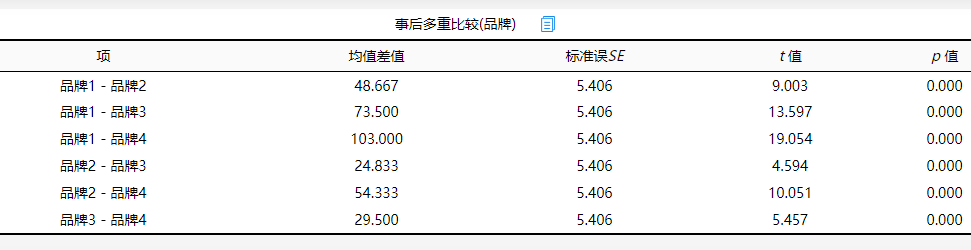
比较不同品牌的销量是否有显著性差异，上表可以看出品牌1、品牌2、品牌3、品牌4两两之间比较，p值均远小于0.05所以不同品牌两两之间的销量均有显著性差异，并且从均值差值中可以看出品牌1的均值更大，从侧面说明品牌1的销量更好。

六、总结

通过双因素方差分析研究了“品牌和地区对吸尘器的销售量是否有显著差异以及两个因素搭配是否对销售量产生新的影响”，最后发现品牌和地区对吸尘器的销售量有显著性差异，但是两个因素搭配并未对对销售量产生新的影响，并且利用事后多重比较进一步分析发现不同地区对销售量有显著性差异，并且地区2销量更好，不同品牌两两之间的销量均有显著性差异品牌1的销量更好，所以公司在做决策时可以重点分析地区2和品牌1的特点或者策略等。