题目链接

Leetcode.1401 圆和矩形是否有重叠 Rating ： 1709

题目描述

给你一个以 (radius, xCenter, yCenter)表示的圆和一个与坐标轴平行的矩形 (x1, y1, x2, y2)，其中 (x1, y1)是矩形左下角的坐标，而 (x2, y2)是右上角的坐标。

如果圆和矩形有重叠的部分，请你返回 true，否则返回 false。

换句话说，请你检测是否 存在 点 (xi, yi)，它既在圆上也在矩形上（两者都包括点落在边界上的情况）。

示例 1 ：

输入：radius = 1, xCenter = 0, yCenter = 0, x1 = 1, y1 = -1, x2 = 3, y2 = 1
输出：true
解释：圆和矩形存在公共点 (1,0) 。

示例 2 ：

输入：radius = 1, xCenter = 1, yCenter = 1, x1 = 1, y1 = -3, x2 = 2, y2 = -1
输出：false

示例 3 ：

输入：radius = 1, xCenter = 0, yCenter = 0, x1 = -1, y1 = 0, x2 = 0, y2 = 1
输出：true

提示：

• $1<=radius<=2000$
• $-10^4<=xCenter,yCenter<=10^4$
• $-10^4<=x1<x2<=10^4$
• $-10^4<=y1<y2<=10^4$

分析：

(x0,y0)是矩形的中心点，将其作为坐标系的原点，便于处理。

c是矩形的中心 (x0,y0)到圆心(xCenter,yCenter)的向量。

a是矩形的中心 (x0,y0)到(x2,y2)的向量。

b就是我们要求的 矩形 到 圆的向量，b = { c[0] - a[0] , c[1] - a[1] }。

我们只需要判断 向量b的模长 是否小于等于 圆的半径radius即可（判断 矩形 是否和 圆 相交）。

还有一些特殊情况：

此时 c[0] - a[0] < 0，所以我们就可以把它看成 0，即b = { 0 , c[1] - a[1] }，就变成我们实际上要求的向量 u。

此时 c[1] - a[1] < 0，所以我们就可以把它看成 0，即b = { c[0] - a[0] ，0 }，就变成我们实际上要求的向量 u。

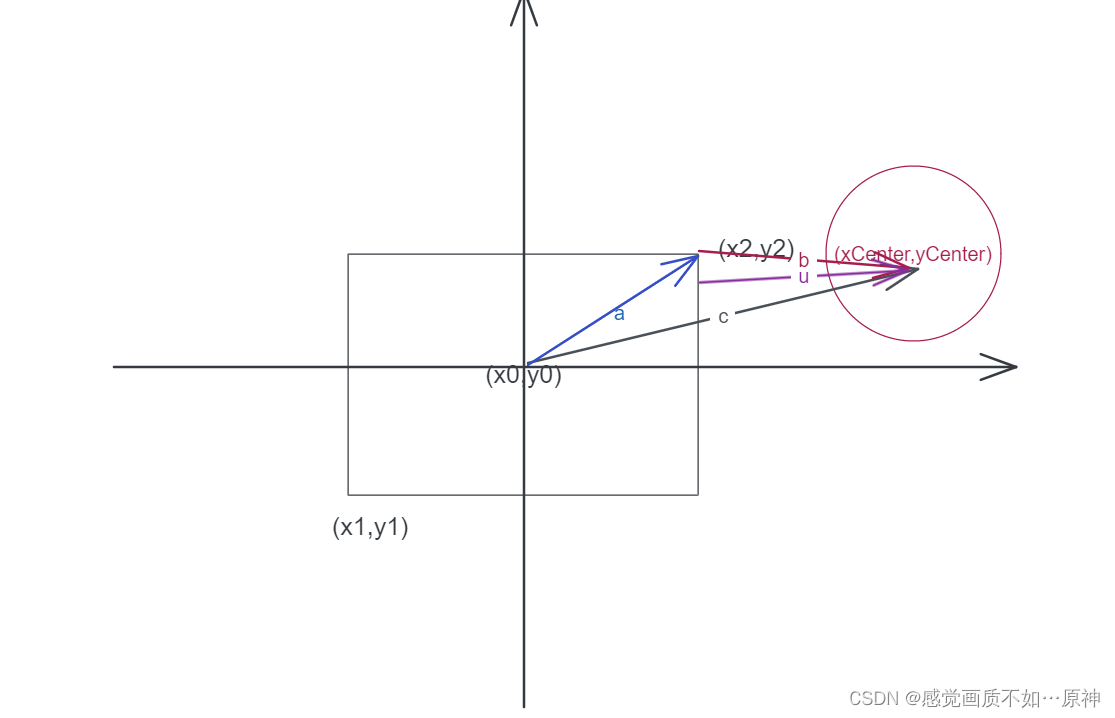
判断圆和矩形是否相交参考这个

时间复杂度 : $O(1)$

C++代码：

class Solution {
public:
    bool checkOverlap(int radius, int xCenter, int yCenter, int x1, int y1, int x2, int y2) {
        //求矩形中心点
        double x0 = (x1+x2)/2.0;
        double y0 = (y1+y2)/2.0;

        //求向量 c ， a
        //用绝对值是为了让 x分量 和 y分量 都为正数，相当于将其映射到了第一象限（因为第一象限的坐标值都是正数）
        vector<double> c {abs(xCenter - x0),abs(yCenter - y0)};
        vector<double> a {x2 - x0,y2 - y0};

        //求向量 b 如果其中一个分量是负数的话，直接看作0
        vector<double> b {max(c[0] - a[0],0.0),max(c[1] - a[1],0.0)};

        
        return b[0] * b[0] + b[1] * b[1] <= radius * radius;
    }
};

Java代码：

class Solution {
    public boolean checkOverlap(int radius, int xCenter, int yCenter, int x1, int y1, int x2, int y2) {
        double x0 = (x1+x2)/2.0;
        double y0 = (y1+y2)/2.0;

        double[] c = new double[2];
        double[] a = new double[2];
        double[] b = new double[2];

        c[0] = Math.abs(xCenter - x0);
        c[1] = Math.abs(yCenter - y0);

        a[0] = x2 - x0;
        a[1] = y2 - y0;

        b[0] = Math.max(c[0] - a[0],0.0);
        b[1] = Math.max(c[1] - a[1],0.0);

        return b[0]*b[0] + b[1]*b[1] <= radius*radius;
    }
}