1. 题目介绍（）

写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项（即 F(N)）。斐波那契数列的定义如下：

F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.

斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。
答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

【测试用例】：
示例 1：

输入：n = 2
输出：1

示例 2：

输入：n = 5
输出：5

【条件约束】：

提示：

0 <= n <= 100

2. 题解

2.1 递归实现 — O(2ⁿ)

时间复杂度O(2ⁿ)，空间复杂度O(1)

class Solution {
    // 第一种方法：递归实现
    public int fib(int n) {
        // 1. n为0时，返回0
        if (n == 0) return 0;
        // 2. n为1时，返回1
        else if (n == 1) return 1;
        // 3. 从第三个数开始，之后的每个数都为前两项数的和
        else return fib(n-1) + fib(n-2);
    }
}

在这里插入图片描述
改进： 使用数组保存每一次的运算结果；改进之后时间复杂度：从2的n次方降为了O(n²)，空间复杂度：O(n)。

class Solution {
    int[] ints;
    
    public int fib(int n) {
        ints = new int[n];
        if(n <= 1) return n;
        return (f(n - 1) + f(n - 2)) % 1000000007;
    }
    private int f(int n) {
        if(n == 0 || n == 1) return n;
        if (ints[n] != 0){
            return ints[n];
        }
        ints[n] = (f(n - 1) + f(n - 2)) % 1000000007;
        return (f(n - 1) + f(n - 2)) % 1000000007;
    }
}

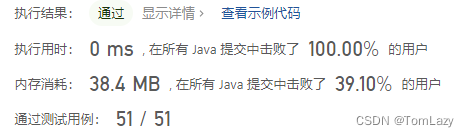
在这里插入图片描述

2.2 滚动数组循环实现

时间复杂度O(n)，空间复杂度O(1)
在这里插入图片描述
数组不断滚动向后，逐次累加

class Solution {
    // 第二种方法：循环实现
    public int fib(int n) {
        final int MOD = 1000000007;
        // 1. 定义辅助数组res，用以记录当前值的前两项值
        long[] res = {0,1};
        // 2. 如果n小于2，直接返回
        if (n < 2){
            return (int)res[n];
        } 
        // 3. 定义sum，用于记录从第三项开始，所得到的前两项加和
        long sum  = 0;
        for (int i = 2; i <= n; i++){    
            // 4. sum为前两项加和，然后依次交换元素，逐次相加
            sum = (res[0] + res[1]) % MOD;
            res[0] = res[1];
            res[1] = sum;
        }
        return (int)sum;
    }
}

在这里插入图片描述

2.3 矩阵快速幂 – O(logn)

时间复杂度O(logn)，空间复杂度O(1)
在这里插入图片描述
这就涉及到了斐波那契数列的数学公式。

快速幂算法原理: 如需求数据 a 的幂次，此处 a 可以为数也可以为矩阵，常规做法需要对a进行不断的乘积即 a * a * a * …

以求 3^10 的结果为例：
[优化步骤1：]
易知：
3^10=3*3*3*3*3*3*3*3*3*3
=9^5 = 9^4*9
=81^2*9
=6561*9

基于以上原理，我们在计算一个数的多次幂时，可以先判断其幂次的奇偶性，然后：

如果幂次为偶直接 base(底数) 作平方，power(幂次) 除以2
如果幂次为奇则底数平方，幂次整除于2然后再多乘一次底数

[优化步骤2：]

对于以上涉及到 [判断奇偶性] 和 [除以2] 这样的操作。使用系统的位运算比普通运算的效率是高的，因此可以进一步优化：

把 power % 2 == 1 变为 (power & 1) == 1
把 power = power / 2 变为 power = power >> 1

class Solution {
    static final int MOD = 1000000007;
    public int fib(int n) {
        //矩阵快速幂
        if (n < 2) {
            return n;
        }
        //定义乘积底数
        int[][] base = {{1, 1}, {1, 0}};
        //定义幂次
        int power = n - 1;
        int[][] ans = calc(base, power);
        //按照公式，返回的是两行一列矩阵的第一个数
        return ans[0][0];
    }

    //定义函数,求底数为 base 幂次为 power 的结果
    public int[][] calc(int[][] base, int power) {
        //定义变量，存储计算结果，此次定义为单位阵
        int[][] res = {{1, 0}, {0, 1}};

        //可以一直对幂次进行整除
        while (power > 0) {
            //1.若为奇数，需多乘一次 base
            //2.若power除到1，乘积后得到res
            //此处使用位运算在于效率高
            if ((power & 1) == 1) {
                res = mul(res, base);
            }
            //不管幂次是奇还是偶，整除的结果是一样的如 5/2 和 4/2
            //此处使用位运算在于效率高
            power = power >> 1;
            base = mul(base, base);
        }
        return res;
    }

    //定义函数,求二维矩阵：两矩阵 a, b 的乘积
    public int[][] mul(int[][] a, int[][] b) {
        int[][] c = new int[2][2];
        for (int i = 0; i < 2; i++) {
            for (int j = 0; j < 2; j++) {
                //矩阵乘积对应关系，自己举例演算一遍便可找到规律
                c[i][j] = (int) (((long) a[i][0] * b[0][j] + (long) a[i][1] * b[1][j]) % MOD);
            }
        }
        return c;
    }
}