题目链接

Leetcode.2257 统计网格图中没有被保卫的格子数 Rating ： 1709

题目描述

给你两个整数 m和 n表示一个下标从 0开始的 m x n网格图。同时给你两个二维整数数组 guards和 walls，其中 guards[i] = [rowi, coli]且 walls[j] = [rowj, colj]，分别表示第 i个警卫和第 j座墙所在的位置。

一个警卫能看到 4个坐标轴方向（即东、南、西、北）的 所有 格子，除非他们被一座墙或者另外一个警卫 挡住 了视线。如果一个格子能被 至少 一个警卫看到，那么我们说这个格子被 保卫 了。

请你返回空格子中，有多少个格子是 没被保卫 的。

示例 1：

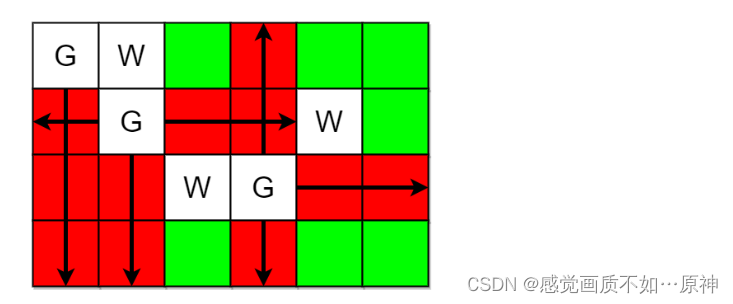
输入：m = 4, n = 6, guards = [[0,0],[1,1],[2,3]], walls = [[0,1],[2,2],[1,4]]
输出：7
解释：上图中，被保卫和没有被保卫的格子分别用红色和绿色表示。
总共有 7 个没有被保卫的格子，所以我们返回 7 。

示例 2：

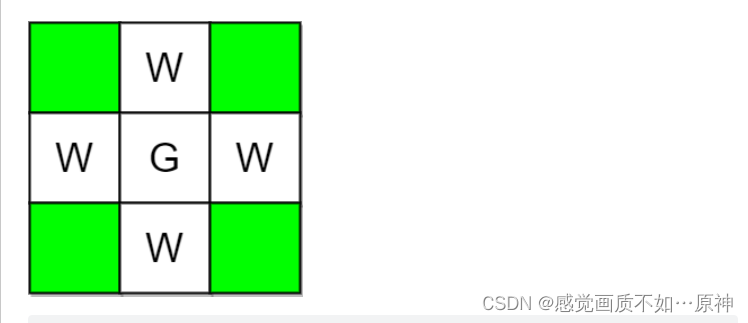
输入：m = 3, n = 3, guards = [[1,1]], walls = [[0,1],[1,0],[2,1],[1,2]]
输出：4
解释：上图中，没有被保卫的格子用绿色表示。
总共有 4 个没有被保卫的格子，所以我们返回 4 。

提示：

• $1<=m,n<=10^5$
• $2<=m\ast n<=10^5$
• $1<=guards.length,walls.length<=5\ast 10^4$
• $2<=guards.length+walls.length<=m\ast n$
• $guards[i].length==walls[j].length==2$
• $0<=rowi,rowj<m$
• $0<=coli,colj<n$
• guards和 walls中所有位置 互不相同 。

分析：

我们先建立一个 m*n的表格g。

g[i][j] = -1代表位置 (i,j)有 墙。

g[i][j] = 2代表位置 (i,j)有 警卫。

g[i][j] = 1代表位置 (i,j)已经被 警卫 看过了。

我们从每个 警卫的位置开始 BFS（上下左右四个方向遍历），遇到墙 或者 遇到警卫（如果遇到另一个警卫，当前警卫就不看了，让这个新遇到的警卫再看下去） 该方向就停止遍历。

时间复杂度：$O(m\ast n)$

C++代码：

int dx[4] = {1,0,-1,0};
int dy[4] = {0,1,0,-1};
class Solution {
public:
    int countUnguarded(int m, int n, vector<vector<int>>& guards, vector<vector<int>>& walls) {
        //建表
        vector<vector<int>> g(m,vector<int>(n));

        for(auto &e:walls) g[e[0]][e[1]] = -1;
        for(auto &e:guards) g[e[0]][e[1]] = 2;

        for(auto &e:guards){
            int x = e[0],y = e[1];
            //从上下左右 四个方向遍历
            for(int i = 0;i < 4;i++){
                int nx = x + dx[i],ny = y + dy[i];
                //如果越界 或者 当前位置是墙 或者 当前位置是警卫 都停止遍历
                while(nx >= 0 && nx < m && ny >= 0 && ny < n && g[nx][ny] != 2 && g[nx][ny] != -1){
                    g[nx][ny] = 1;
                    nx += dx[i];
                    ny += dy[i];
                }
            }
        }

        int ans = 0;
        //最后统计没有被警卫守卫的点 即 g[i][j] == 0 的点
        for(int i = 0;i < m;i++){
            for(int j = 0;j < n;j++){
                if(g[i][j] == 0) ans++;
            } 
        }
        return ans;
    }
};

Java代码：

class Solution {
    int[] dx = {1,0,-1,0};
    int[] dy = {0,1,0,-1};
    public int countUnguarded(int m, int n, int[][] guards, int[][] walls) {
        int[][] g = new int[m][n];
        for(var e:walls) g[e[0]][e[1]] = -1;
        for(var e:guards) g[e[0]][e[1]] = 2;

        for(var e:guards){
            int x = e[0];
            int y = e[1];
            for(int i = 0;i < 4;i++){
                int nx = x + dx[i];
                int ny = y + dy[i];
                while(nx>=0 && nx<m && ny>=0 && ny<n && g[nx][ny]!=2 && g[nx][ny]!=-1){
                    g[nx][ny] = 1;
                    nx += dx[i];
                    ny += dy[i];
                } 
            }
        }

        int ans = 0;
        for(int i = 0;i < m;i++){
            for(int j = 0;j < n;j++){
                if(g[i][j] == 0) ans++;
            }
        }
        return ans;
    }
}