一.反向传播

        本章将介绍能够高效计算权重参数的梯度的方法——误差反向传播法，这里简单介绍一下什么是反向传播，加入有个函数y = f(x)，那么它的反向传播为图下这个样子：

        反向传播的计算顺序是，将输入信号E乘以节点的局部导数，然后将结果传递给下一个节点。这里所说的局部导数是指正向传播中y = f(x) 的导数，也就是y 关于x的导数。比如，假设y = f(x) = x^2，则局部导数为= 2x。把这个局部导数乘以上游传过来的值（本例中为E），然后传递给前面的节点。

二.加法的反向传播

        这里以z = x + y 为对象来观察它的反向传播，z = x + y的导数可由下式计算出来：

        使用计算图表示则如下图：

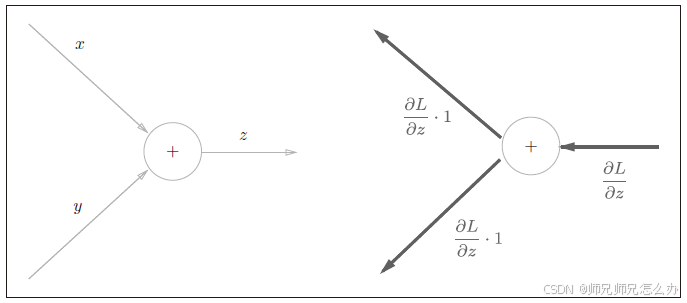
        可以观察到，反向传播将从上游传过来的导数乘以1，然后传向下游。也就是说，加法节点的反向传播只乘以1，所以输入的值会原封不动地流向下一个节点。

三.乘法的反向传播

        接下来，我们看一下乘法节点的反向传播。这里我们考虑z = xy。这个式子的导数用图下表示。

        乘法的反向传播会将上游的值乘以正向传播时的输入信号的“翻转值”后传递给下游。如下图所示：

        正向传播时信号是x的话，反向传播时则是y；正向传播时信号是y 的话࿰