目录
前言
1. 被控对象(被观测对象)
2.非线性观测器
2.1仿真分析
2.2仿真模型
2.3仿真结果
3.线性观测器
3.1仿真模型
3.2仿真结果
4.总结和学习问题
前言
什么叫观测器?为什么该类观测称为扩张观测器?
:观测器可以理解为所观测对象的“克隆”,即形式与被观测对象相像,理论上通过调参可以复刻的一模一样;之所以叫“扩张”是因为相较于所观测对象,观测器多了一个状态,这个状态可以是扰动项。所以观测器有时候可以称为扰动观测器。
前面基于滑模理论的知识,也介绍了,个人认为都差不多,只不过反馈的函数多种多样:
基于扩张观测器(LESO)的滑模控制_Mr. 邹的博客-CSDN博客
1. 被控对象(被观测对象)
这里以二阶系统为例,并且引入未知项f(x1,x2):
2.非线性观测器
三阶非线性观测器:

饱和函数(作用:抑制信号抖振):
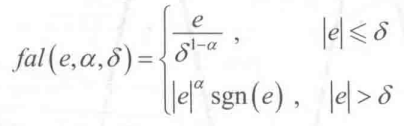
其中:
![]()
2.1仿真分析
这里假设ut=sin(t),取观测器调节参数:β1=100,β2=300,β3=1000.
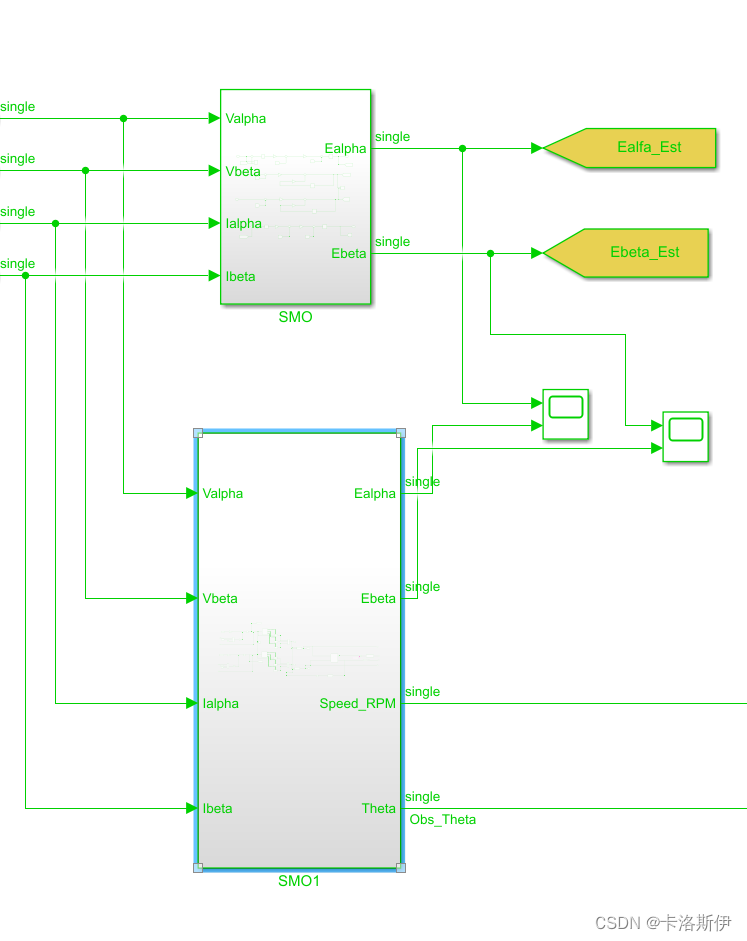
2.2仿真模型

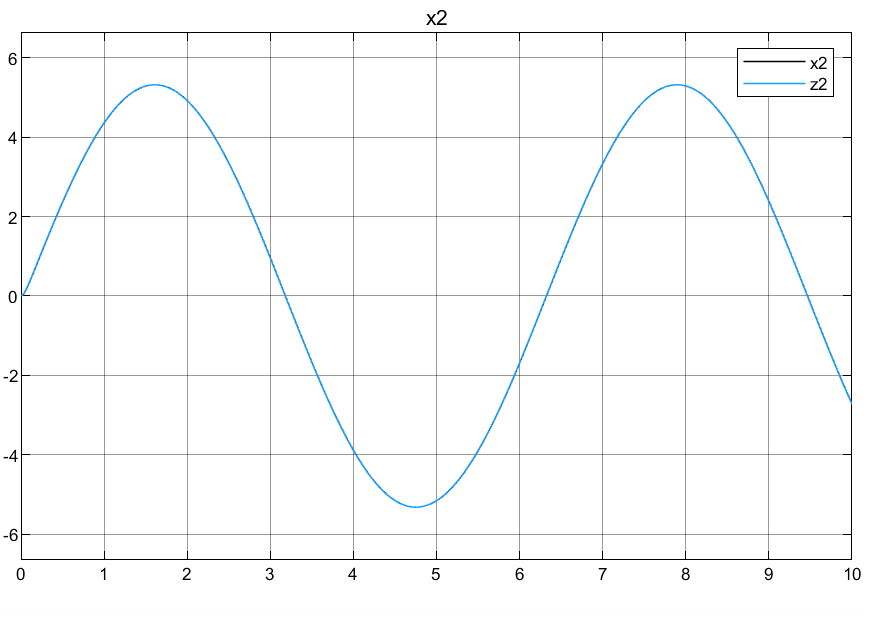
2.3仿真结果

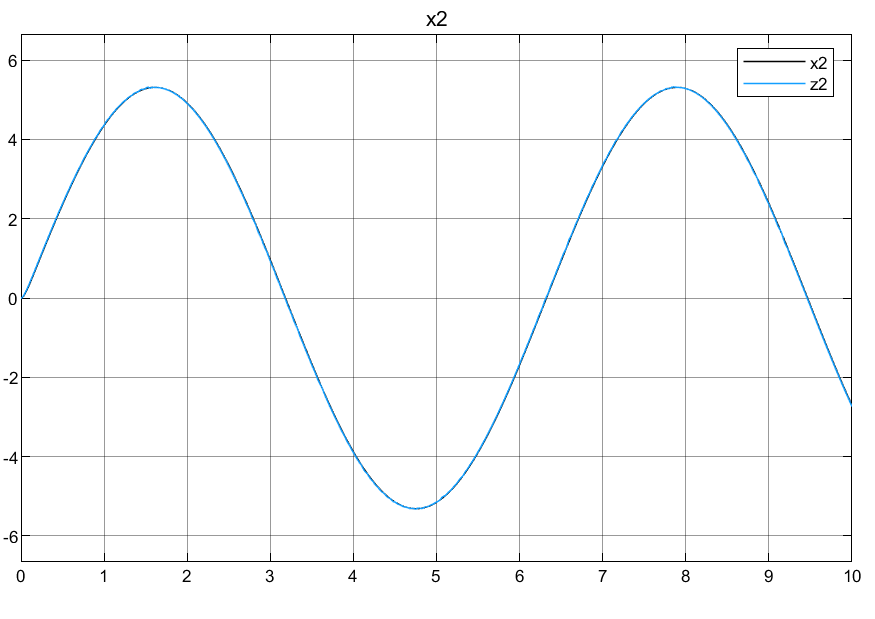
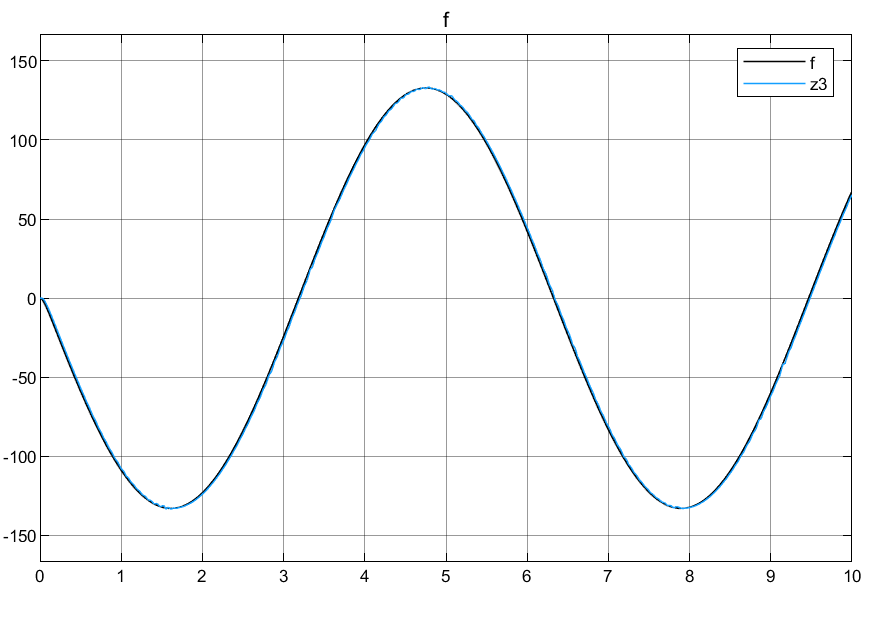
3.线性观测器
对于线性观测器,就是上篇文章:基于扩张观测器(LESO)的滑模控制_Mr. 邹的博客-CSDN博客
这里为了对比一下两种仿真的效果,将LESO也放在本篇文章的系统中:
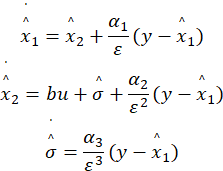
其中,ε > 0,且α1、α2、α3均为正实数,即满足如下多项式为Hurwitz多项式:
![]()
3.1仿真模型

3.2仿真结果

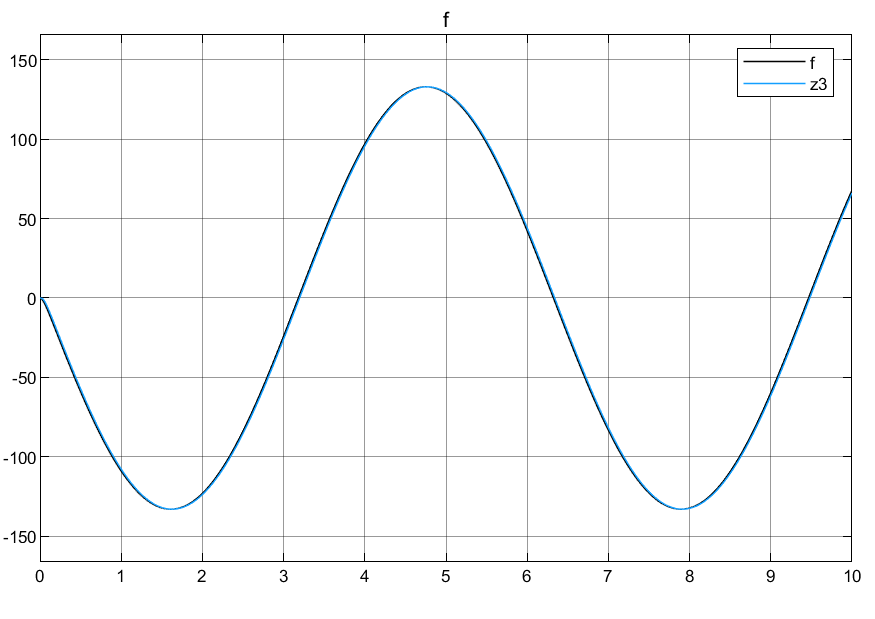
4.总结和学习问题
①可以理解我之前基于观测器滑模控制文章中的观测器为LESO,本篇的是NLESO.
②观测器调参经验:
(1)宽带调参:β1=3*w0,β2=3*w0^2,β3=w0^3时,w0 = 50调节LESO效果很好。
(2)保证特征方程为Hurwitz多项式调参(此处为3阶观测器):(s+λ)^3=s^3+3(s^2)λ+3s(λ^2)+λ^3,而ε的调节一般为仿真步长0.01,所以只需要调节λ即可,可以理解为"高增益"调参,最后得到α1=3λ、α2=3(λ^2)、α2=λ^3,这里选取λ=2,LESO效果良好。
③对于NLESO宽带调参β1=3*w0,β2=3*w0^2,β3=w0^3时(无论w0如何调节),参数调节的效果劣于100、300、1000这组参数,这是缘何?因为宽带调参是高志强老师对于LESO上提出的,那NLESO上调参有何方法么?
④LESO效果可以做到和NLESO一样,为什么还要NLESO?从鲁棒性角度考虑?但是LESO实践证明也有很强鲁棒性呀!
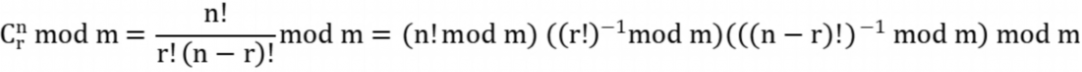





![[LeetCode周赛复盘] 第 333 场周赛20230219](https://img-blog.csdnimg.cn/29f6f204ccfb4ecf90a7b04f6c94d905.png)