论文信息

name_en: Mastering the game of Go without human knowledge
name_ch: 在没有人类知识的情况下掌握围棋游戏
paper_addr: http://www.nature.com/articles/nature24270
doi: 10.1038/nature24270
date_publish: 2017-10-01
tags: [‘深度学习’,‘强化学习’]
if: 69.504 Q1 B1 Top
journal: Nature
author: David Silver
zotero id: 8Z2VCLXT
citation: 8443

读后感

AlphaGo Zero是AlphaGo的改进版本，之前版本都使用有监督学习和强化学习相结合的方式。如题——它与之前版本不同的是不需要通过学习人类棋手的下法，其Zero 意思是无师自通。其核心算法是将价值网络和策略网络二合一，并在卷积网络中加入残差。

介绍

文章分两部分，第一部分介绍其整体，第二部分展示了算法细节和一些背景知识（在参考资料之后）。
AlphaGo 是深度强化学习的精典应用范例，围棋领域之所以复杂是因为：在广阔的搜索空间中，需要有精确而精细的前瞻性。

AlphaGo的第一个版本，简称AlphaGo Fun，指2015年战胜樊麾的版本；它使用两个神经网络：价值网络和策略网络。其中的策略网络一开始通过专家数据有监督训练，后期利用强化学习细化；价值网络通过策略网络自我对弈得到数据，从中采样训练；通过蒙特卡洛树搜索(MCTS)，价值网络用于计算树中节点的价值，策略网络用于计算最高价值的策略。Alpha Lee是第二个版本，在2016年战胜了李世石，它相对第一版进行了微调，且具有更大的神经网络，也需要更大算力。Alpha Master 是进一步优化版本。

相对于之前版本，AlphaGo Zero有以下优势：

• 使用自我对弈的强化学习，不需要专家知识
• 只使用了棋盘上的黑白子作为输入特征，没有手工构造特征
• 使用单网络：结合了价值网络和策略网络
• 使用简单的树搜索，而不依赖蒙特卡洛展开（Monte Carlo rollouts）

AlphaGo Zero中的强化学习

设环境状态为s，它包含当前状态和历史数据；p表示策略概率，v是当前状态s最终获胜的概率：
$$(p,v)=f_{\theta }(s)$$
其中f是神经网络，theta是网络参数，它根据当前状态输出策略和价值。Zero还对神经网络结构进行了调整：对卷积层加入了残差块，以实现批量归一化和非线性整流。

在每个状态s，都执行神经网络引导下的MCTS搜索，输出是每一种走法的概率π，它先于直接使用f网络输出的策略p，也就是说MCTS改进了神经网络输出的策略。自我对弈后是否胜利又可作为更强的策略评估。训练的目标包含两个：能更准确地评估p和v，且能最终取胜。

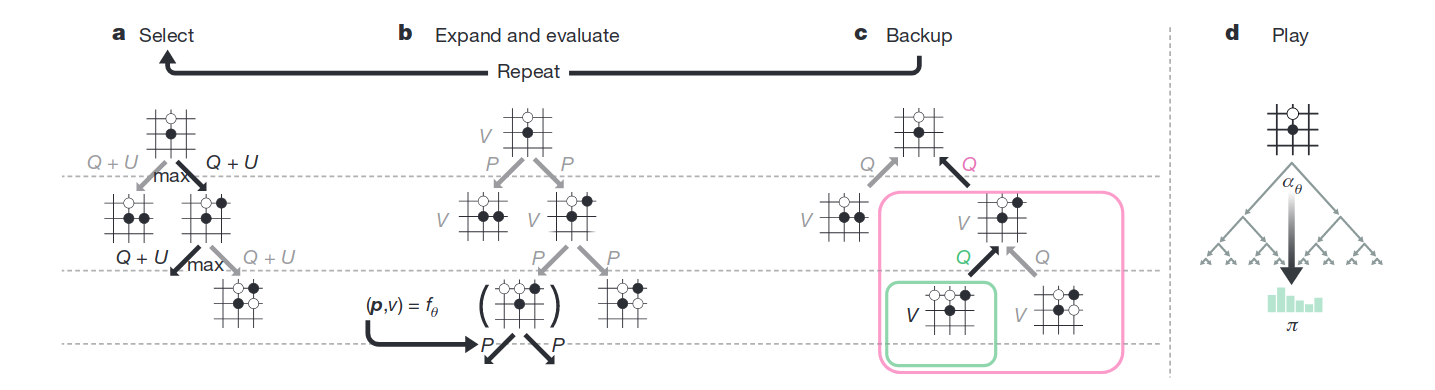
图-2展示了每一次模拟的过程：

• 树中的每个边是其上状态s和选择动作a的组合；
• 每条边都包含：动作的先验概率P(s,a)，该边的访问次数N(s,a)，动作价值Q(s,a）
• 每一步都选择Q+U最大(上图中子图1)，以确认下一步走法，其中U是上置信区间：
  $$U(s,a)\propto P(s,a)/(1+N(s,a))$$
  这里的P可视为神经网络f的策略输出（上图中子图2），而引入N是为了平衡探索与利用。当N值小访问次数少时，U更大，以鼓励探索未知领域。
  Q计算了下一步可能动作a能到达的状态s’的平均价值（上图中子图3）：
  $$Q(s,a)=1/N(s,a)\sum _{s^{\prime }\mid s,a\to s^{\prime }}V\left(s^{\prime }\right)$$
• 当搜索完成后，返回搜索概率π

最终公式如下：
$$(\mathbf{p},v)=f_{\theta }(s)\text{ and }l=(z-v{)}^2-{\pi }^{\mathrm{T}}\log \mathbf{p}+c\Vert \theta {\Vert }^2$$
其中l是损失函数。z是实际价值，v是网络输出的价值，p是网络输出的策略概率，π是通过MCTS修正过的策略，c是正则化项，用以约束网络参数，防止过拟合。

训练&分析

在整个训练过程中，共生成了490万次自我对弈，每个MCTS使用1600次模拟，相当于每次移动大约0.4 s的思考时间。

图-3分别对比了，AlphaGo Lee，强化学习 Zero，以及在一开始使用有监督学习的强化学习，随着学习时间增加的模型效果，子图a中Elo rating是用于评价棋手水平；子图b用于预测人类棋手动作；子图c用于预测谁能获胜。

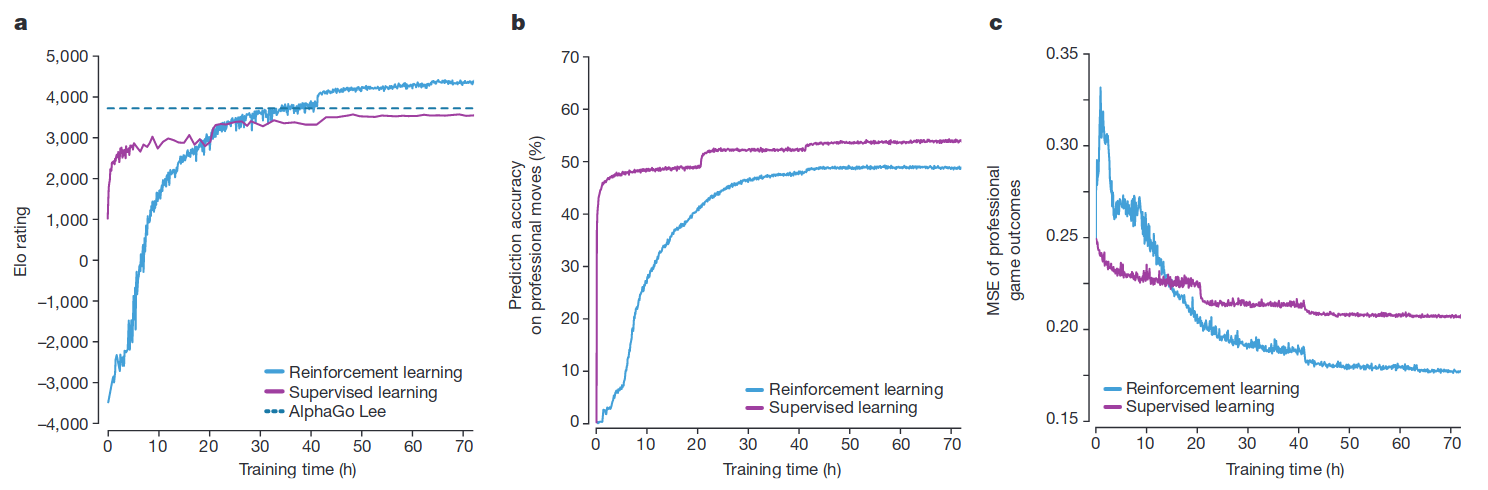
Alpha Zero仅用了36 小时就超过了Alpha Lee，72小时后完胜。相比之下，Alpha Zero使用4个TPU的单机，Alpha Lee分布在多台机器上，经过了几个月的训练。

比较出人意料的是，前期向专家学习反而限制了最终模型的效果；另外，和专家学习能更好地预测人的动作，但不能达到最好的效果，似乎说明学习专家反而抑置机器的表现（不过，我觉得这可能和计算U时的N有关，也是可改进的）。

作者还实验了修改网络结构对模型的影响，发现加入残差层和神经网络二合一分别提升了模型效果。

学到的知识和最终效果

AlphaGo Zero从完全随机的动作迅速发展到对围棋概念的复杂理解，包括引信、战术、生死、ko 、yose、捕获比赛、哨兵、形状、影响和领地……
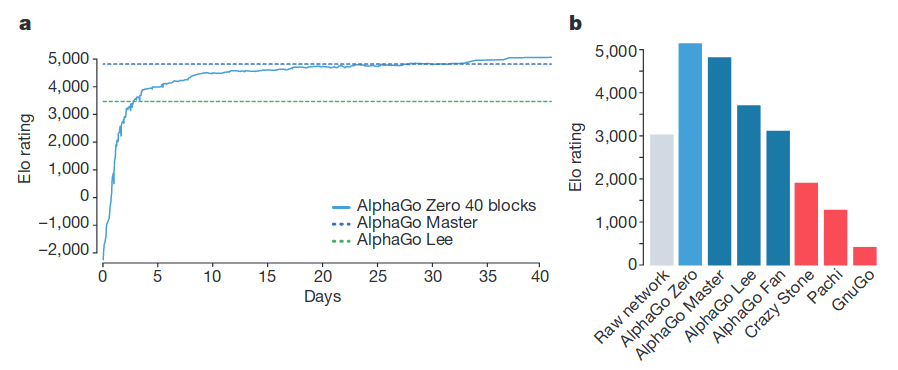
图-6展示了Zero与其它模型的对比效果，Elo rating中200分的差距对应75 %的获胜概率。