目录
一、前言
二、计数原理
1、加法原理
2、分割立方体(lanqiaoOJ题号1620)
3、乘法原理
4、挑选子串(lanqiaoOJ题号1621)
5、糊涂人寄信(lanqiaoOJ题号1622)
6、战斗吧N皇后(lanqiaoOJ题号1623)
三、鸽巢原理
1、鸽巢原理概念
2、小蓝吃糖果(lanqiaoOJ题号1624)
四、二项式定理与杨辉三角
1、概念
2、杨辉三角形(2021年省赛,lanqiaoOJ题号1457)
一、前言
本文主要讲了计数原理、鸽巢原理、杨辉三角的概念与相关编程题。
二、计数原理
1、加法原理
- 加法原理:集合 S 被分成两两不相交的部分 S1、S2、S3、..、Sm,那么 S 的对象数目等于:|S| = |S1| + |S2| + |S3| + ... + |Sml
- 例:一个学生想学一门数学课,一门文化课,但不能同时选,现在从 4 门数学课和 4 门文化课中选,一共有 4+4=8 种方法选一门课。
- 加法原理的关键是将计数分解为若干个独立(不相容)的部分,保证既不重复也不遗漏地进行计数。
2、分割立方体(lanqiaoOJ题号1620)
【题目描述】
一个立方体,边长为 n,分割成 n×n×n 个单位立方体。任意两个单位立方体,或者有 2 个公共点,或者有 4 个公共点,或者没有公共点。请问,没有公共点和有 2 个公共点的立方体,共有多少对?
【输入描述】
一个整数n, 1<=n<=30
【思路】
反过来计算,先算出有 4 个公共点的立方体有多少对,然后用总对数减去。分几种情况讨论:
1) 正方体和周围 3 个正方体相邻,这种情况共有 8 个,就是顶角上的 8 个,总个数 3×8;
2) 正方体和周围 4 个正方体相邻,这种情况共有 (n-2)×12 个,总个数 4×(n-2)×12;
3) 正方体和周围 5 个正方体相邻,这种情况共有 6×(n×n-4×n+4) 个,总个数 5×6×(n×n-4×n+4);
4) 正方体和周围 6 个正方体相邻,这种情况共有 (n×n×n-n×n×6+n×12-8) 个,总个数 6×(n×n×n-n×n×6+n×12-8);
最后把这 4 个情况求和再除以 2。
正方体一共 n^3 个,共有 n^3(n^3-1)/2 种关系。
n=int(input())
if n==1:
print(0) #边长为1时特判
else:
sum=n*n*n*(n*n*n-1)//2 #总数
edge3=8
ans3=3*edge3
edge4=(n-2)*12
ans4=4*edge4
edge5=n*n-4*n+4
ans5=5*6*edge5
edge6=n*n*n-n*n*6+n*12-8
ans6=6*edge6
print(sum-(ans3+ans4+ans5+ans6)//2)
3、乘法原理
- 令 S 是对象的有序对 (a,b) 的集合,其中第一个对象 a 来自大小为 p 的一个集合,对于对象 a 的每个选择,对象 b 有 q 个选择,那么 S 的大小:ISI-p×q
- 例:中性笔的长度有 3 种,颜色有 4 种,直径有 5 种。不同种类的中性笔有:3×4×5=60 种。
- 例:3^4×5^5×7^2×11^3的正整数因子有多少? 答: 这是算数基本定理的概念。3 有 0-4 这 5 种选择,5 有 6 个选择,7 有 3 个选择,11 有 4 个选择,因子总数是 5×6×3×4=360 种。
【排列数】
排列是有序的。
- 不可重复排列数:从 n 个不同的物品中取出 r 个,排列数为:
- P(n, r) = n(n- 1)(n - 2)...(n-r+1) = n!/(n-r)!
- 可重复排列数,从 n 个不同的物品中可重复地取出 r 个的排列数为:n^r
【组合数】
排列是有序的,组合是无序的。如果 S 中的元素都不相同,组合数:
4、挑选子串(lanqiaoOJ题号1621)
【题目描述】
有 n 个数,和一个整数 n。从这 n 个数选出一个连续子串,要求这个子串里面有 k 个数要大于等于 m。问一共能选出多少个子串。显然子串个数要大于等于 k 个。
【输入描述】
第一行是 3 个整数 n、m、k。第二行是 n 个整数 a1、a2、...、an,表示序列。2<=n<=200000,1<=k<=n/2,1<=m, ai<=10^9
【输出描述】
输出一个整数表示答案。
【思路】
一个个地输入 ai,直到输入的数字里,大于 m 的数够 k 个,就可以开始统计了。
1)若正好到 k 个数,情况总数是:第一个大于 m 的位置 i(之前),乘以 i(当前) 以后的个数,相当于求出了这一段区间的总个数。
2)大于 k 个后,怎么求出以后的序列个数而且保证不重复呢?从前往后推理,用倒数第二个位置-倒数第一个位置的差,乘上后面的个数。(这句话需要自己琢磨一下,讲得并不清晰,最好能举一个具体的例子来说明一下)
n,m,k=map(int,input().split())
a=[0]+list(map(int,input().split()))
sum=0
d=[0]*(n+1)
t=0
for i in range(n+1):
if a[i]>=m:
t+=1
d[++t]=i #d[]: 比m大的数字所在位置。这里的++没有任何意义,python并无自增和自减
if t>=k: #首先统计出k个比m大的
if t==k:
sum+=d[1]*(n-i+1)
else:
sum+=(d[t-k+1]-d[t-k])*(n-i+1)
print(sum)
5、糊涂人寄信(lanqiaoOJ题号1622)
【题目描述】
有一个糊涂人,写了 n 封信和 n 个信封,到了邮寄的时候,把所有的信都装错了信封。求装错信封可能的种类数。
【输入描述】
每行输入一个正整数 n,表示一种情况。(n<20)
【输出描述】
输出相应的答案。
【思路】
题目建模为:有 1~n 个数字,分别放在 n 个位置,问都放错的情况有多少种。
用 DP 来做,定义 dp[],dp[i] 表示数字 1~i 都放错的种类数。dp[n] 是答案。
下面考虑状态转移方程,从 1~i 递推到 i。
数字 i 如果放错,有 i-1 个位置可以放,假设其放在第 k 个位置。对于数字 k,可以放在 i 位置也可以不放在 i 位置。
如果 k 放在 i 位置,那么对于剩下 i-2 个数字放的次数,就是 i-2 个数字都放错的方法数 dp[i-2]。
如果 k 不放在 i 位置,和 i-1 个数字放错的情况相同,为 dp[i-1]。
状态转移方程:dp[i] = (i-1)*(dp[i-1]+dp[i-2])
- 注意本题的输入:没有明确终止
- 第 6 行处理了这种情况。
import sys
def f(n):
if n==0 or n==1:
return 0
elif n==2:
return 1
else:
return (n-1)*(f(n-1)+f(n-2))
for n in sys.stdin: #读入n,和C++代码的while(cin>>n)功能一样
n=int(n)
print(f(n))
6、战斗吧N皇后(lanqiaoOJ题号1623)
【题目描述】
在一个 N*M 的棋盘中,存在多少种方式使得两个皇后可以互相攻击。
【输入】
输入有若干行,每行两个数 N,M (1<=N,M<=106)
【输出】
对于每组测试数据输出一行表示答案
【思路】
两个皇后如果能攻击,位于同一行、同一列、同一对角线。
设矩阵为 n*m,前 2 者的可能性是 (m+n-2)*n*m。(同一行:n*m*(m-1);同一列:m*n*(n-1))
其他情况请自己思考。(对角线情况)
注意本题的输入没有明确终止,且每行读取 2 个数。第 2~4 行处理了这种输入的情况。
import sys
for line in sys.stdin: #读多个数,和C++的while(cin>>n>>m)功能一样
n=int(line.split()[0])
m=int(line.split()[1])
if n>m:
n,m=m,n
if n==1:
print(m*(m-1))
continue
ans=m*n*(m+n-2)
ans+=2*(n-2)*(n-1)*(2*n-3)//3
ans+=2*(m-n+1)*n*(n-1)
print(ans)
三、鸽巢原理
1、鸽巢原理概念
鸽巢原理,又称抽屉原理。
鸽巢原理:把 n+1 个物体放进 n 个盒子,至少有一个盒子包含 2 个或更多的物体。
例:在370人中,至少有2人生日相同;
答:把365天看成365个抽屉。把365人放进365个抽屉,不管怎么放,抽屉里面都有人了。
例:n个人互相握手,一定有2个人握手次数相同
答:每人跟其他人握手,最少可以是 0 次,最多可以是 n-1 次。
如果握手最少的是 0 次,那么剩下的 n-1 人中,握手最多的人不会超过 n-2 次。0~n-2 共 n-1 种情况。
如果握手最少的张三是 1 次,那么剩下的 n-1 人中,握手最多的李四除了跟张三握手一次,跟其他 n-2 人最多握手 n-2 次,李四最多握手 n-1 次。1~n-1 共 n-1 种情况。
如果握手最少的张三是 2 次,那么剩下的 n-1 人中,握手最多的李四除了跟张三握手一次,跟其他 n-2 人最多握手 n-2 次,李四最多握手 n-1 次。
2~n-1 共 n-2 种情况。
所以握手次数最多有 n-1 种情况,最少只有 1 种情况。
把最多的 n-1 种情况看成 n-1 个抽屉,n 个人放进这 n-1 个抽屉,至少有一个抽屉里面有 2 人。
2、小蓝吃糖果(lanqiaoOJ题号1624)
【题目描述】
Gardon有 n 种糖果,每种数量已知。Gardon 不喜欢连续 2 次吃同样的糖果。问有没有可行的吃糖方案。
【输入】
第一行是整数 N,O<n<1000000,第二行是 n 个数,表示 n 种糖果的数量 mi,0<mi<1000000
【输出】
输出一行,包含一个 "Yes" 或 "no"。
【思路】
鸽巢原理,用 “隔板法” 求解。
找出最多的一种糖果,把它的数量 K 看成 K 个隔板,隔成 K 个空间(把每个隔板的右边看成一个空间);其它所有糖果的数量为 S。
最多的一种糖果,把它的数量 K 看成 K 个隔板,隔成 K 个空间 (把每个隔板的右边看成一个空间);其它所有糖果的数量为 S。
1)如果 S<K-1,把 S 个糖果放到隔板之间,这 K 个隔板不够放,必然至少有 2 个隔板之间没有糖果,由于这 2 个隔板是同一种糖果,所以无解。
2)S>=K-1时,肯定有解。其中一个解是:把 S 个糖果排成一个长队,其中同种类的糖果是挨在一起的,然后每次取 K 个糖果,按顺序一个一个地放进 K 个空间。由于隔板数量比每一种糖果的数量都多,所以不可能有 2 个同样的糖果被放进一个空间里。把 S 个糖果放完,就是一个解,一些隔板里面可能放好几种糖果。
n=int(input())
a=list(map(int,input().split()))
if sum(a)-max(a)<max(a)-1:
print("No")
else:
print("Yes")四、二项式定理与杨辉三角
1、概念
杨辉三角:排列成如下三角形的数字
每个数是它上面 2 个数的和。
求杨辉三角第 n 行的数字,可以模拟这个推导过程,逐级递推,复杂度 O(n^2)。用数学公式计算,可以直接得到结果,这个公式是 (1 +x)^n。
二项式系数就是 (1+x)^n 展开后第 r 项的系数。
理解:(1+x)^n 的第 r 项,就是从 n 个 x 中选出 r 个,这就是组合数的定义
当 n 较大,且需要取模时,二项式系数有两种计算方法:
1)递推公式:
公式是杨辉三角的定义,即 “每个数是它上面 2 个数的和” 。计算复杂度是 O(n^2)。
2)用逆直接计算因为输出取模,那么不用递推公式,直接用公式计算更快。不过,由于除法不能直接取模,需要用到逆。用逆计算二项式系数,有:
用逆计算二项式系数,复杂度是 O(n) 的。
2、杨辉三角形(2021年省赛,lanqiaoOJ题号1457)
【题目描述】
如果我们按从上到下、从左到右的顺序把杨辉三角形的所有数排成一列,可以得到如下数列:1, 1, 1, 1, 2, 1, 1, 3, 3, 1, 1, 4, 6, 4, 1, ...。给定一个正整数 N,请你输出数列中第一次出现 N 是在第几个数?
【输入描述】
输入一个整数 N。 N<=1000000000
【输出描述】
输出一个整数表示答案。
- 直接计算杨辉三角的每个数,然后推导出 N 的位置。上一行的 2 个数相加得下一行的一个数。例如上一行是 b[0]~b[k],下一行是 a[0]~a[k+1],那么 a[i] = b[i-1] + b[i]。
- 推算过程只用一个数组完成,和 DP 的自我滚动数组的原理一样,即 a[i] = a[i-1] + a[i]
def f():
n=int(input())
a=[0]*100050
sum=0 #sum等于1~line行的数字个数
line=0
sum,a[0]=1,1
if n==1:
print(1)
return
for line in range(1,50000): #line: 杨辉三角的第line行
for i in range(line,0,-1): #倒过来循环,和DP的自我滚动数组的原理一样
a[i]=a[i-1]+a[i] #上一行的2个数相加得下一行的一个数
if a[i]==n:
print(sum+line-i+1)
return
sum+=(line+1) #1~line行的数字个数。每行比上一行多一个,累加
f()
以上,组合数学原理与例题
祝好

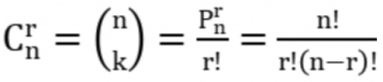


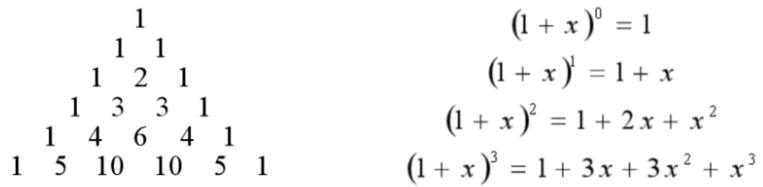
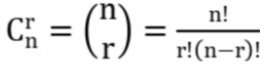

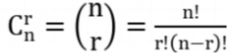
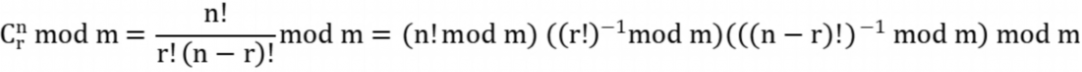





![[LeetCode周赛复盘] 第 333 场周赛20230219](https://img-blog.csdnimg.cn/29f6f204ccfb4ecf90a7b04f6c94d905.png)