自古逢秋悲寂寥，我言秋日胜春朝

二叉树结构说明

本博客使用树节点结构，如下所示：

Kotlin 版本

class TreeNode(var value: String, var leftNode: TreeNode? = null, var rightNode: TreeNode? = null)

Java 版本

class TreeNode(){
    public int value;
    public TreeNode rightNode;
    public TreeNode leftNode;
}

树

定义：树（Tree）是n（n>=0）个节点的有限集合。当n=0时，它为空树，否则为非空树。

对于非空树：

• 有且只有一个根节点
• 除根结点以外的其余结点可分为k（k>0）个互不相交的有限集T1，T2，…，T，其中每一个集合本身又是一棵树，并且称为根的子树（SubTree）。

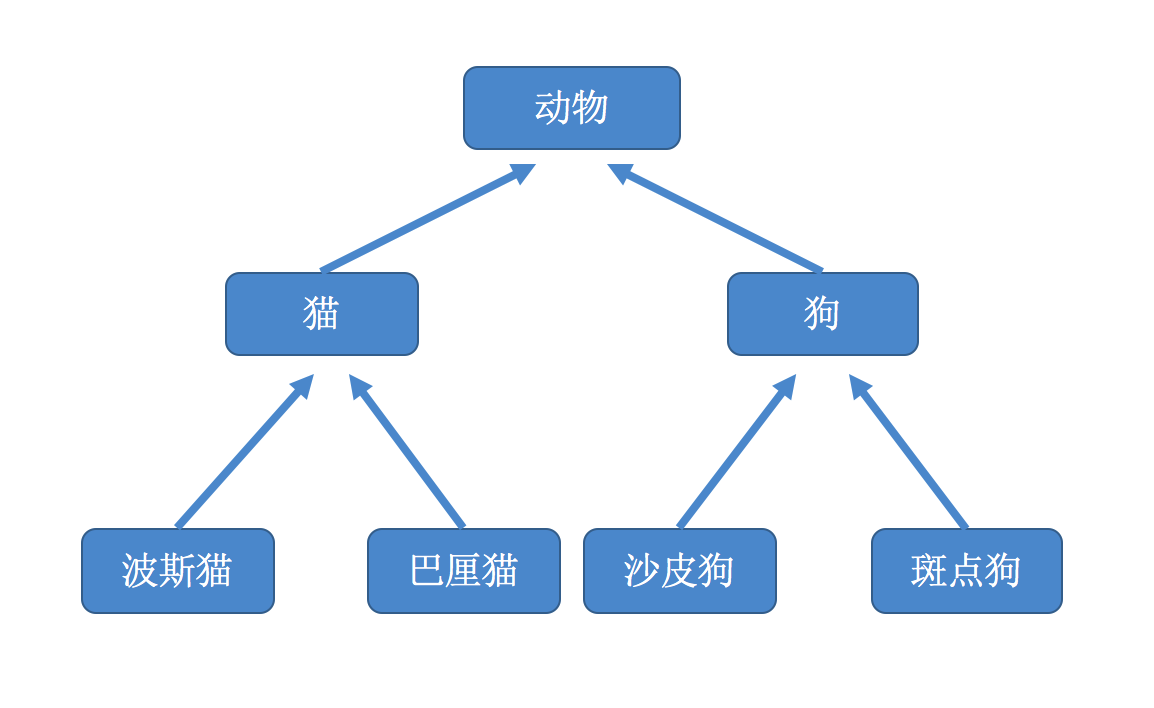
树的基本术语

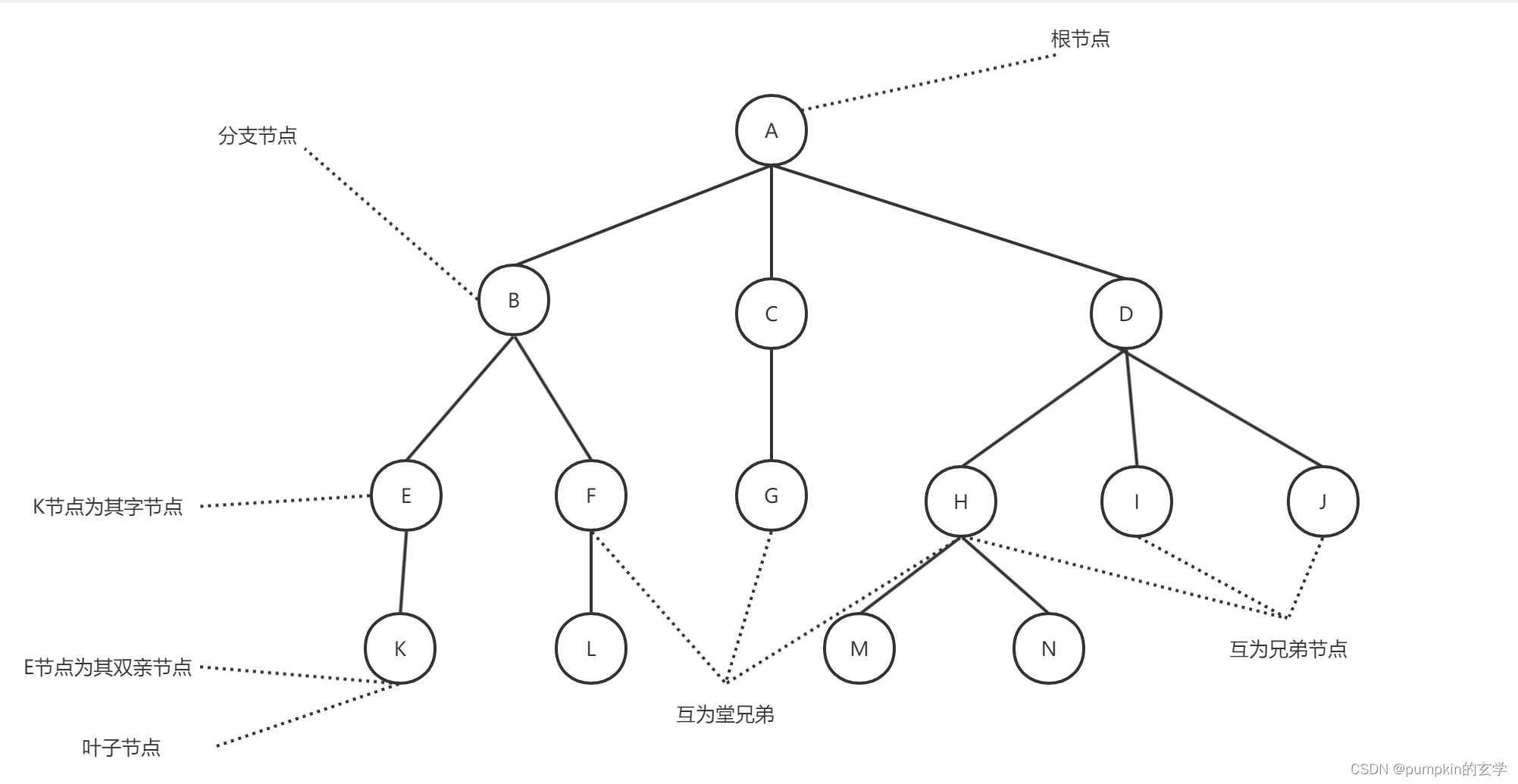
• 结点：树中的一个独立单元。包含一个数据元素及若干指向其子树的分支，如上图中的A、B、C、D等。
• 结点的度：结点拥有的子树数。例如，A的度为3，B的度为2，F的度为1，G的度为0。
• 树的度：树的度是树内各结点度的最大值。上图中所示的树的度为3
• 叶子：度为0的结点称为叶子或终端结点。结点K、L、G、M、I、J都是树的叶子。
• 非终端结点：度不为0的结点称为非终端结点或分支结点。除根结点之外，非终端结点也称为内部结点。
• 双亲和孩子：结点的子树的根称为该结点的孩子，相应地，该结点称为孩子的双亲。例如，上图的E节点和K节点。
• 兄弟：同一个双亲的孩子之间互称兄弟。例如，H、I和J互为兄弟。
• 堂兄弟：双亲在同一层的结点。例如，结点F、G、H互为堂兄弟。
• 祖先：从根到该结点所经分支上的所有结点。例如，M的祖先为A、D和H.
• 子孙：以某结点为根的子树中的任一结点都称为该结点的子孙。如B的子孙为E、K、L和F。
• 层次：结点的层次从根开始定义起，根为第一层，根的孩子为第二层。树中任一结点的层次等于其双亲结点的层次加1。
• 树的深度：树中结点的最大层次称为树的深度或高度。图中所示的树的深度为4
• 有序树和无序树：如果将树中结点的各子树看成从左至右是有次序的（即不能互换），则称该树为有序树，否则称为无序树。在有序树中最左边的子树的根称为第一个孩子，最右边的称为最后一个孩子。

上述树的概念了解一下即可，主要是二叉树以及红黑树。

二叉树

介绍

二叉树：是每个节点最多有两颗子树的树结构。通常被称作左右子树。

性质：

• 二叉树的每个节点至多只有两颗子树（不存在度数大于2的结点）。其子树有左右之分。
• 二叉树第i层最多有2^(i-1)个节点。
• 深度为k的二叉树最多有2^k-1个节点。

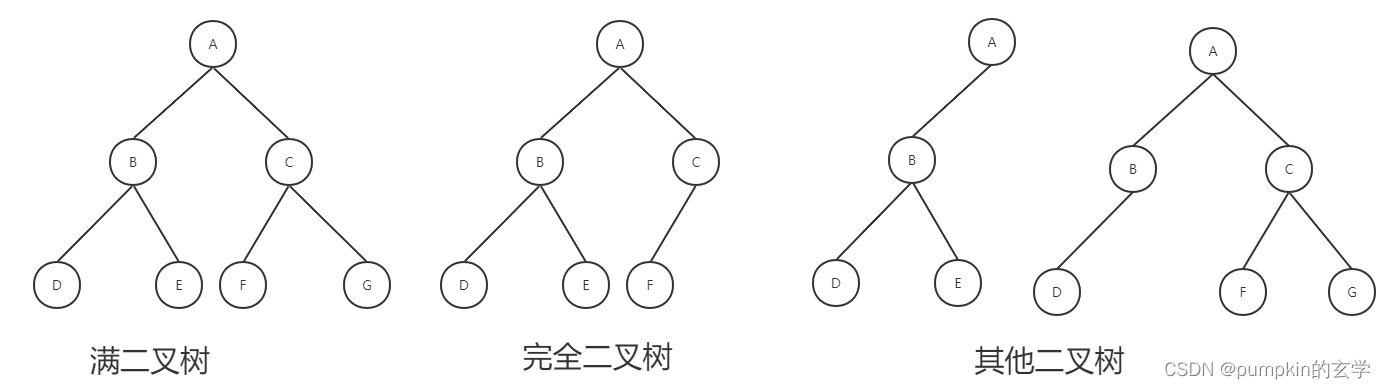
满二叉树：一颗深度为K的二叉树且有2^k-1个节点。

完全二叉树：一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。

二叉树深度优先搜索

对于二叉树来说，常用深度优先搜索进行遍历。其又可以细分为前序遍历、中序遍历以及后序遍历。

对于如下一颗二叉树，其前序、中序、后序遍历结果如下：

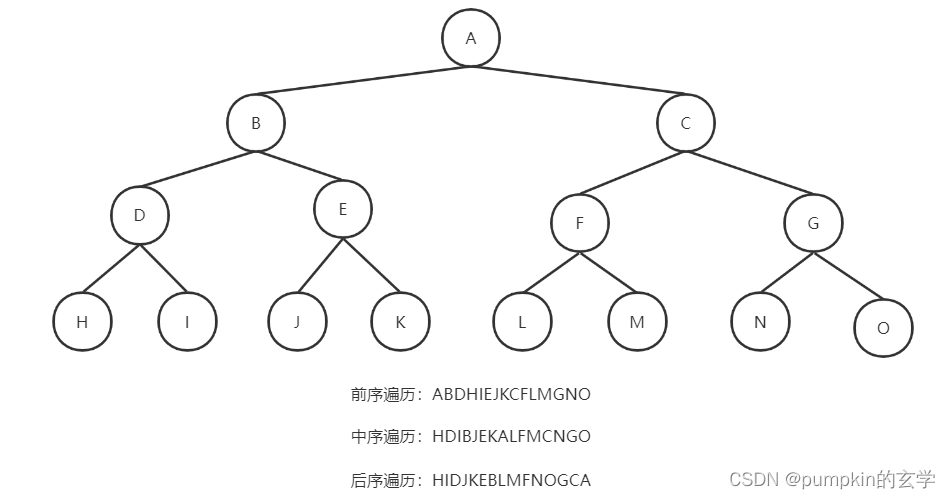
下面对上述前序、中序、后序遍历进行详细解析。

前序：

动图演示：

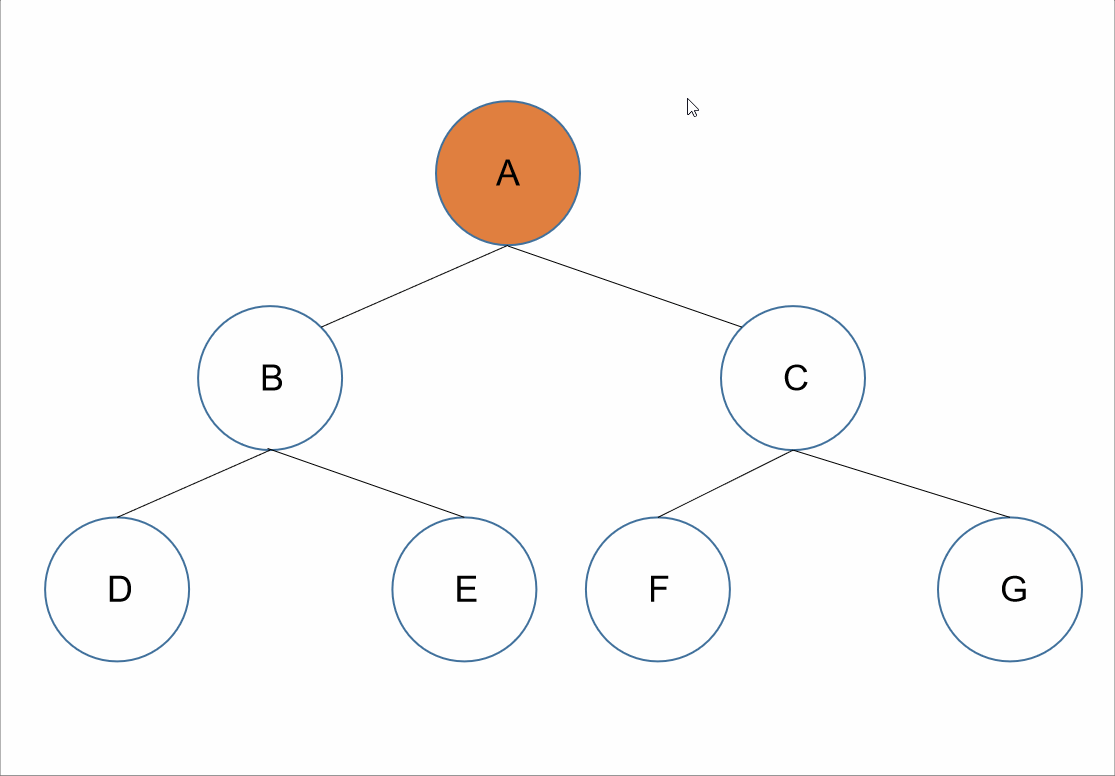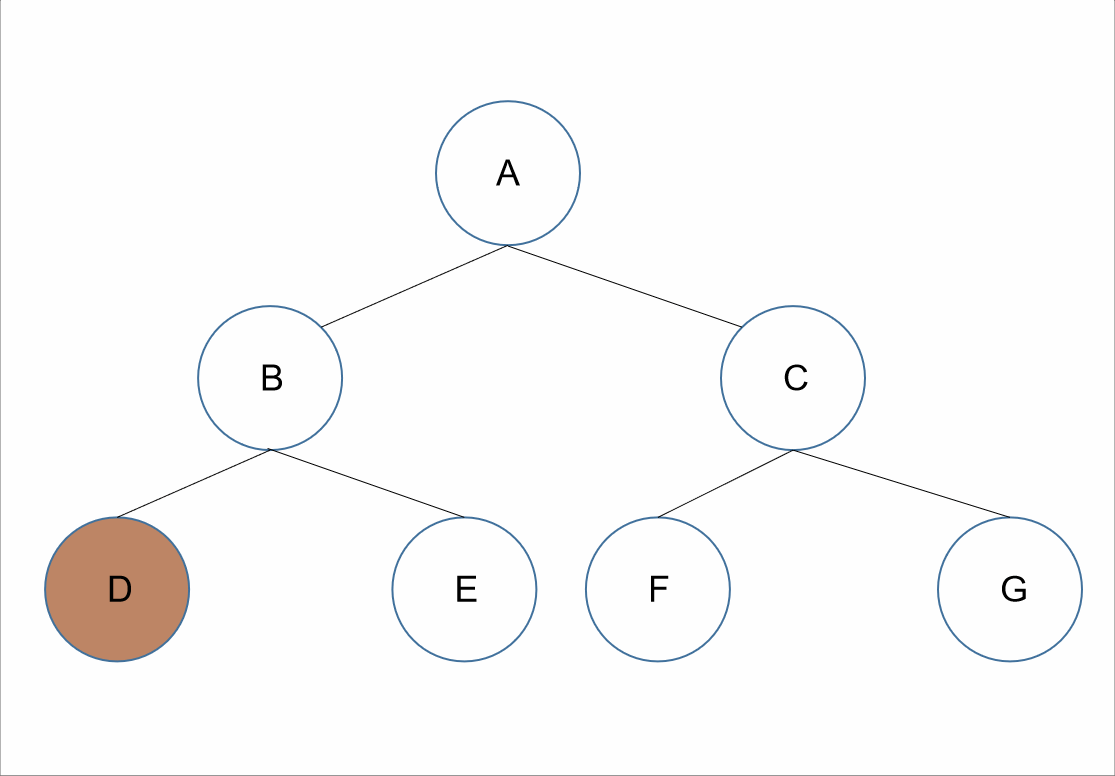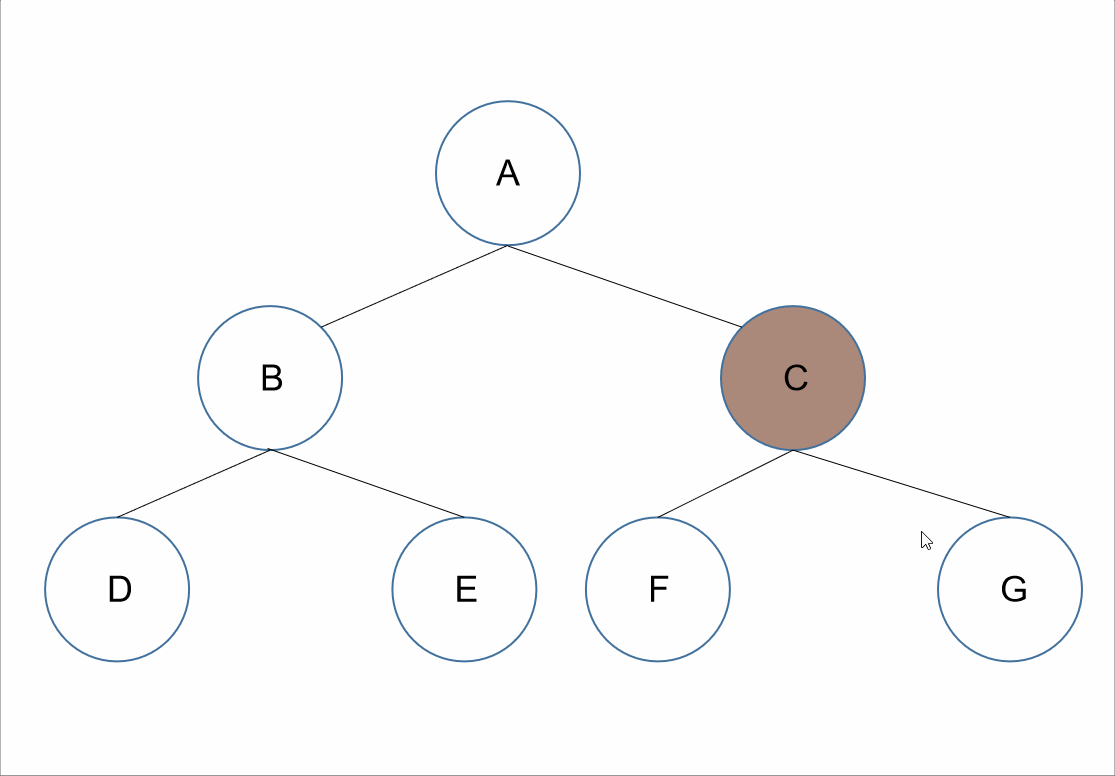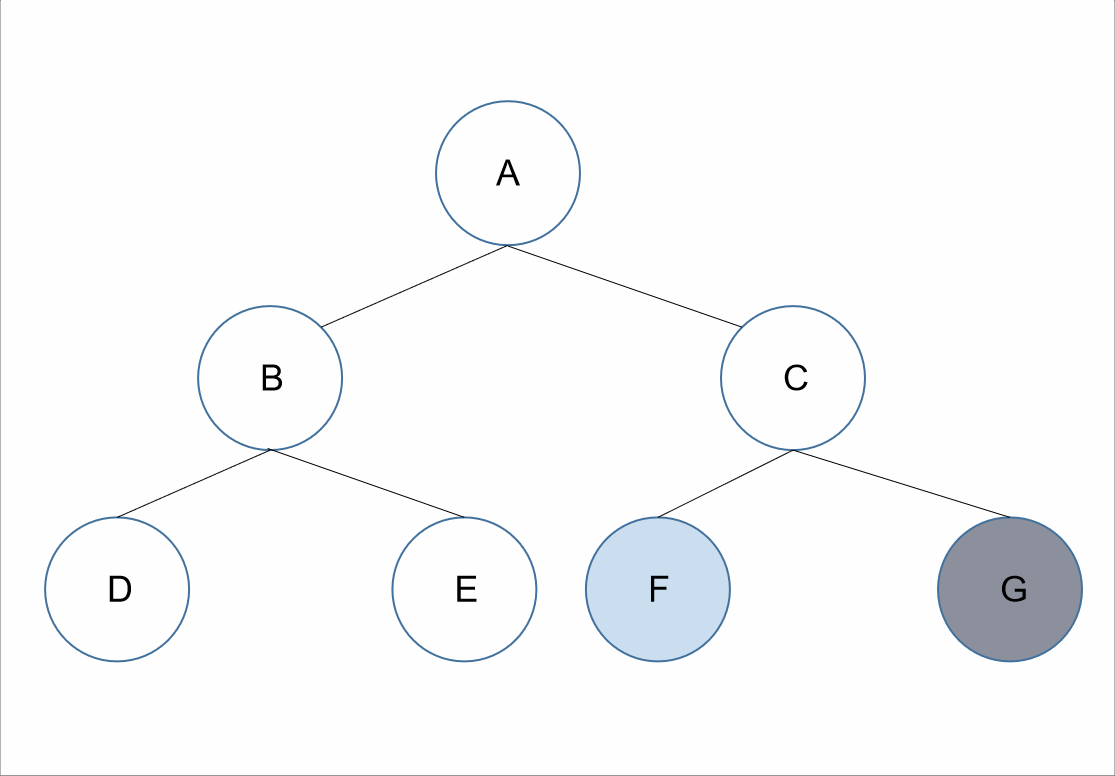
遍历顺序为：跟左右。

在整棵树的遍历过程中，先获取其根节点的值，接着为其左节点的值，之后为其右节点的值。

对于上述的树来说，所以我们先获取到根节点的值为A，接下来遍历A的左节点，B节点，所以我们可以获取到B节点的值B；但是对于结点B、D、E来说，节点B是它们的根节点，所以根据跟左右接下需要遍历的是B节点的左节点，D节点，可以获取到值D。如果我们把D节点当作根节点来看的话，因为D节点没有左右节点，我们可以默认D节点的跟左右已经走完了。所以我们回到D节点的父节点B节点。对于B节点来说，此时已经遍历了根左，接下来就是其右节点E节点。我们遍历E节点获取其值E。此时对于A节点来说，其左子树已经遍历完了，根据跟左右，我们遍历器右子树，和前面遍历类似，我们可以获取到值C、F、G。

所以最终前序遍历的结果为：A、B、D、E、C、F、G

代码说明

遍历二叉树之前，我们先构造一个二叉树，后续不同的遍历方式，均调用该函数构造一个上图所示的二叉树。

Kotlin 版本

object Helper {
    /**
     * 创建二叉树
     */
    fun createBinaryTree(): TreeNode {
        return TreeNode(
            value = "A",
            leftNode = TreeNode(
                value = "B",
                leftNode = TreeNode(value = "D"),
                rightNode = TreeNode(value = "E")
            ),
            rightNode = TreeNode(
                value = "C",
                leftNode = TreeNode(value = "F"),
                rightNode = TreeNode(value = "G")
            )
        )
    }
}

Java 版本

class Helper {
    /**
     * 创建二叉树
     */
    public static TreeNode createBinaryTree() {
        return new TreeNode(
                "A",
                new TreeNode(
                        "B",
                        new TreeNode("D", null, null),
                        new TreeNode("E", null, null)
                ),
                new TreeNode(
                        "C",
                        new TreeNode("F", null, null),
                        new TreeNode("G", null, null)
                )
        );
    }
}

递归写法

Kotlin 版本

fun binaryTreePreIterator(node: TreeNode?) {
    if (node != null) {
        println(node.value)
        binaryTreePreIterator(node.leftNode)
        binaryTreePreIterator(node.rightNode)
    }
}

//使用
binaryTreePreIterator(Helper.createBinaryTree())
//结果
A B D E C F G

Java 版本

    void binaryTreePreIterator(TreeNode node) {
        if (node != null) {
            System.out.printf(node.getValue());
            binaryTreePreIterator(node.getLeftNode());
            binaryTreePreIterator(node.getRightNode());
        }
    }

前序遍历的递归写法非常简单，根据跟左右的形式，依次进行递归调用即可。

非递归写法

那么如何将上述递归代码改造成非递归的写法呢？

递归很好理解在于，比如此时将父节点的左子树遍历完成之后，可以自己回到父节点遍历的函数处，接着执行遍历其右节点。

所以如果想要改造成非递归函数，则必须有一个数据结构用来记录节点的遍历信息，需要将未遍历完的节点按照执行顺序存起来。这里我们使用栈来进行保存。

fun binaryTreePreIteratorByStack(node: TreeNode?): ArrayList<String> {
    val result = ArrayList<String>()

    val stack = java.util.ArrayDeque<TreeNode>()
    var currentNode = node;
    while (currentNode != null || !stack.isEmpty()) {
        while (currentNode != null) {
            result.add(currentNode.value)
            stack.push(currentNode)
            currentNode = currentNode.leftNode
        }
        currentNode = stack.pop().rightNode
    }

    return result
}

//使用
binaryTreePreIteratorByStack(Helper.createBinaryTree()).forEach {
    println(it)
}
//结果
A B D E C F G

Java 版本

ArrayList<String> binaryTreePreIteratorByStack(TreeNode node) {
        ArrayList<String> result = new ArrayList<>();

        ArrayDeque<TreeNode> stack = new ArrayDeque <> ()
        TreeNode currentNode = node;
        while (currentNode != null || !stack.isEmpty()) {
            while (currentNode != null) {
                result.add(currentNode.getValue());
                stack.push(currentNode);
                currentNode = currentNode.getLeftNode();
            }
            currentNode = stack.pop().getRightNode();
        }

        return result;
    }

中序：

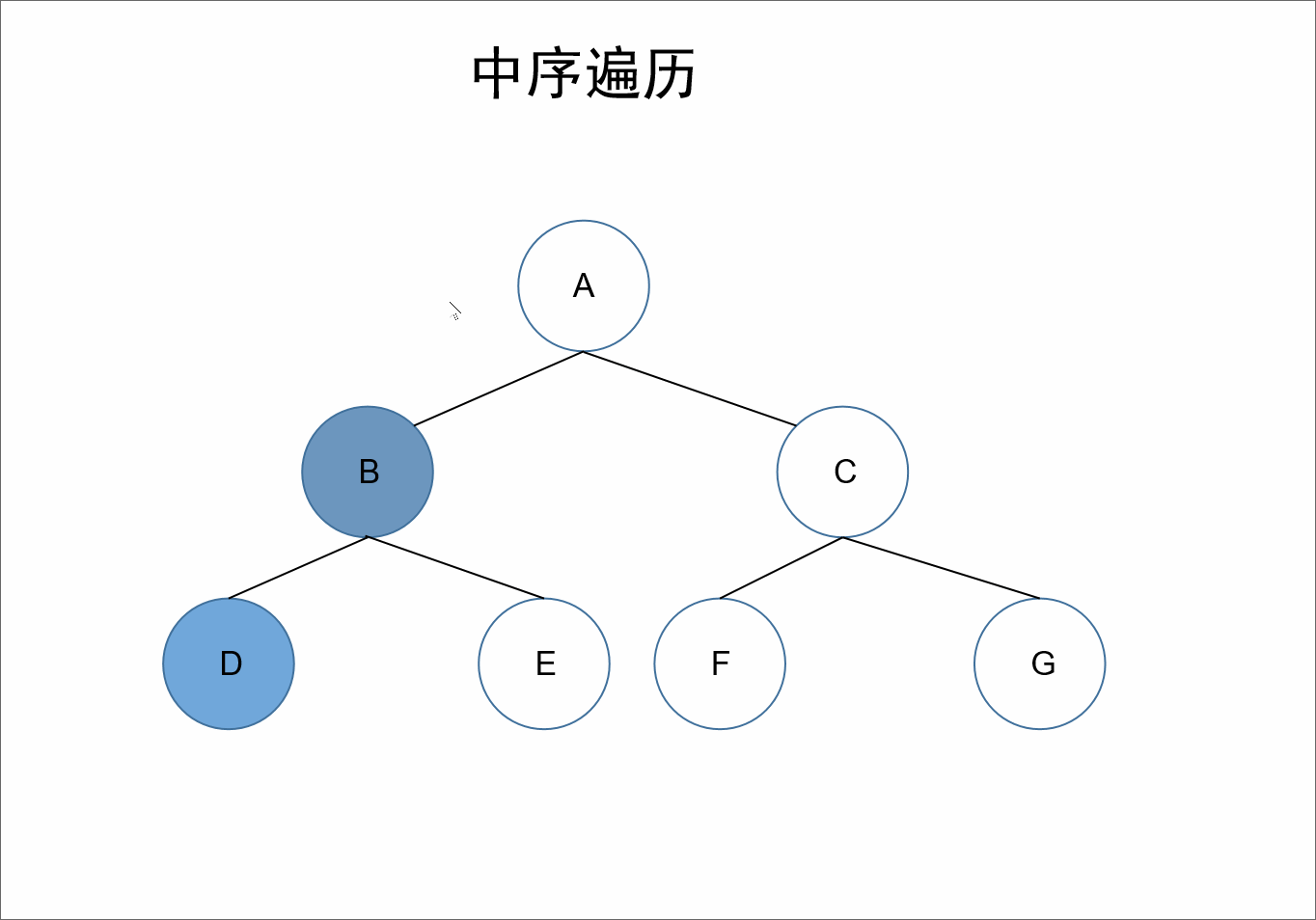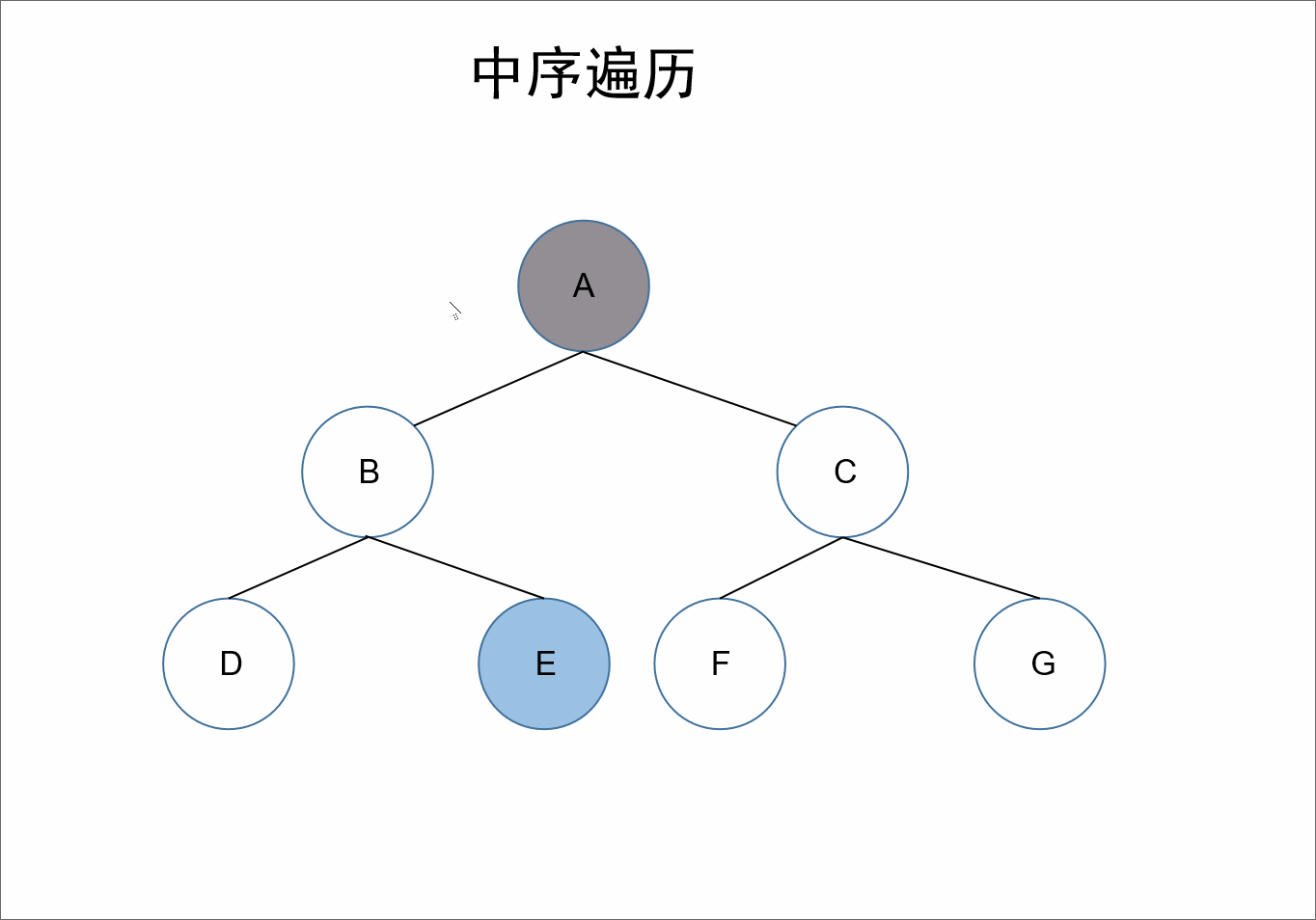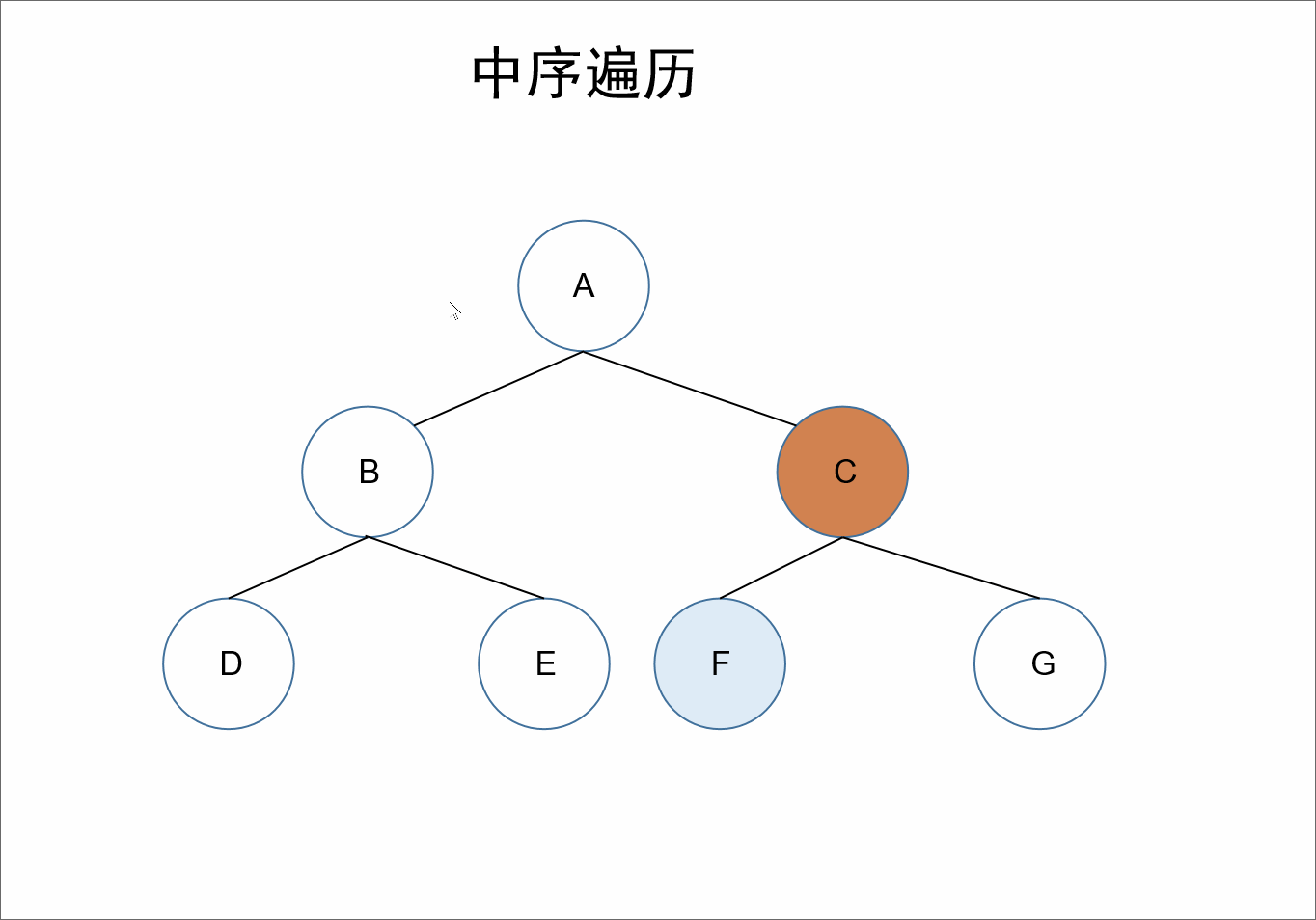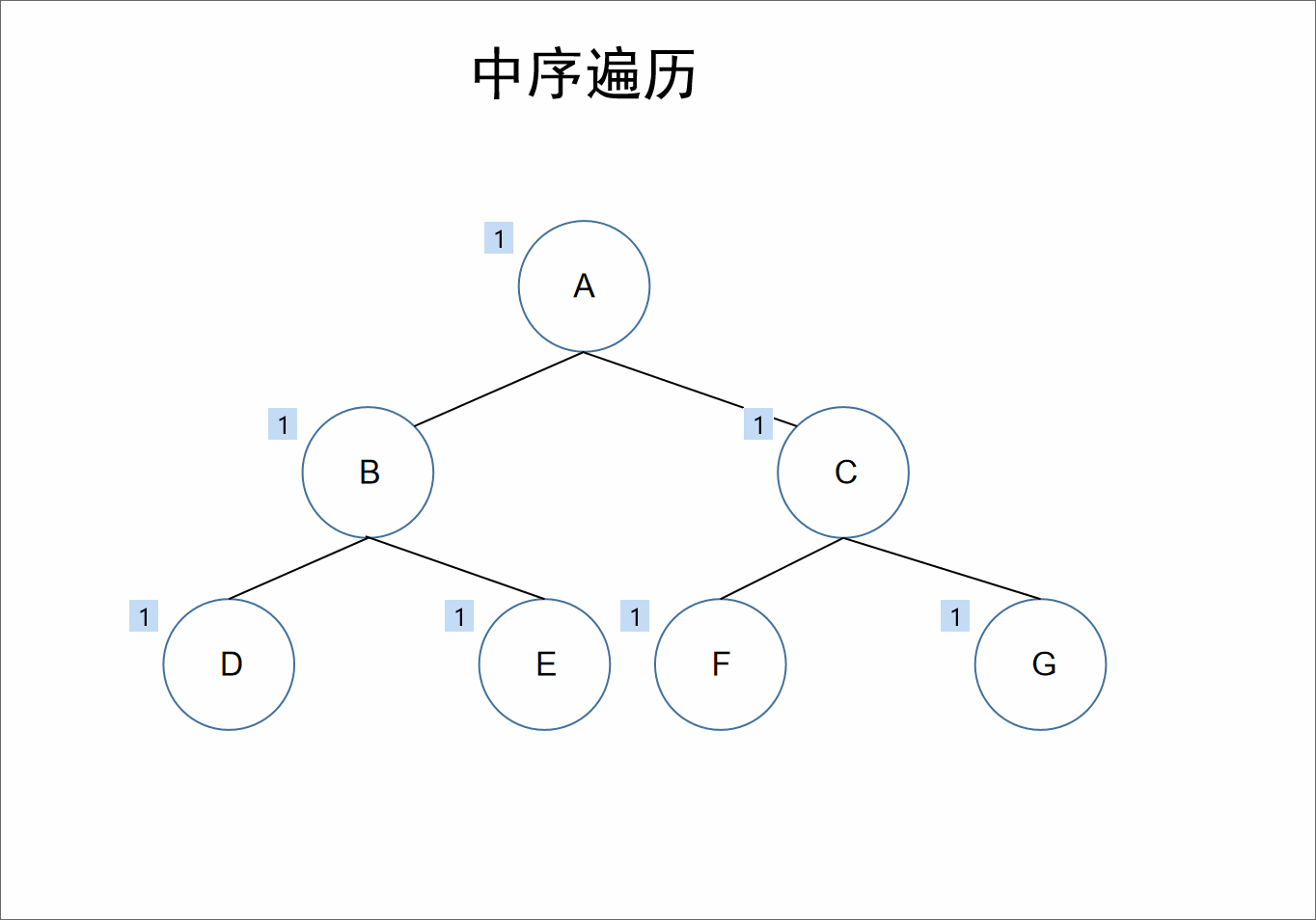
遍历顺序为：左根右。

在整棵树的遍历过程中，先遍历其左子树，之后获取自身的值，接着遍历右子树。

对于上述的树来说，A的左节点为B，对于结点B、D、E来说，节点B是它们的根节点，继续根据左根右，我们获取到D节点，接着左根右，D节点的左节点为null，接着遍历其根节点也就是自己，此时我们获取到值D，D的右节点也为null，所以对于B节点来说，其左子树也就遍历完了，接着遍历其自身可以获取到值B，接着遍历右节点E。同理对于A节点来说，其左子树遍历完毕，接着遍历其自身，获取到值A。同理遍历其右子树即可。

所以最终前序遍历的结果为：D、B、E、A、F、C、G

代码说明

递归写法：

fun binaryTreeMiddleIterator(node: TreeNode?) {
    if (node != null) {
        binaryTreeMiddleIterator(node.leftNode)
        println(node.value)
        binaryTreeMiddleIterator(node.rightNode)
    }
}
//使用
binaryTreeMiddleIterator(Helper.createBinaryTree())
//结果
D B E A F C G

Java 版本

    void binaryTreeMiddleIterator(TreeNode node) {
        if (node != null) {
            binaryTreeMiddleIterator(node.getLeftNode());
            System.out.printf(node.getValue());
            binaryTreeMiddleIterator(node.getRightNode());
        }
    }

类似于前序遍历的写法，根据左根右的形式，依次进行递归调用即可。

非递归写法：

fun binaryTreeMiddleIteratorByStack(node: TreeNode?): ArrayList<String> {
    val result = ArrayList<String>()

    val stack = java.util.ArrayDeque<TreeNode>()
    var currentNode = node
    while (currentNode != null || !stack.isEmpty()) {
        while (currentNode != null) {
            stack.push(currentNode)
            currentNode = currentNode.leftNode
        }
        val treeNode = stack.pop()
        result.add(treeNode.value)
        currentNode = treeNode.rightNode
    }

    return result
}
//使用
binaryTreeMiddleIteratorByStack(Helper.createBinaryTree()).forEach {
	println(it)
}
//结果
D B E A F C G

ArrayList<String> binaryTreeMiddleIteratorByStack(TreeNode node) {
        ArrayList<String> result = new ArrayList<>();

        ArrayDeque<TreeNode> stack = new ArrayDeque <> ()
        TreeNode currentNode = node;
        while (currentNode != null || !stack.isEmpty()) {
            while (currentNode != null) {
                stack.push(currentNode);
                currentNode = currentNode.getLeftNode();
            }
         	TreeNode treeNode = stack.pop();
       	 	result.add(treeNode.value);
        	currentNode = treeNode.rightNode;
        }

        return result;
    }

同前序遍历一样，我们使用栈保存调用顺序。之后严格根据左根右执行即可。

后序：

遍历顺序为：左右根。

在整棵树的遍历过程中，先遍历其左子树，接着遍历右子树，之后获取自身的值。

对于上述的树来说，A的左节点为B，对于结点B、D、E来说，节点B是它们的根节点，继续根据左根右，我们获取到D节点，接着左根右，D节点的左右节点为null，接着遍历其根节点也就是自己，此时我们获取到值D，所以对于B节点来说，其左子树也就遍历完了，接着遍历其右子树可以获取到E，此时对于B来说其左右子树均遍历完毕，所以我们遍历其自身即获取B。同理对于A节点来说，其左子树遍历完毕，接着遍历其右子树，可以获取到F、G、C，最后遍历自己，获取到A。

所以最终前序遍历的结果为：D、E、B、F、G、C、A

代码说明

递归写法：

fun binaryTreeAfterIterator(node: TreeNode?) {
    if (node != null) {
        binaryTreeAfterIterator(node.leftNode)
        binaryTreeAfterIterator(node.rightNode)
        println(node.value)
    }
}
//使用
binaryTreeAfterIterator(Helper.createBinaryTree())
//结果
D E B F G C A

Java 版本

    void binaryTreeAfterIterator(TreeNode node) {
        if (node != null) {
            binaryTreeAfterIterator(node.getLeftNode());
            binaryTreeAfterIterator(node.getRightNode());
            System.out.printf(node.getValue());
        }
    }

类似于前面的写法，根据左右根的形式，依次进行递归调用即可。

非递归写法

后序遍历的迭代代码要复杂一点。当达到某个节点时，如果之前还没有遍历过它的右子树就得前往它的右子节点，如果之前已经遍历过它的右子树那么就可以遍历这个节点。所以说，此时要根据它的右子树此前有没有遍历过来确定是否应该遍历当前的节点。如果此前右子树已经遍历过，那么在右子树中最后一个遍历的节点应该是右子树的根节点，也就是当前节点的右子节点。可以记录遍历的前一个节点。如果一个节点存在右子节点并且右子节点正好是前一个被遍历的节点，那么它的右子树已经遍历过，现在是时候遍历当前的节点了。

fun binaryTreeAfterIteratorByStack(node: TreeNode?): ArrayList<String> {
    val result = ArrayList<String>()

    val stack = java.util.ArrayDeque<TreeNode>()
    var currentNode: TreeNode? = node
    var preNode: TreeNode? = null
    while (currentNode != null || !stack.isEmpty()) {
        while (currentNode != null) {
            stack.push(currentNode)
            currentNode = currentNode.leftNode
        }
        currentNode = stack.peek()
        if (currentNode.rightNode != null && currentNode.rightNode != preNode) {
            //遍历右子树
            currentNode = currentNode.rightNode
        } else {
            stack.pop()
            result.add(currentNode.value)
            preNode = currentNode
            currentNode = null
        }
    }

    return result
}

     ArrayList<String> binaryTreeAfterIteratorByStack(TreeNode node) {
        ArrayList<String> result = new ArrayList<>();

        ArrayDeque<TreeNode> stack = new ArrayDeque<>()
        TreeNode currentNode = node;
        TreeNode preNode = null
        while (currentNode != null || !stack.isEmpty()) {
            while (currentNode != null) {
                result.add(currentNode.getValue());
                stack.push(currentNode);
                currentNode = currentNode.getLeftNode();
            }
            currentNode = stack.peek();
            if (currentNode.getRightNode() != null && currentNode.getRightNode() != preNode) {
                //遍历右子树
                currentNode = currentNode.getRightNode();
            } else {
                stack.pop();
                result.add(currentNode.getValue());
                preNode = currentNode;
                currentNode = null;
            }
        }

        return result;
    }

二叉树广度优先搜索

广度优先搜索，根据层级进行遍历。

可以依靠队列进行遍历。

比如对于上图所示的数据结构，广度优先搜索的遍历结果即为：A B C D E F G。

代码如下：

fun binaryTreeBreadth(node: TreeNode): ArrayList<String> {
    val result = ArrayList<String>()

    val arrayDeque1 = java.util.ArrayDeque<TreeNode>()
    val arrayDeque2 = java.util.ArrayDeque<TreeNode>()
    arrayDeque1.offer(node)
    while (!arrayDeque1.isEmpty() || !arrayDeque2.isEmpty()) {
        while (!arrayDeque1.isEmpty()) {
            val treeNode = arrayDeque1.poll()
            if (treeNode != null) {
                result.add(treeNode.value)
                val leftNode = treeNode.leftNode
                if (leftNode != null) {
                    arrayDeque2.offer(leftNode)
                }
                val rightNode = treeNode.rightNode
                if (rightNode != null) {
                    arrayDeque2.offer(rightNode)
                }
            }
        }
        while (!arrayDeque2.isEmpty()) {
            val treeNode = arrayDeque2.poll()
            if (treeNode != null) {
                result.add(treeNode.value)
                val leftNode = treeNode.leftNode
                if (leftNode != null) {
                    arrayDeque1.offer(leftNode)
                }
                val rightNode = treeNode.rightNode
                if (rightNode != null) {
                    arrayDeque1.offer(rightNode)
                }
            }
        }
    }
    
    return result
}
//使用
binaryTreeBreadth(Helper.createBinaryTree()).forEach {
	println(it)
}
//结果
A B C D E F G

下一节预告，红黑树，以及 TreeSet/TreeMap 的应用。

🙆‍♀️。欢迎技术探讨噢！