算法第四版

先导例子:动态连通性 - 书中1.5
知识点:并查集-一种用于解决动态连通性问题的算法
描述:对于N个对象,有两种操作:1.连接两个对象 2.判断两个对象是否存在连接路径
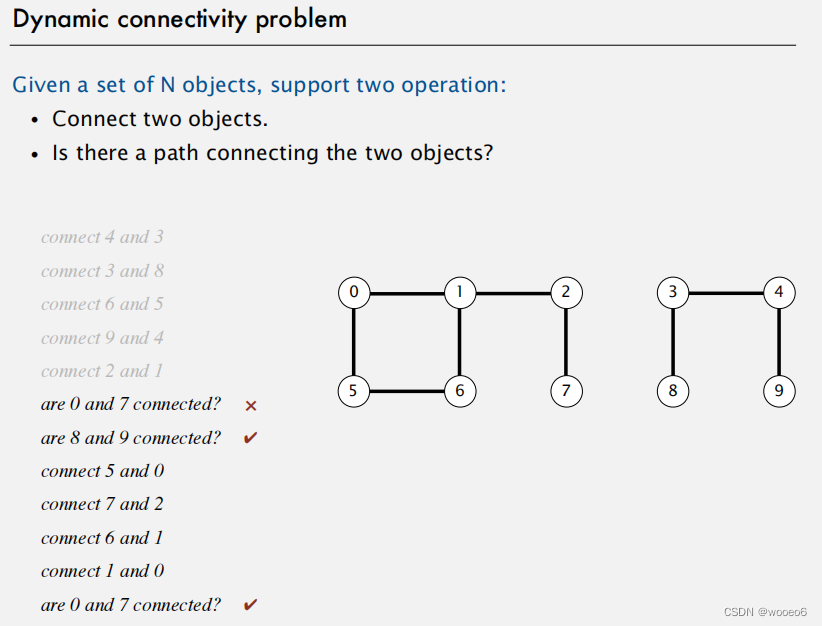
如巨大的连通性问题:
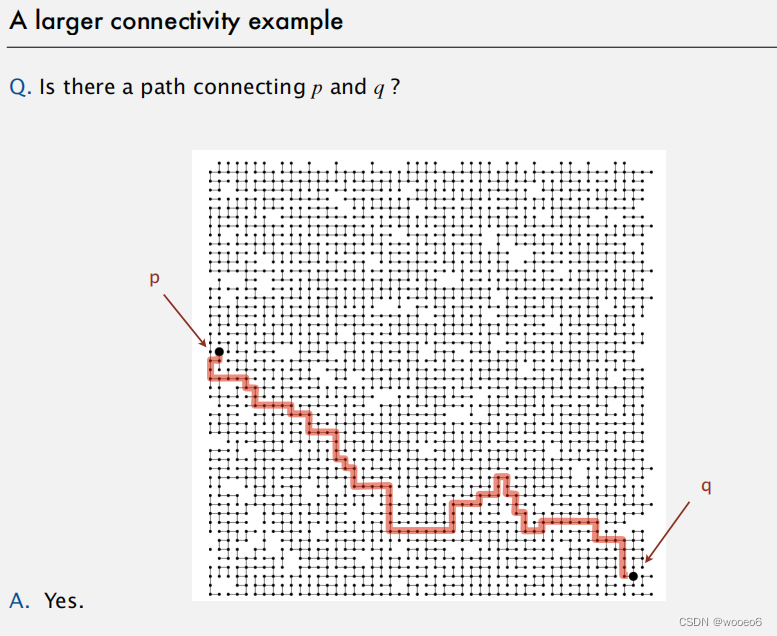
在分析问题模型时,可以先把已知的性质写出来,哪怕是显而易见的
1.对称性:如果p与q相连,则q与p连通。
2.传递性:如果p与q相连,而q与r相连,则p与r相连
定义目标的API:


客户端调用:
从标准输入中读取对象数N。
重复:从标准输入读取对整数-如果它们尚未连接,连接它们并打印对

实现及讨论历程:
原有的联合:数据结构。长度为n的整数数组id。解释: id[i]是i的父项。i的根是id[id[id[...id[i]...]]]。

步骤1.将每个对象的ID设置为其自身(N个数组访问)
步骤2.追踪父指针,直到到达根(i数组访问的深度)
步骤3.将p的根更改为指向q的根(p和q数组访问的深度)

改进1:加权。修改快速联合,以避免高大的树木。保持跟踪每棵树的大小(对象的数量)。通过连接小树的根和大树的根来实现平衡。目的是减小树的层数,避免树过高,加快寻找根的速度。
改进前后:
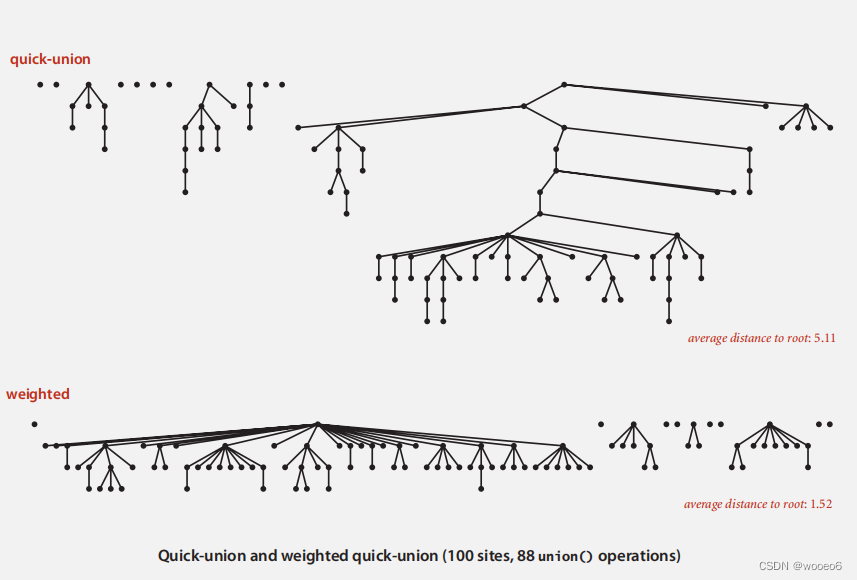
改进方法:
数据结构:与快速并集相同,但是保持额外的数组sz[i]来计算树中基于i的对象的数量。
查找/连接:与快速结合相同。
新快速联合:1.将小树的根链接到大树的根。2.更新存储存储模块数组。

改进2:路径压缩。在计算完p的根之后,将每个被检查节点的id[]设置为指向该根。
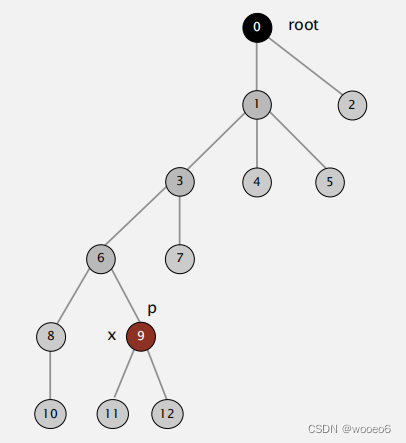
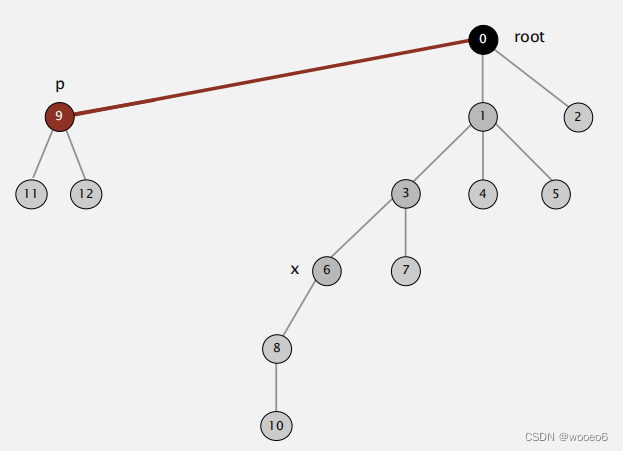
只需加入一行代码

应用
- 渗透率。
- 游戏(围棋,十六进制)。
- ✓动态连接。最不共同的祖先。
- 有限状态自动机的等价性。
- 物理学中的霍申-科佩尔曼算法。
- 欣利-米尔纳多态类型推断。
- Kruskal的最小生成树算法。
- 在Fortran中编译等价性语句。
- 形态学属性的开启和关闭。
- Matlab的bwlabel()在图像处理中的功能。
例子:渗透率
针对许多物理系统的一个抽象模型:N对N的站点网格。每个站点打开的概率为p(阻塞的概率为1-p)。
如果顶部和底部通过开放站点连接,则系统渗透。
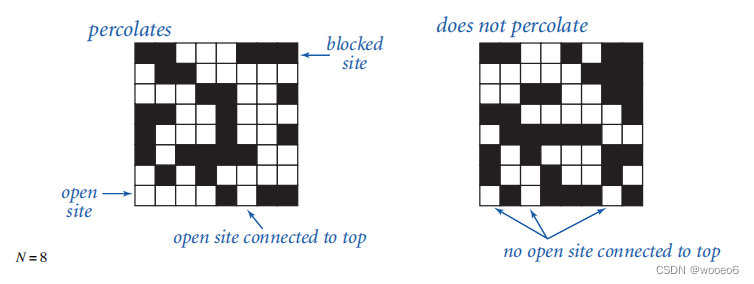
如何检查n对n系统是否渗透?模型作为一个动态连接问题,并使用联合查找

如何检查一个n-n的系统是否渗透?为每个站点创建一个对象,并将其命名为0到 N 2 – 1

如何检查一个n-n的系统是否渗透?
为每个站点创建一个对象,并将其命名为0到N2-1。
站点位于由开放的站点连接的同一组件中。
如果底部一行的任何站点都连接到顶部行的任何站点相连。(蛮力算法: N 2调用connected())
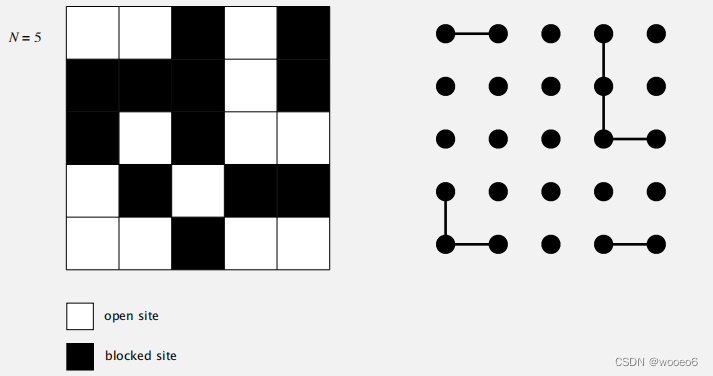
聪明的技巧:添加2个虚拟站点(以及连接到顶部和底部的连接)。如果虚拟顶部站点已连接到虚拟底部站点
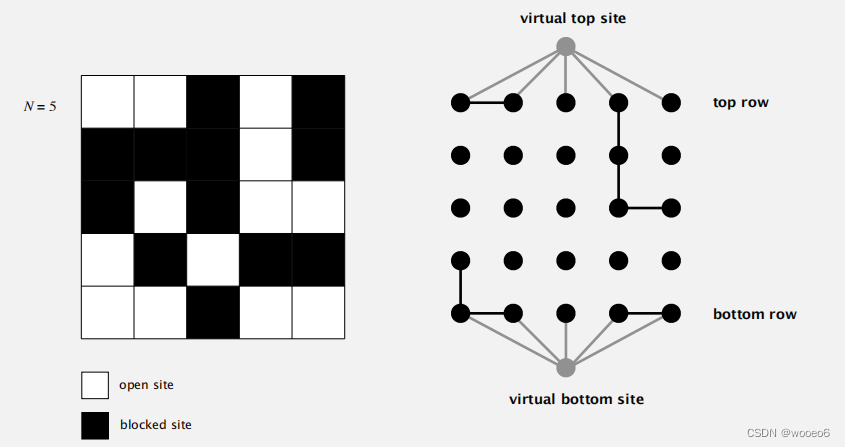
如何模拟开设一个新的站点?将新站点标记为开放站点;将其连接到所有相邻的开放站点。
算法分析 - 书中1.4
算法分析名词
最好的情况。成本的下限。由“最简单”的输入决定。为所有输入提供一个目标。
最坏的情况。成本的上限。由“最困难”的输入决定。为所有输入提供保证。
平均情况。随机输入的预期成本。需要一个“随机”输入的模型。提供了一种预测性能的方法
我们的目标:确定问题的“困难”。开发“最优”算法。
方法抑制分析中的细节:分析“在一个常数因素范围内”。消除输入模型中的可变性:关注最坏的情况。
上限,算法对任何输入的性能保证。
下界,证明没有任何算法能做得更好。
最优算法:下界=上界(在常数因子内)。
3-SUM问题实例
主要是讲算法性能的分析,重点看一个例子
3-SUM:给定N个不同的整数,有多少三数之和恰好为零?
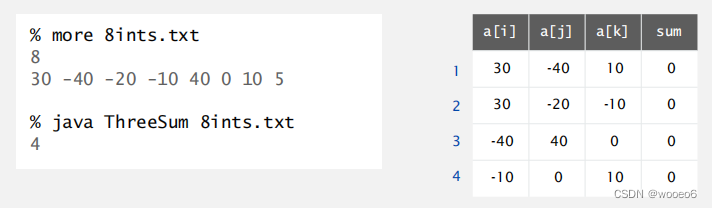
这个例子与计算几何学中的问题密切相关。
蛮力算法
检查每三个。为简单起见,请忽略整数溢出
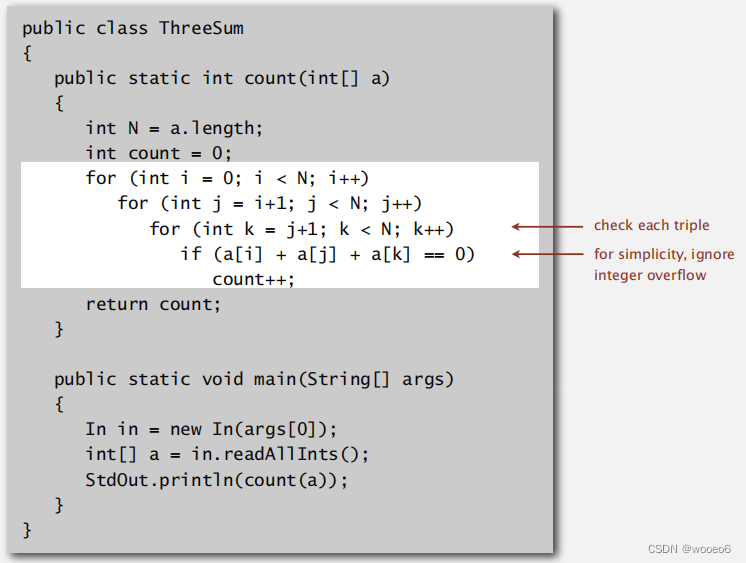
现在不知道3-SUM的更好方法,先看另两个例子,1-SUM,2-SUM
1-SUM
1-SUM:给定N个不同的整数,有多少1数之和恰好为零?
有多少条指令作为输入大小N的函数?N次访问

2-SUM
2-SUM:给定N个不同的整数,有多少2数之和恰好为零?
有多少条指令作为输入大小N的函数?N2次访问

3-SUM性能分析
大约有多少次数组访问作为输入大小N的函数?N3次访问
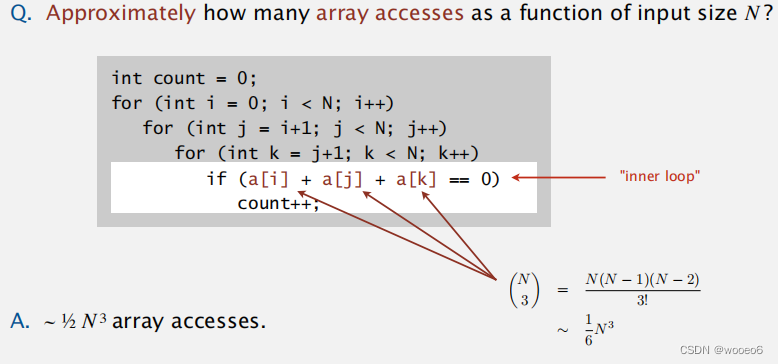
2-SUM,3-SUM快速解法
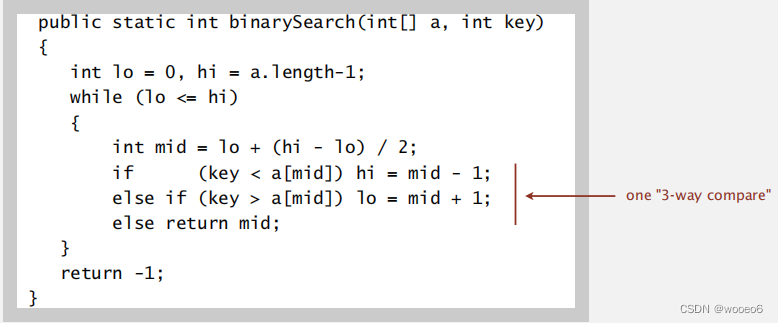
二叉搜索,首先将数组排序,O(N log N),在用二叉搜索,整体性能,O(N log N)
下面代码是二叉搜索的非递归实现,虽然二叉搜索是个简单的算法,却是众人皆知很难把每个细节实现正确的,实际上直到1962年才发表第一个没有错误的二叉搜索算法,所以我们在开发算法是要极其小心。
3-SUM算法步骤
1:对N个(不同的)数字进行排序。
2:对于每一对数字a和a[j],二进制搜索-(a[i] + a[j])。只有当a[i]
分析。增长顺序为N 2 log N。
步骤1:插入排序N2。
步骤2:加二叉搜索N 2 log N

栈和队列 - 书中1.3
单独的接口和实现
Ex:堆栈、队列、包、优先级队列、符号表、联合查找等
好处:
- 客户端有很多实现可供选择。
- 实现不需要知道客户端需求的细节。
- 许多客户端可以重用相同的实现。
- 设计:创建模块化的、可重用的库。
- 性能:在重要的地方使用优化的实现。
栈
API

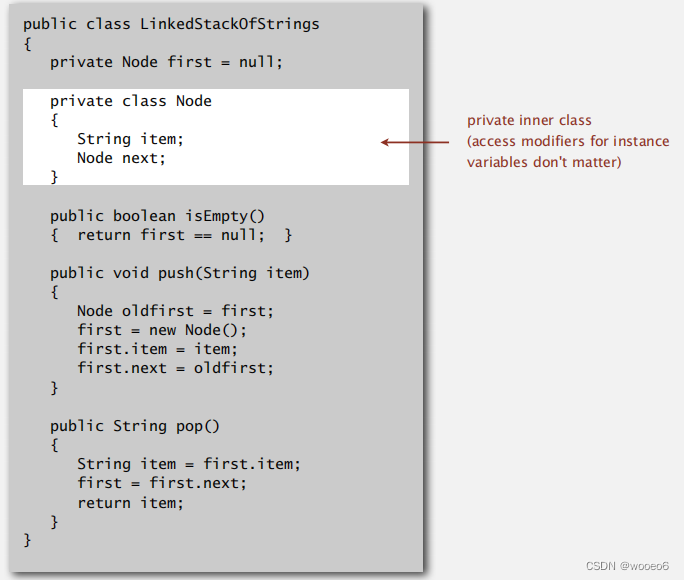
链表实现
节点定义

在链表头部增加/删除,实现Push/Pop

代码实现
性能:常数级别
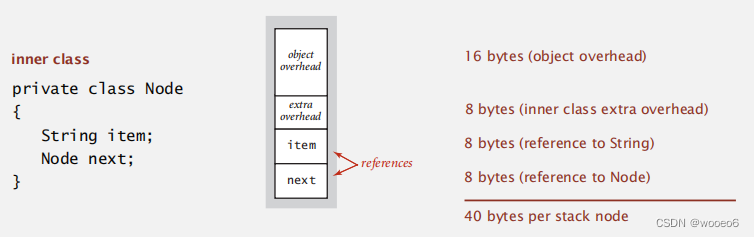
内存:有N个项的堆栈需要使用~ 40 N字节
节点对象开销16字节,8字节内部类的额外开销,8字节实际数据开销,8字节节点指针开销,共40字节
数组实现
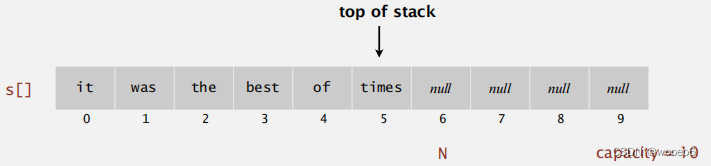
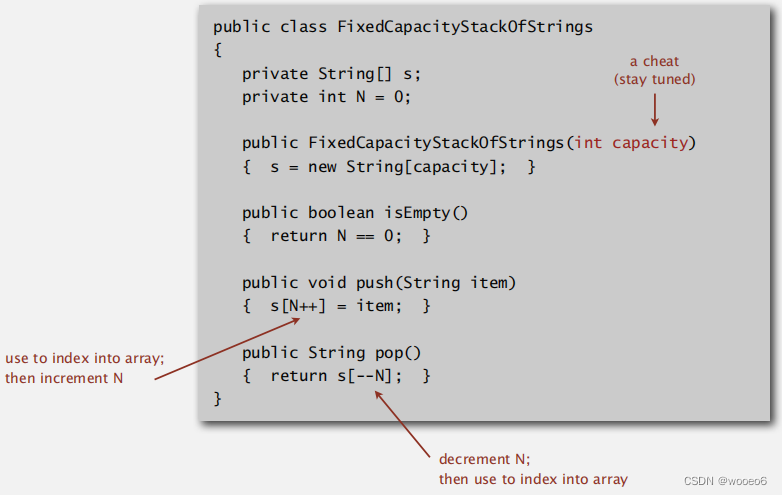
固定容量的数组实现栈
使用数组s[]可以在堆栈上存储N个项。
push():在s[N]处添加新项目。
pop():从s中删除项目
代码实现,需要客户端提供容量。
下溢出:如果从空堆栈中弹出,则抛出异常。
上溢出:使用调整数组大小的方法进行数组实现。后续改进。
允许插入null项。
游离:当不再需要时仍然保持对对象的引用。
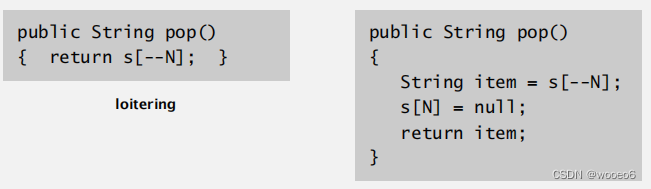
避免游离:将弹出的项手动设为null,只有在没有未完成的引用时,垃圾收集器才能回收对象的内存。
调整数组容量的实现
重复加倍:为了确保调整数组大小很少发生,如果数组已满,则创建一个两倍大小的新数组,并复制项目。

四分之一缩小:如果数组在满一半时缩小,可能存在抖动的情况,在一半的边界频繁增减,性能很坏。通用策略为当数组满四分之一时,数组缩小为数组的一半大小。

所以数组在25%到100%之间为满,此时数组要伸缩。
性能:因为数组的伸缩只发生在少数时间,平摊到整体中,也是常数级别。
内存:在8N到32N之间,在数组使用100%时8N,在数组使用25%时32N。
数组实现和链表实现比较
客户端可以使用由动态数组或链表实现的栈。哪一个更好?
链表实现即使在最坏的情况下,每次操作都需要恒定的时间。需要使用额外的时间和空间。
数组实现总的平均操作效率不错,平均时间比链表要少,浪费更少的空间。
结论:因为数组的单次操作时间不稳定,在伸缩数组时会慢,而链表每次都是常数时间是有保障的,所以对每次操作的时间都要求低且稳定的情况下应选择链表实现。比
如一架飞机进场等待降落,不想系统突然不能高效运转,或者互联网的路由器,数据包高速涌来,不想因为某个操作突然变得很慢而丢失一些数据,选择链表实现。如果关心总的时间,选择数组实现。
队列
API

链表实现
保存一个指针,指向单链列表中的第一个节点。
保存一个指针,指向单链列表中的最后一个节点。
从第一个队列开始退出队列。
从最后一个入队。
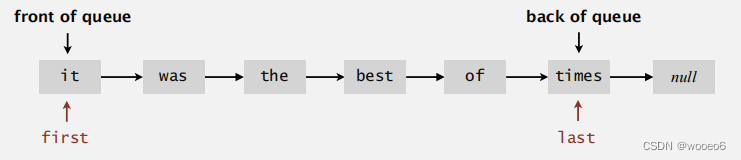
入队和出队
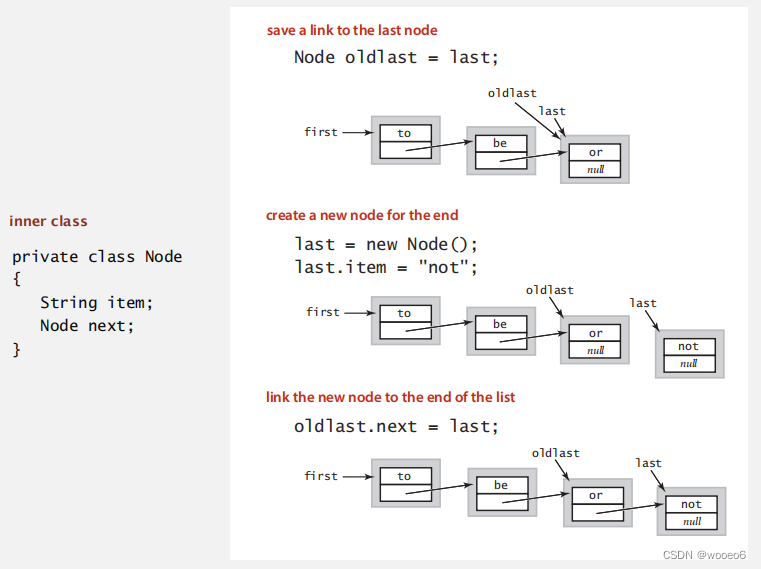
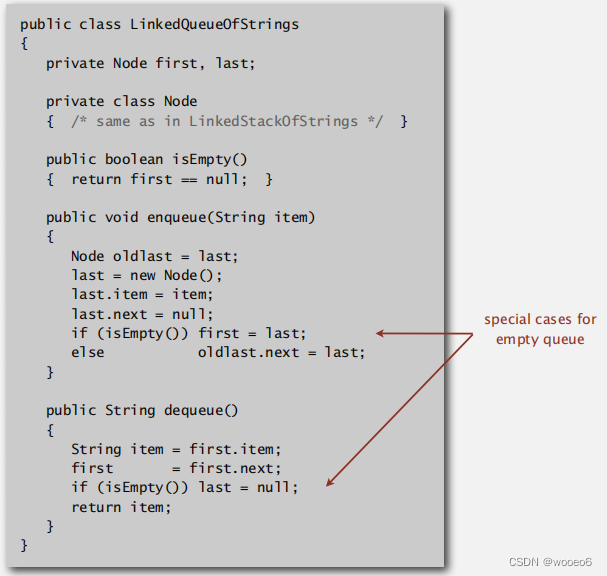
代码实现
数组实现
使用数组q[]存储队列中的项目。
enqueue():在q[]处添加新项目。
dequeue():从q[]头中删除项目。
更新头部和尾部的容量。
添加可调整的数组的大小。
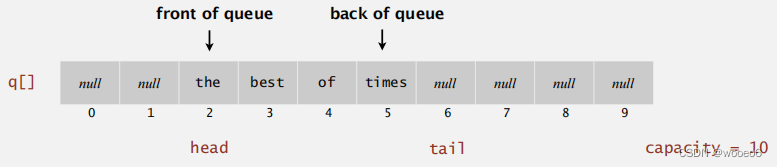
这个队列的实现并不完善,比如数组大小固定,当头部和尾部突破界限时未处理,后面自己完善。
泛型
因为要为栈和队列设计单独的接口和实现,如果为每种类型实现一个单独的堆栈类。重写代码非常乏味且容易出错。维护剪切粘贴代码是乏味且容易出错的。
链表实现
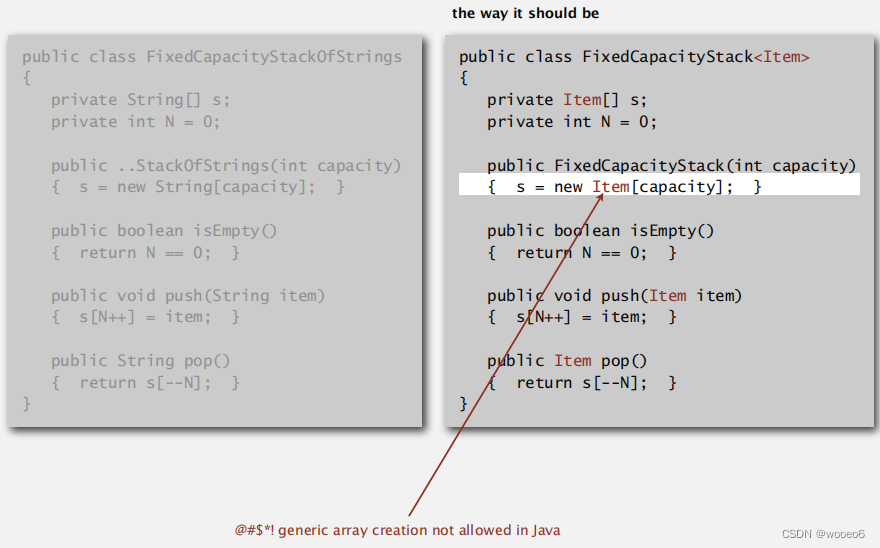
数组实现
java数组不支持泛型,所以不得不加入强制类型转换,强制类型转换因为编译时无法判断对错,会在运行时留下隐患,但是我们下面的代码是可靠的。

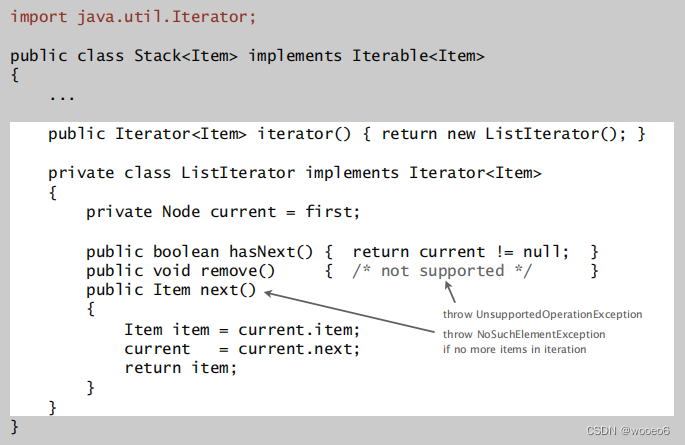
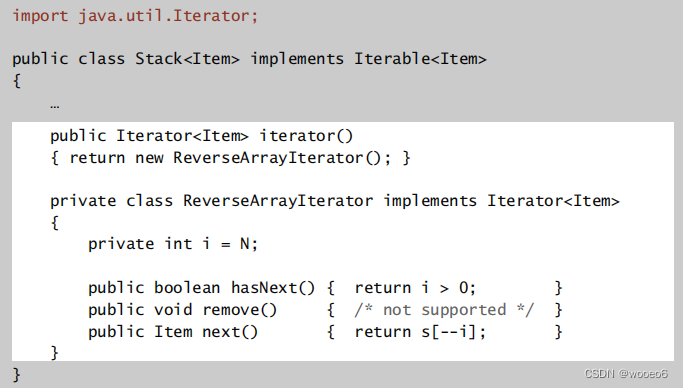
迭代器
目的:支持通过客户端对堆栈项进行迭代,而不透露堆栈的内部表示。实现foreach
什么是迭代器? 有方法hasnext()和next()
迭代器和非迭代器代码调用比较

利用java接口:
实现 Iterable<>接口
应用
栈的应用
- 在编译器中进行解析。
- Java虚拟机。
- 在文字处理器中进行撤销。
- Web浏览器中的后退按钮。
- 打印机的PostScript语言。
- 在编译器中实现函数调用。
另外:我们设计的栈或队列等在java库中有同样的功能的通用api,实现也是使用的可变大小数组,我们考虑的通用api也同样考虑了,但是有时候不直接使用那些api,因为公共库开发组设计的加入了越来越多的操作,api变、的过宽和臃肿,在api中拥有非常多的操作并不好,真正的问题在于关于库代码的性能知之甚少或者不能对其性能很好的估计,可能会因此遇到性能瓶颈。
比如我们需要访问一个序列的索引,如果我们自定义数组访问会是常数时间,但是如果用库的LinkedList帮助我们存储数据并访问索引则需要线性时间,这就隐藏的降低了我们的性能。
递归就是使用栈,实际上总是能显式的使用栈将递归程序非递归化,需要确定跳出递归的条件。
最大公约数
这是一个递归方式求最大公约数gcd()方法,p与q的最大公约数就是q与p mod q的最大公约数,如此反复对两个数取模求得。

Dijkstra双栈算术表达式
计算中缀算术表达式
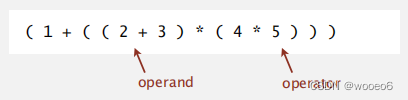
- 数值:推到数值栈上。
- 操作符:推入操作符栈上。
- 左括号:忽略。
- 右括号:出栈操作符和两个数值,并将运算结果入栈。
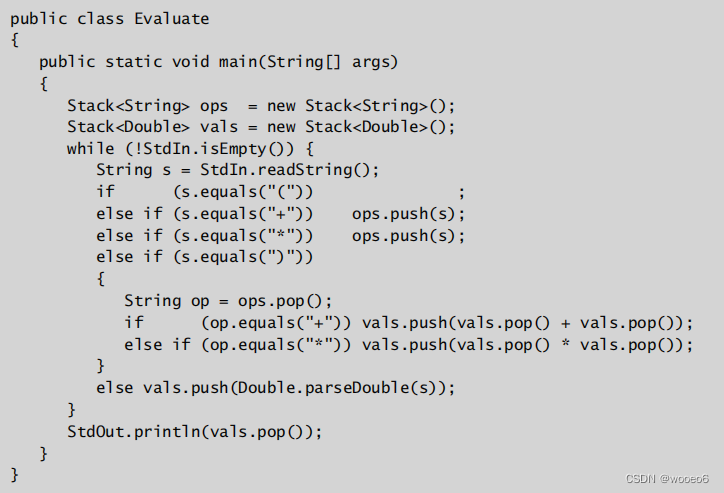
也就是当算法遇到一个在括号内被两个值包围的操作符时,它会先计算这两个值结果并将结果留在值栈上。

实际还可以扩展为更复杂,如更多的操作,优先顺序,结合性。
基本排序
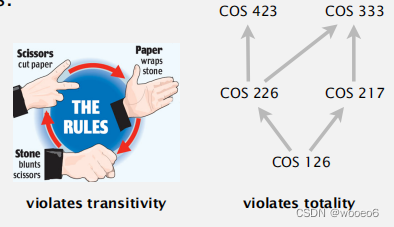
对任何类型的数据进行排序,总是一个二元关系,需满足:
- 对称性:如果v≤w和w≤v,那么v = w.
- 传递性:如果v≤w和w≤x,那么v≤x。
- 整体:v≤w或w≤v或两者都有
无传递性不行,如石头剪刀布。
无整体性不行。PU课程先决条件。
回调
因为我们的api要对任何类型的数据进行排序,也可能是自定义的类型,那么sort()如何知道不同类型的数据间的不同比较规则?
回调:引用可执行代码。客户端传递数组对象给sort()函数,sort()函数根据被调用对象的compareTo()方法进行比较。
不同语言实现回调的方式:
- Java:interfaces
- C:函数指针
- C++:class-type functors
- C#:delegates
- Python, Perl, ML, Javascript:first-class functions
如,对String类型的对象排序
String内部实现compareTo()方法,返回-1表示小于,1表示大于,0表示等于。

实现Comparable<>接口
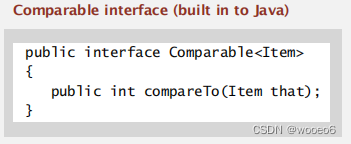
sort()实现中,比较对象大小,调用对象类型内部compareTo()方法

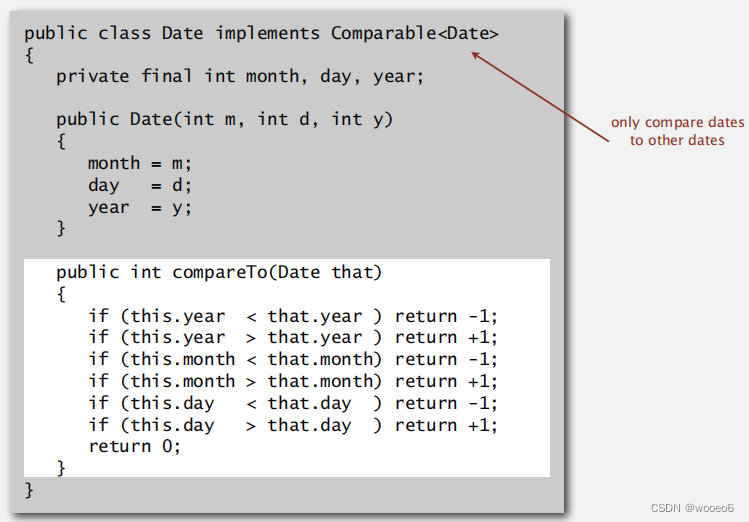
如自定义Date类型实现compareTo()方法
选择排序
归并排序
两种经典的排序算法:合并排序和快速排序
世界计算基础设施中的关键组件。对它们特性的充分科学理解使我们能够将它们发展成实际的系统分类。快速排序被评为20世纪科学和工程领域的十大算法之一。
归并排序
核心思想:将数组分成两半。递归排序的每一半。合并两部分。
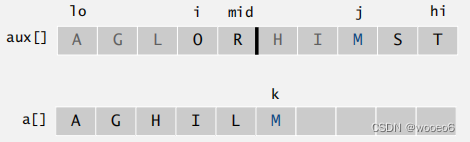
归并功能代码实现

MergeSort()代码实现
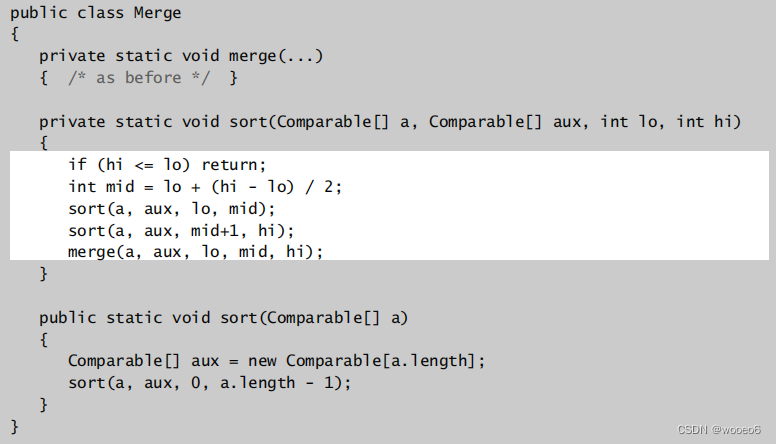
递归一分为二
归并过程
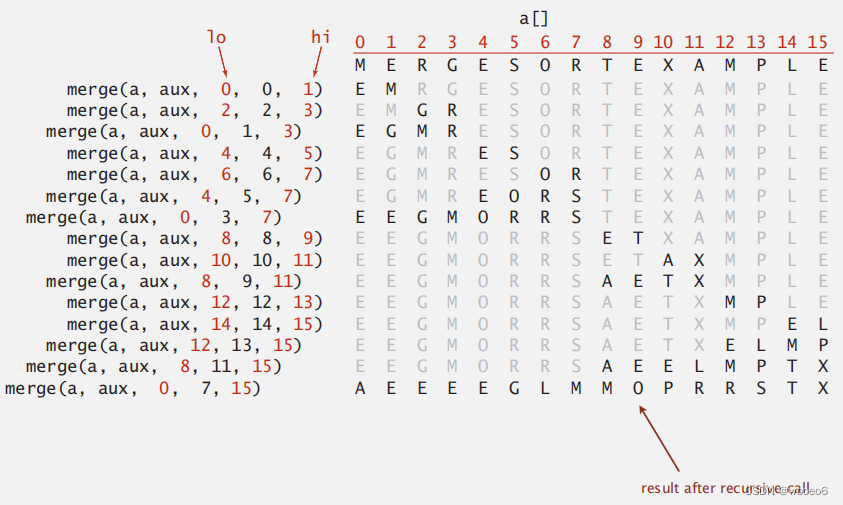
性能分析
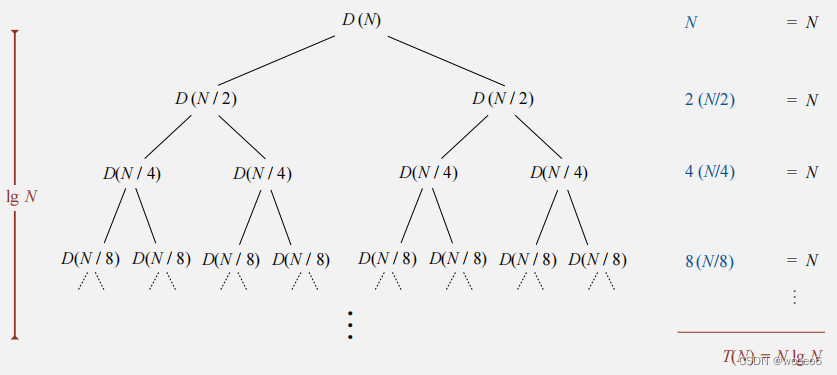
归并排序效率≤N lg N。需要一个长度为N的辅助数组
性能模型
假设N是2的幂次, 每一层合并N次,一共lg N层,共计N lg N
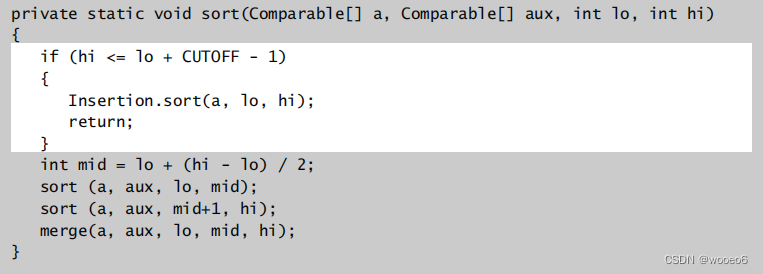
改进1:小数组使用插入排序
归并排序对于很小的子数组来说有太多的开销,比如函数调用与合并。所以对小的子数组使用插入排序,截止到≈10项时使用插入排序。
归并到最小数组长度为10
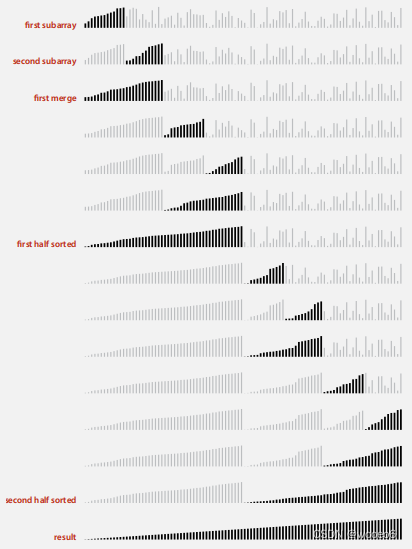
改进2:如果已经排序,停止合并
在合并前,如果前一半的数组已经比后一半的数组小,已经是最终的顺序,不再合并。
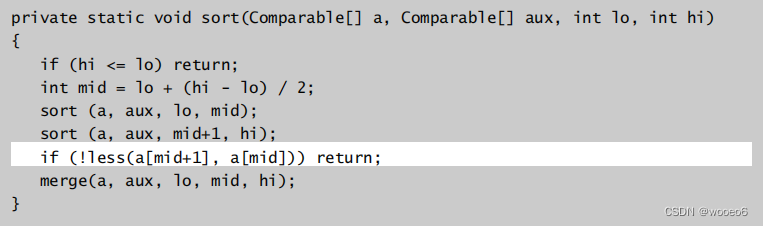
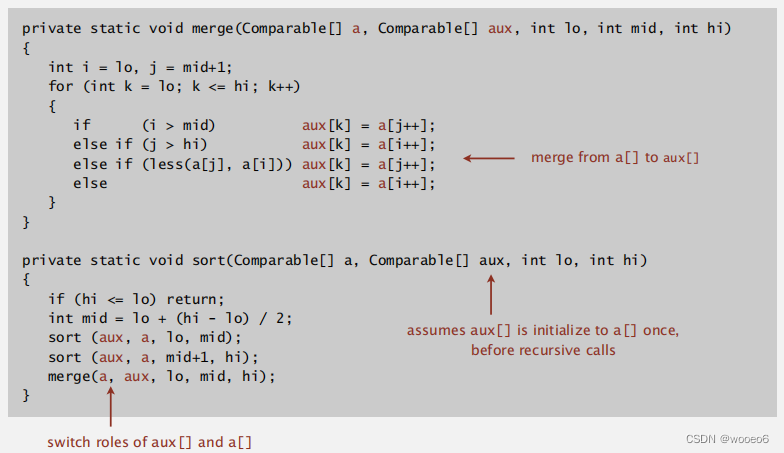
改进3:节省拷贝到辅助数组的时间
转换一下原数组和辅助数组的角色,不过还是需要辅助数组,可以节省时间,但不节省空间。