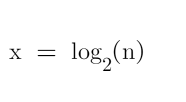目录

1 悬架系统

1.1 悬架结构示意图

1.2 悬架数学模型 

1.3 路面激励

2.仿真分析

2.1simulink模型

2.2 仿真结果

2.3 结论

3. 总结

---

1 悬架系统

1.1 悬架结构示意图

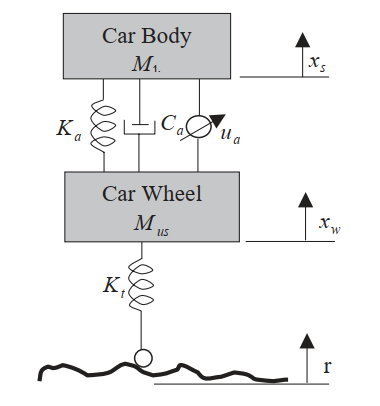
1.2 悬架数学模型 

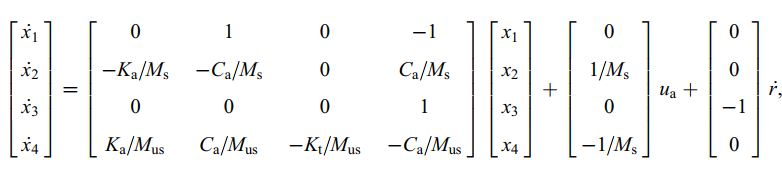
 其中：x1为悬架动扰度，x2为车身加速度，x3为轮胎动变形，x4为轮跳速度。

注：可以看到这样定义的悬架其路面扰度为速度，而非位移，这适用于我们在考察速度对悬架的影响。

1.3 路面激励

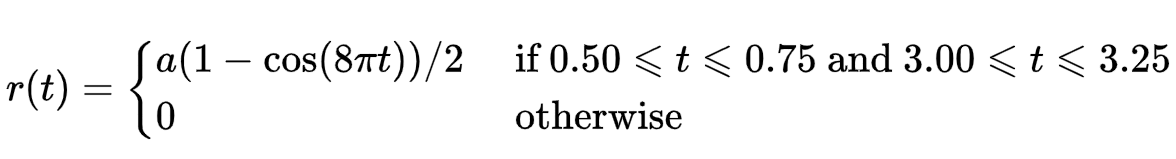
2.仿真分析

2.1simulink模型

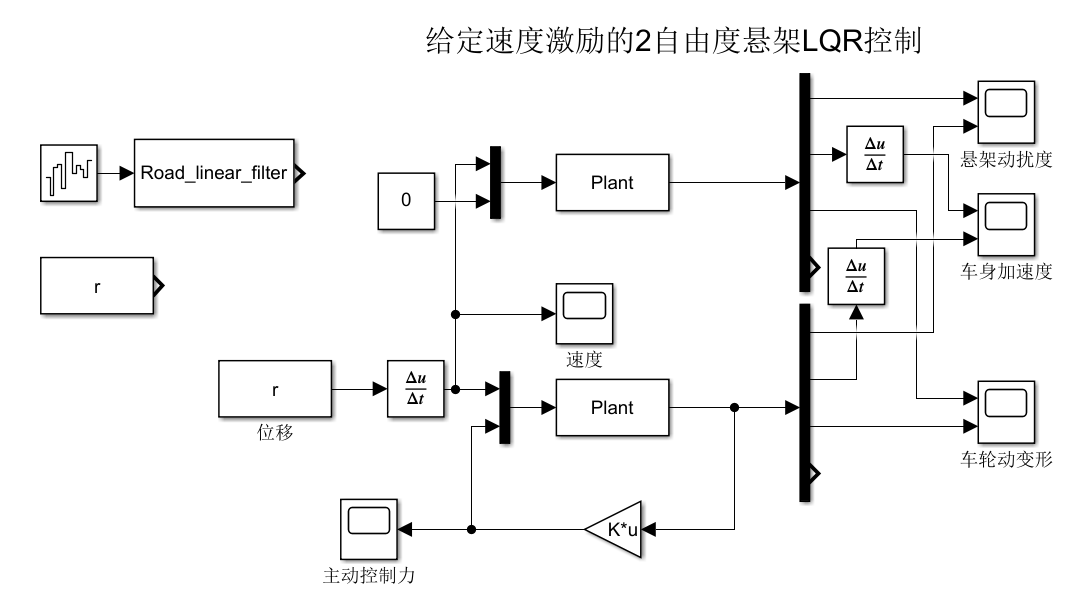
2.2 仿真结果

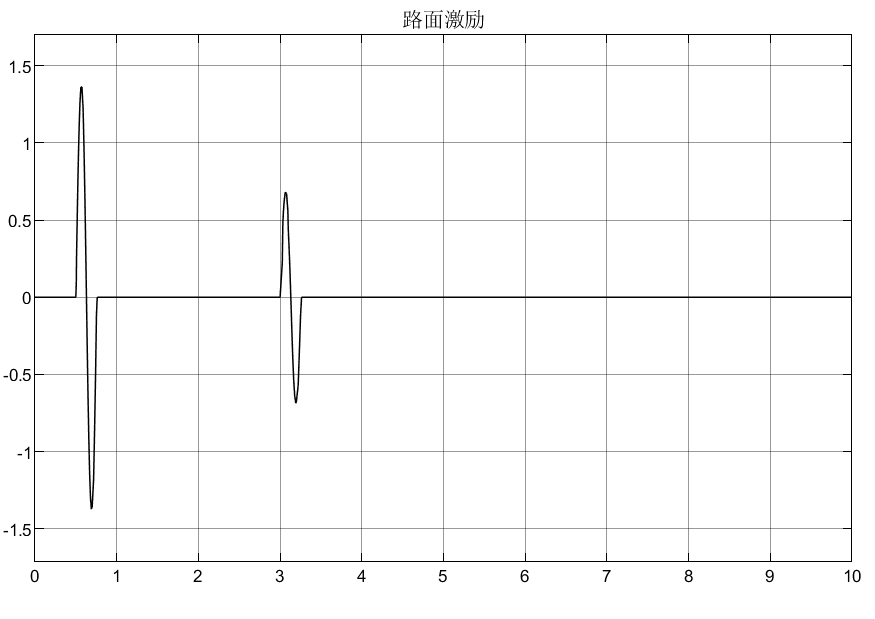
图1 路面激励 

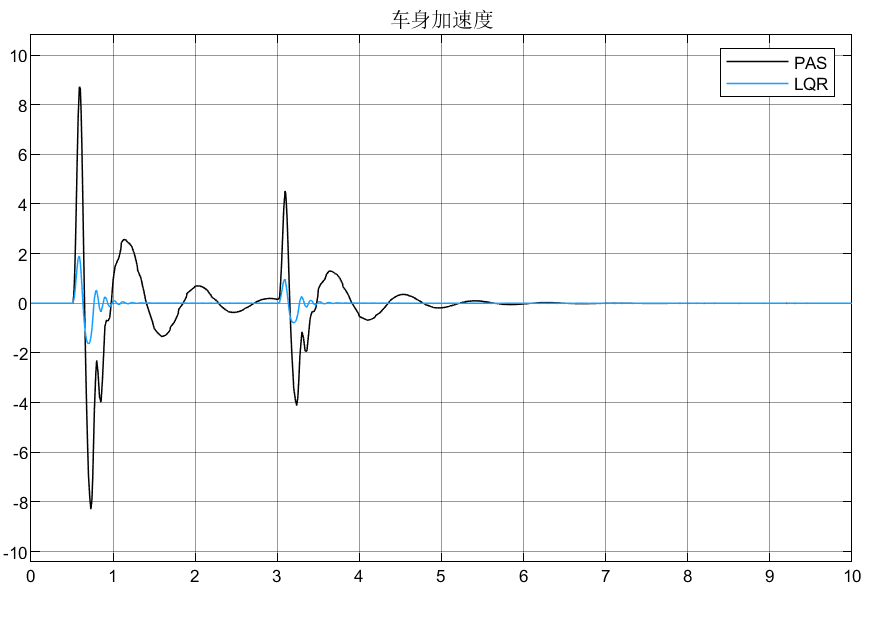
图2 车身加速度 

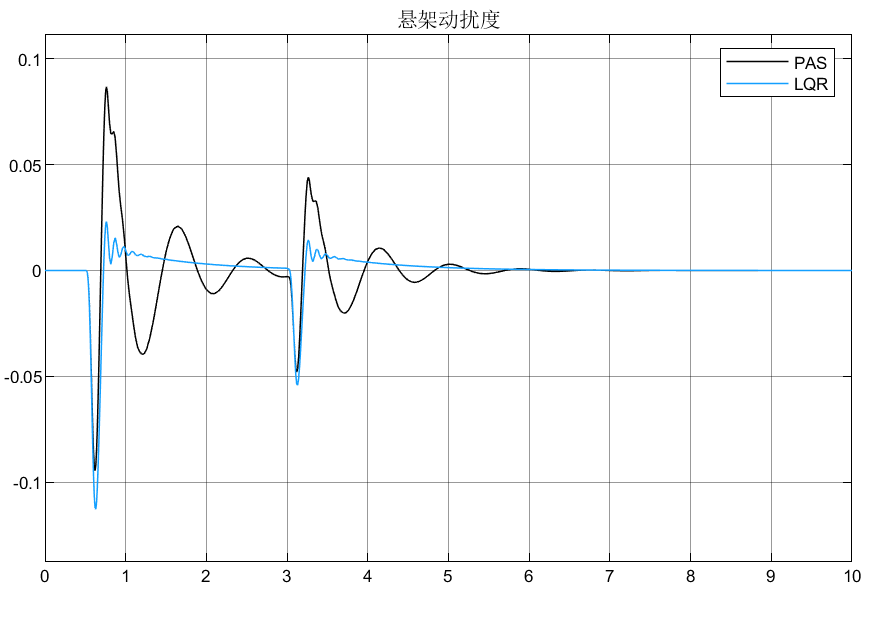
图3 悬架动扰度 

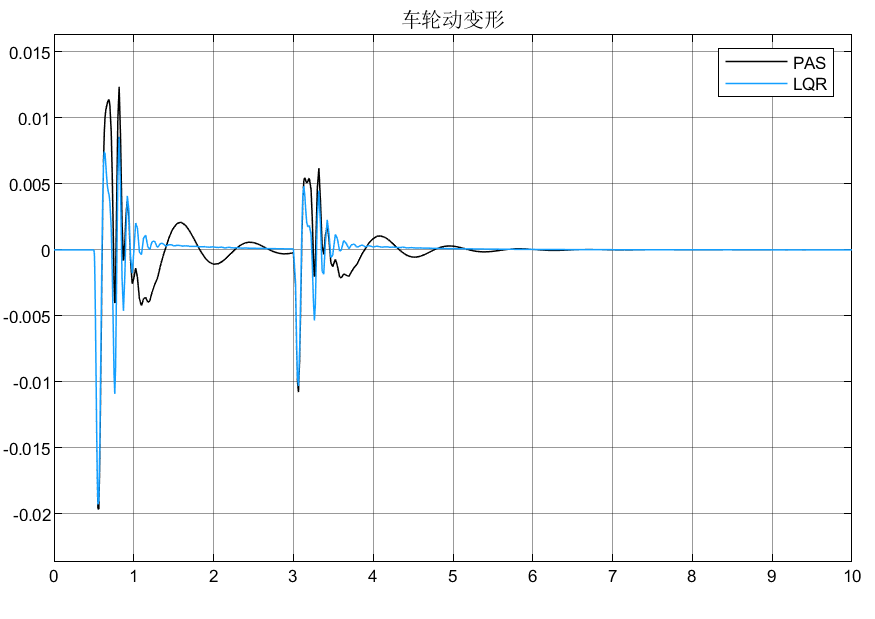
图4 车轮动变形 

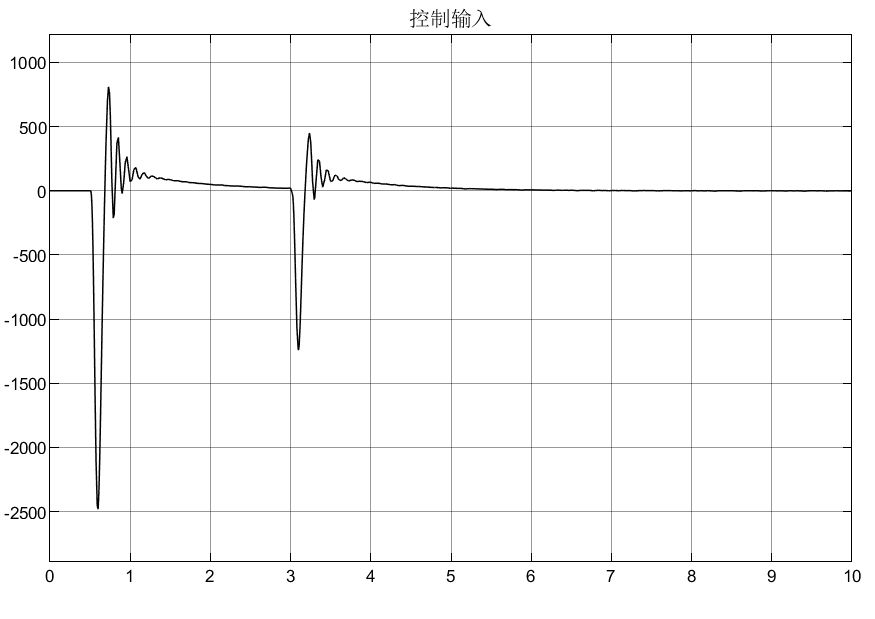
图5 控制输入 

2.3 结论

从图2可以看到，基于LQR的悬架控制很大程度的提高了乘坐舒适性，并且从图3和图4可以看到，改善车身加速度是基于车轮东变形和悬架动行程不被恶化的基础上改善的，说明了LQR对于悬架上的应用有较好的性能！

3. 总结

为什么对于悬架类的LQR控制常常将状态变量选择为车身速度、悬架动扰度、车轮动变形和轮跳速度这样的一种形式？

答：这是因为车身速度、悬架动扰度和车轮动变形是衡量悬架系统的控制好坏标准，而且输出性能指标也与其直接相关，所以在选择权重的时候可以根据所需的性能指标进行调节。