一个数组,1,2,3,4,5,...n; 一共n个数字。
1、直接查找
想要查询第n个数字,直接搜索,就是n次查询。
ps:那么问题来了,这样查询也太慢了,有什么改进的呢?
2、二分查找
这个时候,二分查找更快。不过就是得先把数组排好序。
乱序,二分就没有用处了。
想要查询第n个数字,二分查找,2的x次方 = n;
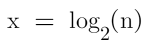
ps:问题也就出来了。每次都需要排好序。这样也太麻烦了,每次都要去做个排序,冒泡啥的,他们插入删除操作,移动元素又多,有什么比较好的解决办法吗?
3、二叉查找树(又名二叉排序树,二叉搜索树)
变成树结构
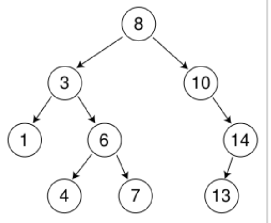
这样,查询也是和二分查找的速度差不多。
次数。其实是h 也就是高度。
h层,有2(h-1)的元素,第1层,2^(0) = 1,一共h层。那么总的数量是 N,按照二叉树排列。
S=1+2+4+8+2^(h-1) = N
按照等比数列求和的公式
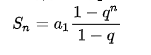

2^h-1=n
那么高度h就是相当于,
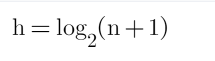
相当于二分查找。
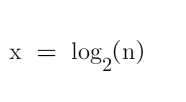
但是这个二叉树,查询快是快,但是增加,删除,修改都会带来巨大的元素移动消耗,且很难保持高效率的查询。
那么将会发生怎么样的变化?
4、AVL数(二叉平衡树) AVL,艾薇儿树。
AVL树是最早发明的自平衡二叉搜索树之一AVL 取名于两位发明者的名字G. M. Adelson-Velsky 和 E. M. Landis(来自苏联的科学家)Something interesting有人把AVL树念做“艾薇儿树”加拿大女歌手,几首不错的歌:《Complicated》、《When You're Gone》、《Innocence》
https://www.jianshu.com/p/9abaa8155ffc
每次新增,修改,删除。都会去计算每个节点的平衡因子。
也就是
| hight(左子树)-hight(右子树) | <=1
每个节点重新去算平衡。通过按住你插入的关键节点,左旋右旋的方法,调整成AVL树。
右旋,右边的旋转。往上提
左旋,左边的旋转。往上提。
LL-> R右旋。
RR->L左旋
LR - >看成 LL(RR),先RR左旋,变成LL,再右旋
RL ->看成 RR(LL),先LL右旋,变成RR,再左旋
1. 添加
可能会导致都失衡
只要让高度最低的失衡节点恢复平衡,整棵树就恢复平衡【仅需 O(1)次调整】
2. 删除
可能会导致或失衡(只有1个节点会失衡)
恢复平衡后,可能会导致更高层的祖先节点失衡【最多需要 O(logn)次调整】
3. 平均时间复杂度
搜索:O(log n)
添加:O(log n),仅需O(1)次的旋转操作
删除:O(log n),最多需要O(logn)次的旋转操作
计算机,默认底数为2.
底数一般是2 因为二分啊,快排啊,线段树啊之类的算法一般是以二分为思想的!
是的哦,AVL 因为是平衡树,所以树的高度最高是 logn 级别,各项操作也都是 logn 级别的:)
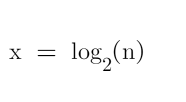
二叉平衡树。太讲究平衡了。增删改查,都是log n的级别, 如果对平衡架构没那么要求的。什么都要一般般快。