电子技术——内部电容效应以及MOS与BJT的高频响应模型

耦合和旁路电容决定了放大器的低频响应，同时内部电容效应决定了放大器的高频响应。本节，我们简单简单介绍一下内部电容效应，并且更重要的是如何在小信号模型中模型化内部电容效应。

MOSFET

在我们之前学习MOSFET的时候，我们就已经知道MOS中存在内部电容。实际上，我们已经在使用栅极和沟道之间的内部电容，即场效应。之前，我们假设MOS中的电容都是稳态的，也就是我们忽略了电容的充电和放电时间。结果就是我们并没有考虑电容的任何频率效应。实际上，MOSFET放大器在高频的时候增益会有所减小。同样的，在之后数字电路的章节，我们会学习MOS数字逻辑反相器会显示出有限的传播延迟。为了考虑这些情况，我们必须把内部电容考虑进去。这就是本节我们要讨论的。

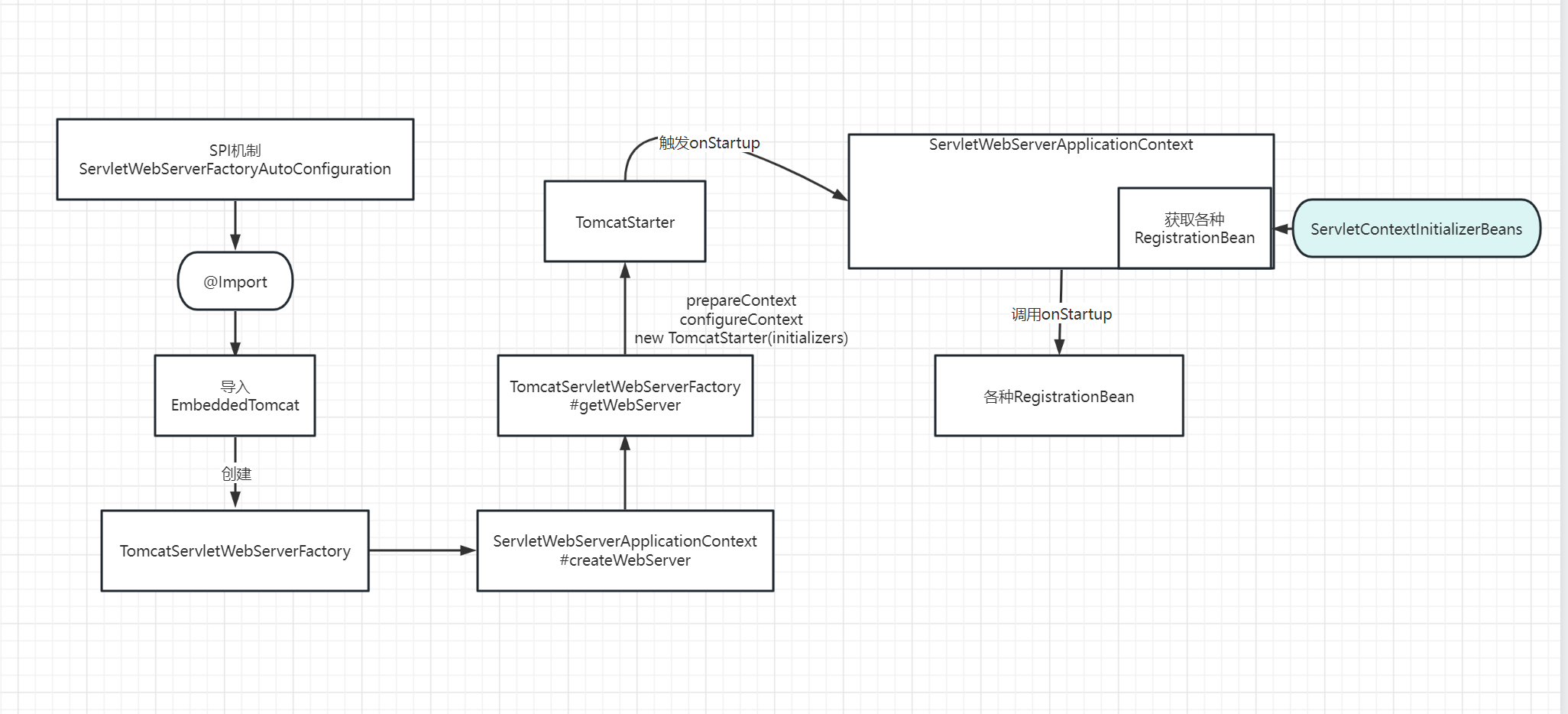
为了说明产生内部电容的物理原因，我们使用下面的图片：

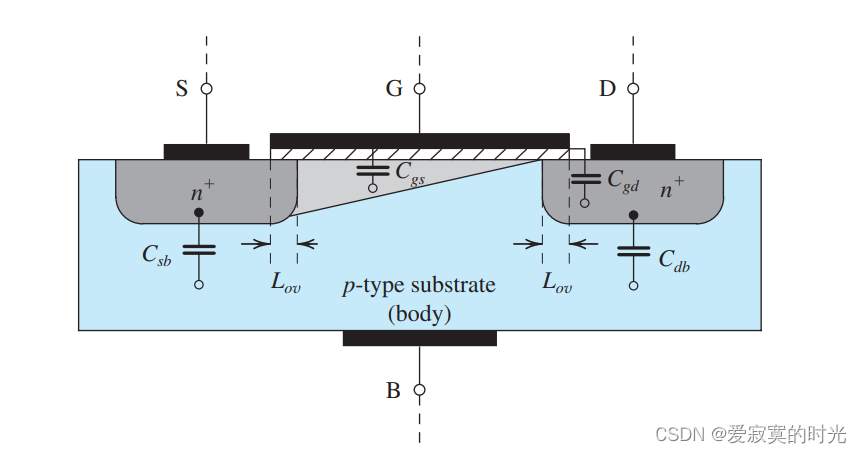
上图是一个N沟道的MOSFET，并且处于饱和区。如图，存在四个电容。其中两个 $C_{gs}$ 和 $C_{gd}$ 通过栅极电容效应形成，另外两个 $C_{sb}$ 和 $C_{db}$ 是pn结的耗散区电容。

之前我们介绍过栅极电容，其中的硅氧化物层充当电介质，金属极板和沟道形成一个平行板电容器，每单位面积的容值记为 $C_{ox}$ 。当MOS处于饱和区的时候，我们知道总容值是 $\frac{2}{3}WL{C}_{ox}$ 。除此之外，因为极板与源极区和栅极区分别有一个小的重叠面积，重叠长度为 $L_{ov}$ ，则重叠部分的电容为：

$$C_{ov}=W{L}_{ov}{C}_{ox}$$

一般的， $L_{ov}=0.05L\sim 0.1L$ 。现在我们能表示出栅极到源极直接的电容为：

$$C_{gs}=\frac{2}{3}WL{C}_{ox}+C_{ov}$$

对于栅极到漏极之间的电容，我们注意到沟道被截断，所以电容只由重叠部分组成：

$$C_{gd}=C_{ov}$$

对于耗散层的电容，可以使用我们之前推导的反向偏置pn结中的电容表达式：

$$C_{sb}=\frac{C_{sb0}}{\sqrt{1+\frac{V_{SB}}{V_0}}}$$

其中 $C_{sb0}$ 是在体极和源极之间无偏置时候的电容值， $V_{SB}$ 是反向偏置电压的大小， $V_0$ 是pn结内建电压（0.6V 到 0.8V），同样的对于体极和漏极之间的电容：

$$C_{db}=\frac{C_{db0}}{\sqrt{1+\frac{V_{DB}}{V_0}}}$$

我们发现，对于两个电容的过度系数均为 $m=1/2$ 。

值得注意的是，每一个结电容都是由耗散区的底部和周围的三个面（第四个面向沟道）分别贡献而成。上述表达式都是建立在小信号模型的表达式上。

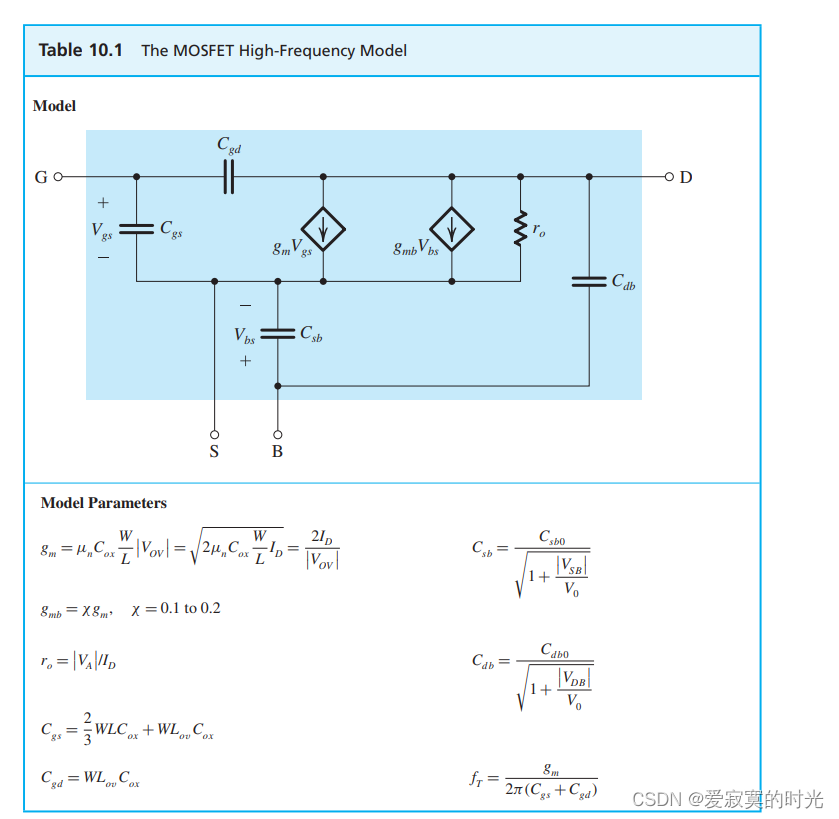
MOSFET的高频模型

下图展示了MOSFET的高频模型，其中包括我们介绍的四个电容：

这个模型可以用来计算MOS放大器的高频响应，然而这个模型实在是太复杂了，不管是对于手动分析还是计算机仿真分析来说。幸运的是，如果体极和源极是相连的，我们的模型可以大大简化：

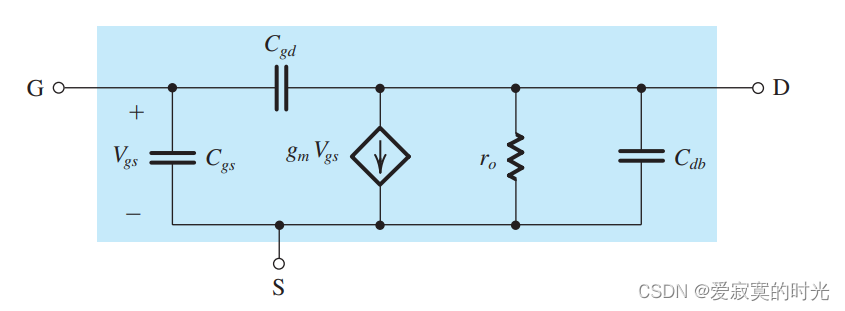
在这个模型中， $C_{gd}$ 尽管很小，但是对于决定高频响应有至关重要的作用，不能忽略。但是电容 $C_{db}$ 在高频响应分析中基本可以忽略，忽略之后的模型如下：

最后对应的T模型为：

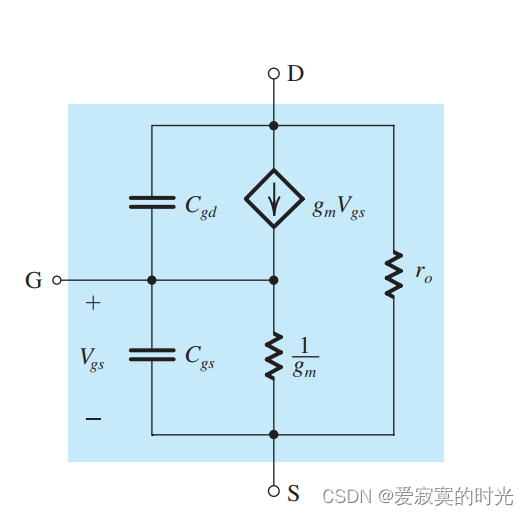
MOS的单位增益频率

对于MOS放大器来说，有一个重要的参数就是单位增益频率 $f_T$ ，也称为 过度频率 。定义为CS放大器配置时的短路电流是单位电流增益时候的频率。下图展示了一个CS放大器的混合 $\pi$ 模型。为了决定短路电流增益，我们在输入端放入测试电流源 $I_i$ ，并且短路输出端：

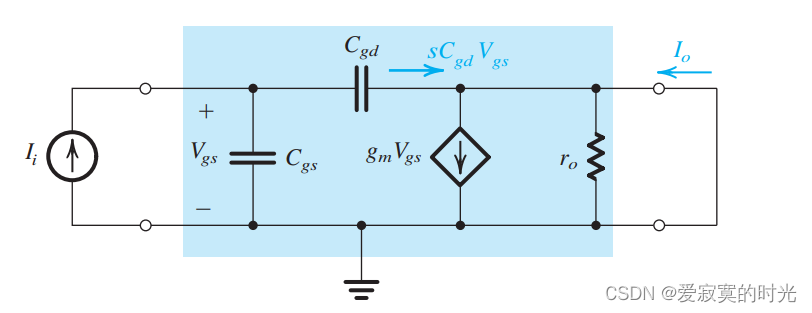
通过简单的计算得出，输出电流为：

$$I_o=g_m{V}_{gs}-s{C}_{gd}{V}_{gs}$$

回想一下 $C_{gd}$ 非常小，我们可以忽略第二项：

$$I_o\simeq g_m{V}_{gs}$$

我们可以导出 $V_{gs}$ ：

$$V_{gs}=\frac{I_i}{s(C_{gs}+C_{gd})}$$

则电流比为：

$$\frac{I_o}{I_i}=\frac{g_m}{s(C_{gs}+C_{gd})}$$

带入物理频率 $s=j\omega$ 得到：

$$|\frac{I_o}{I_i}|=\frac{g_m}{\omega (C_{gs}+C_{gd})}$$

则单位增益时候的频率是在：

$${\omega }_T=g_m/(C_{gs}+C_{gd})$$

或是：

$$f_T=\frac{g_m}{2\pi (C_{gs}+C_{gd})}$$

因为 $f_T$ 正比于 $g_m$ ，并且 $g_m$ 决定了中频带的增益。反比与 $(C_{gs}+C_{gd})$ 限制了放大器的带宽， $f_T$ 的值越大，MOS的频率效率就越好。

一般的， $f_T$ 对于旧技术（5um COMS）来说在100MHz，对于高速新技术（0.13um COMS）在几GHz。

总结

BJT

与MOS同样的，BJT也存在内部电容效应。

基极充电或扩散电容 $C_{de}$

当BJT工作在主动模式下，次载流子充满基极区域。对于npn晶体管，基极区域充满了电子，我们记电荷量 $Q_n$ 可以表示为：

$$Q_n={\tau }_F{i}_C$$

其中 $i_C$ 是集电极电流， ${\tau }_F$ 是器件的时间常数，具有时间量纲，被称为 前向基极-过渡时间 ，表示一个次载流子（电子）通过基极区域的平均时间。一般情况下，在 10ps 到 100ps。

上式是一个大信号模型，因为 $i_C$ 与 $v_{BE}$ 呈现指数关系，同时 $Q_n$ 也同样依赖于 $v_{BE}$ 。对于小信号模型，我们定义 小信号扩散电容 ：

$$C_{de}\equiv \frac{d{Q}_n}{d{v}_{BE}}={\tau }_F\frac{d{i}_C}{d{v}_{BE}}={\tau }_F{g}_m={\tau }_F\frac{I_C}{V_T}$$

这里 $I_C$ 是集电极偏置电流。因此当 $v_{be}$ 改变 $v_{BE}$ 的时候，发射极电流增加 $g_m{v}_{be}$ 因此电荷量增加 ${\tau }_F{g}_m{v}_{be}$ 多出来的电荷由基极电流提供。

基极-发射极结电容 $C_{je}$

在BJT的主动模式下，基极和发射极直接存在电容 $C_{je}$ ，我们知道，正向偏置的pn的电容为：

$$C_{je}\simeq 2C_{je0}$$

这里 $C_{je0}$ 是零偏置下的电容。

集电极-基极结电容 $C_{\mu }$

在在BJT的主动模式下，集电极-基极是一个反向偏置的pn结，我们称其为 耗散电容 ，其值为：

$$C_{\mu }=\frac{C_{\mu 0}}{(1+\frac{V_{CB}}{V_{0c}}{)}^m}$$

这里 $C_{\mu 0}$ 是无偏置下的电容。 $V_{CB}$ 是反向电压， $V_{0c}$ 是内建电压（0.75V）， $m$ 是过渡系数（0.2-0.5）。

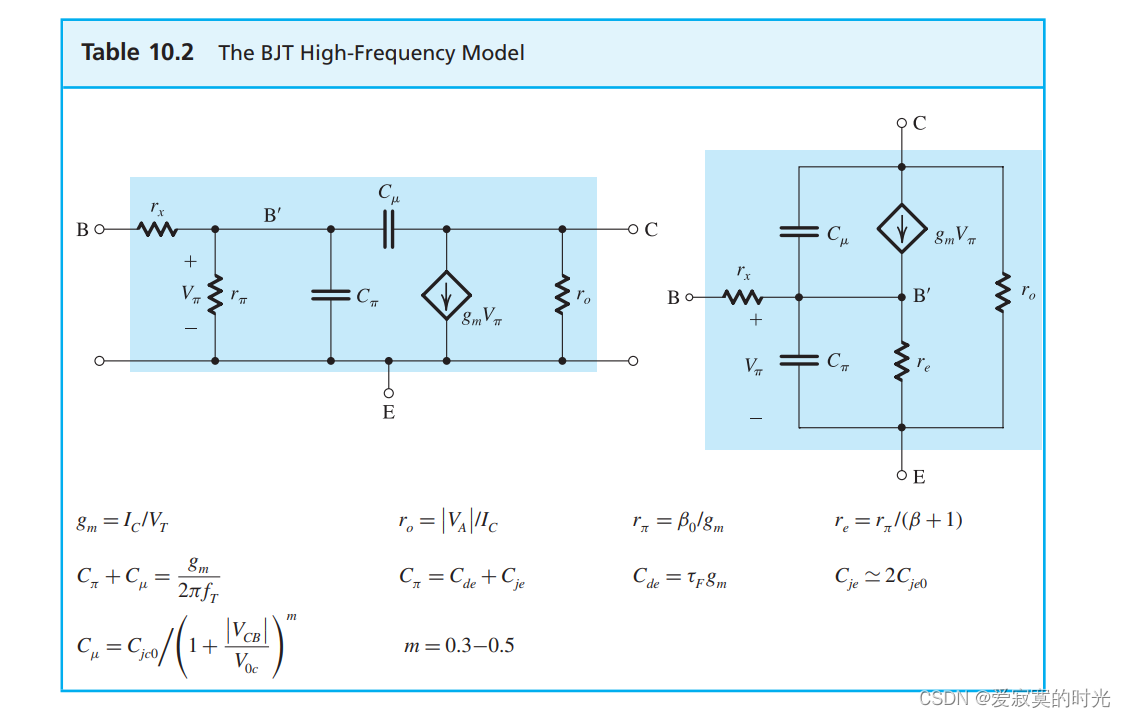
高频模型

下图展示了BJT的混合 $\pi$ 和T模型下的高频模型。

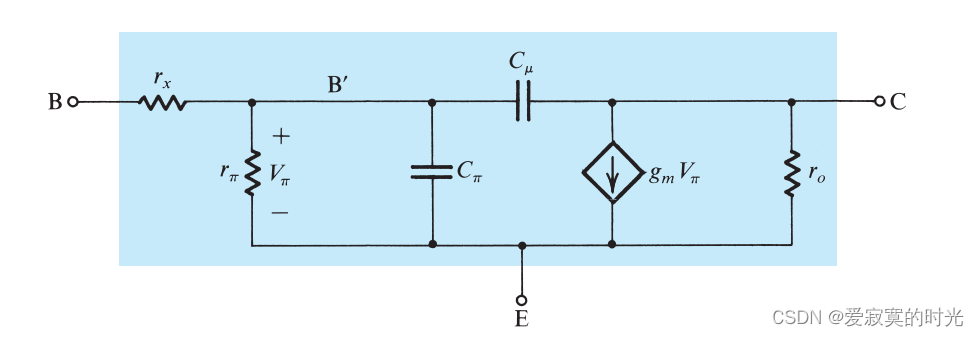
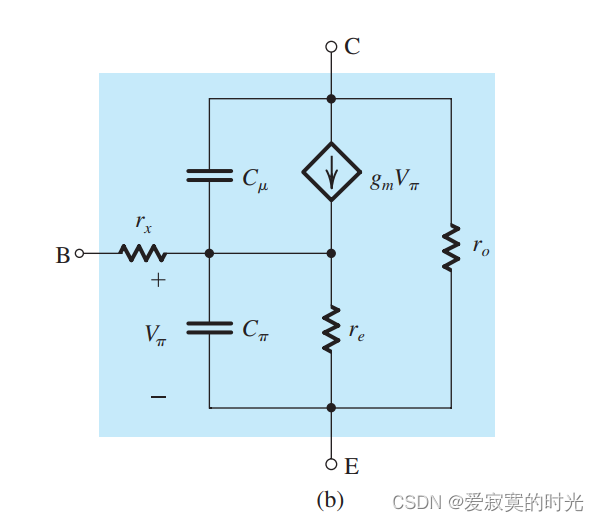
在图中，分别有两个电容，一个是发射极到基极的电容：

$$C_{\pi }=C_{de}+C_{je}$$

另一个是集电极到基极的电容 $C_{\mu }$ 。除此之外，我们还添加了基极的固有电阻 $r_x$ 在外部基极B和内部基极B‘之间，因为 $r_x\ll r_{\pi }$ 因此在低频模型下，我们可以忽略，但是在高频模型下，这个电阻是通过电流的并且和电容相互作用，就无法忽略。

BJT的单位增益频率

在datasheet中通常不直接给出 $C_{\pi }$ 而是给出 $\beta$ 与频率之间的关系。为了决定 $C_{\pi }$ 和 $C_{\mu }$ 我们需要导出与 $\beta$ 之间的关系。我们使用下面的CE短路电流：

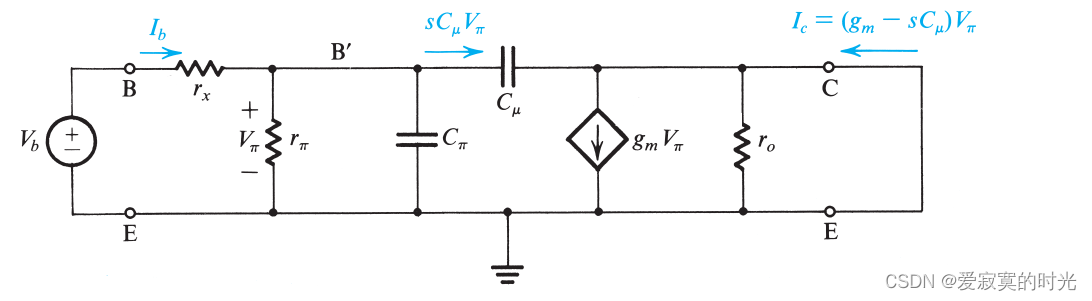
在节点C的电流为：

$$I_c=(g_m-s{C}_{\mu })V_{\pi }$$

这里 $V_{\pi }$ 和 $I_b$ 的关系为：

$$V_{\pi }=I_b(r_{\pi }||C_{\pi }||C_{\mu })$$

则电流比为：

$$h_{fe}=\frac{I_c}{I_b}=\frac{g_m-s{C}_{\mu }}{1/r_{\pi }+s(C_{\pi }+C_{\mu })}$$

在一定的频率下， $\omega C_{\mu }\ll g_m$ 因此：

$$h_{fe}\simeq \frac{g_m{r}_{\pi }}{1+s(C_{\pi }+C_{\mu })r_{\pi }}=\frac{{\beta }_0}{1+s(C_{\pi }+C_{\mu })r_{\pi }}$$

这里的 ${\beta }_0$ 为低频下的 $\beta$ 并且 $h_{fe}$ 存在一个单极点频率，此时为 $3dB$ 响应：

$${\omega }_{\beta }=\frac{1}{(C_{\pi }+C_{\mu })r_{\pi }}$$

下图展示了该电路的高频响应：

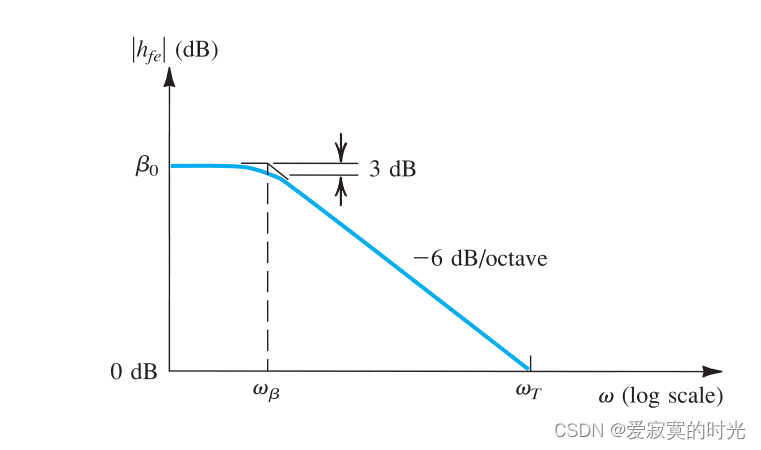
存在单位增益频率 ${\omega }_T$ ：

$${\omega }_T={\beta }_0{\omega }_{\beta }=\frac{g_m}{C_{\pi }+C_{\mu }}$$

$$f_T=\frac{g_m}{2\pi (C_{\pi }+C_{\mu })}$$

这个形式和MOS的一致。

通常在datasheet中给出 $f_T$ ，而 $f_T$ 是一个关于偏置电流的参数：

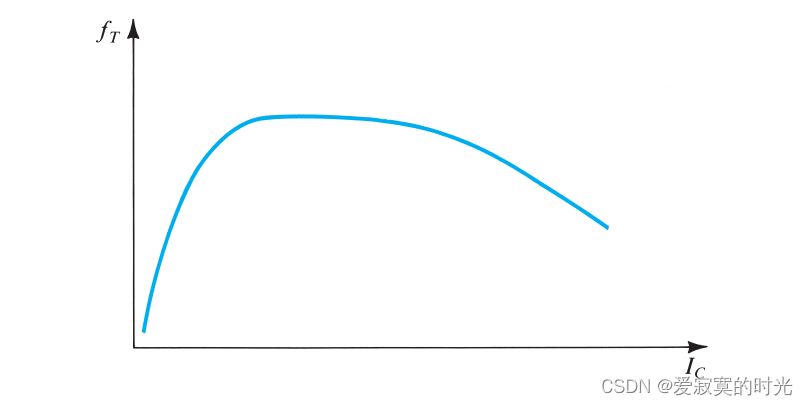
我们发现，在较低的偏置电流下，单位增益频率也较低。但是随着偏置电流继续加大，单位增益频率却降低了，此时不能使用上述表达式解释其原因，主要原因在 ${\beta }_0$ 在大电流的情况下会下降。在 $f_T$ 的常数区域，$C_{\pi }$ 主要由扩散部分组成且远大于 $C_{\mu }$ 因此 $C_{\pi }+C_{\mu }\simeq C_{de}={\tau }_F{g}_m$ ：

$$f_T=\frac{1}{2\pi {\tau }_F}$$

一般情况下，$f_T$ 在 100MHz到几十GHz。

关于高频模型，当频率处于 $5\sim 10f_{\beta }$ 的时候，我们可以忽略 $r_{\pi }$ 此时的阻抗由 $r_x$ 决定。因此在高频模型下 $r_x$ 具有关键作用。

在结束本节之前，我们应该注意到在高频模型下，BJT能够精准的工作直到 $0.2f_T$ 。若想获得更大的 $f_T$ 需要往BJT模型中加入更多的寄生元件。

总结