链接

题意：

给定一个 n 个点 n 条边的图 ，n 为 6 的倍数，每条边都有边权。

这个图是由 n/3 个三元环构成的 [1,2,3],[4,5,6],[7,8,9],[10,11,12]......

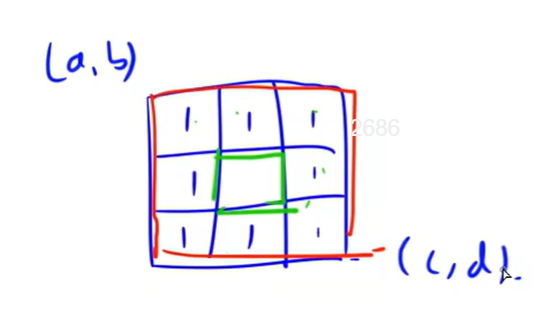
一个 n=12 的图长成这个（唯一）：

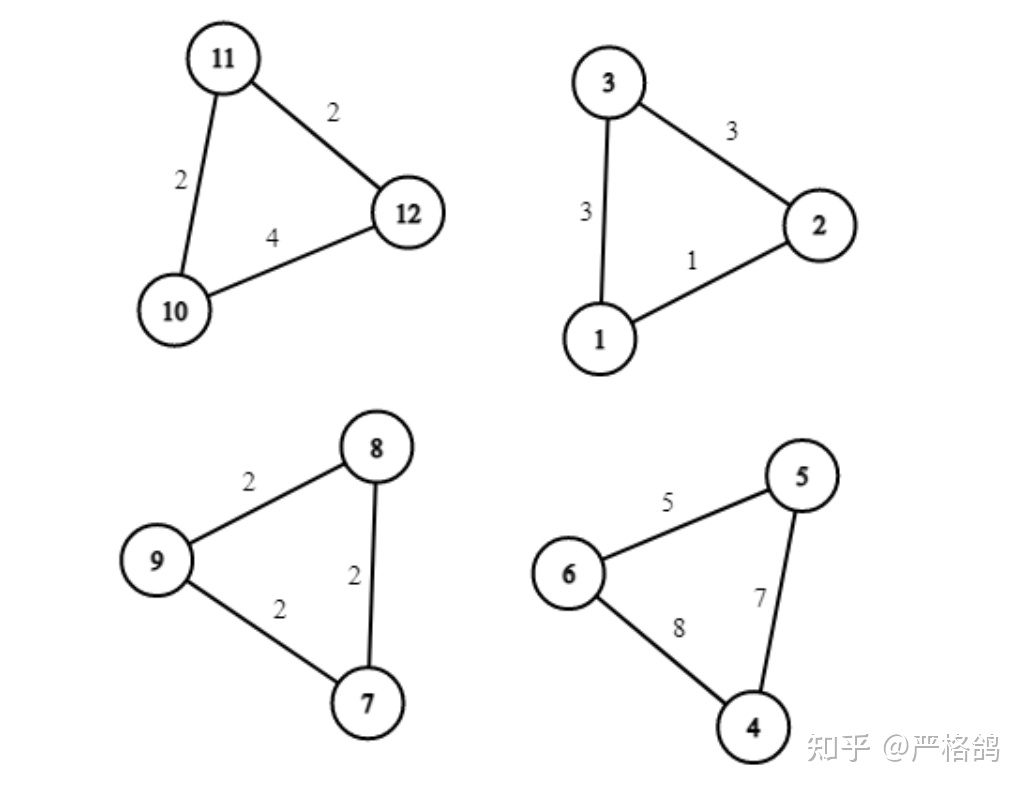
现在你需要给图染上红蓝两种颜色。每种颜色要刚好染色 n/2 个点。

定义染色的权值 W 为，两个端点的颜色不同的边，边权的总和。

例如下图 W=1+4=5

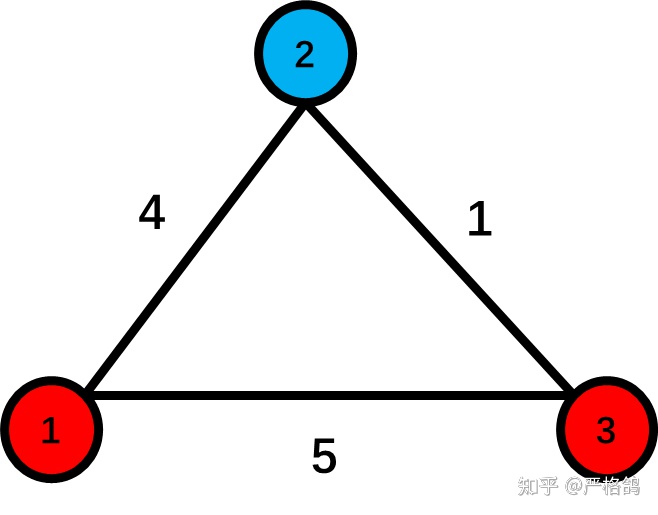
现在你需要找到染色方案使得 W 最大，输出，有多少种染色方案可以使得 W 最大。

做法：

首先，因为图的构成是多个三元环。所以可以独立的考虑每个三元环。

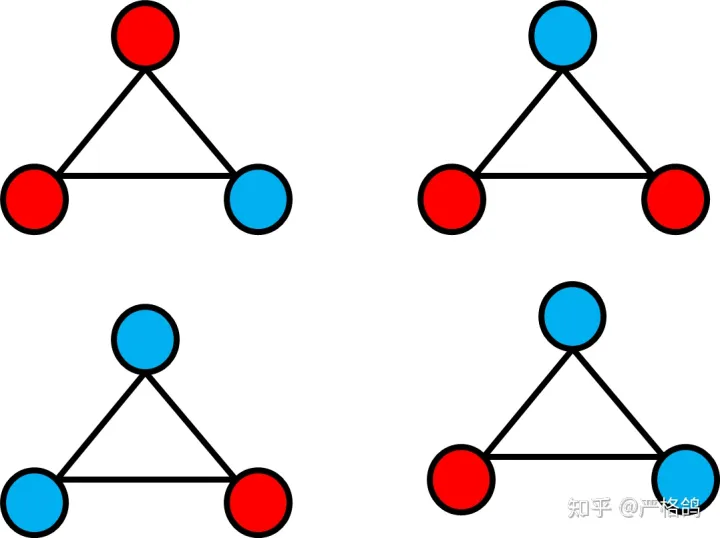
对于每个三元环来讲，我们最多可以通过染色，使其贡献出两条边。

也就是，我们用，两个颜色加另一个颜色就可以使得一个三元环贡献出两条边。

那么这两条边的边权要最大（方案可以直接枚举，下面看代码即可）

问题是，要求红色蓝色各种一半。

所以一定是，这 n/3 个三元环中，有一半是“两个蓝色一个红色”，另外一半是“两个红色一个蓝色”。

参考代码：

#include <bits/stdc++.h>

using ll = long long;
const int mod = 998244353;
//=====组合数板子===============
namespace CNM
{
    const int N = 3e5 + 5;
    ll quick(ll x, ll n) {
        ll res = 1;
        while (n) {
            if (n & 1)
                res = (res * x) % mod;
            x = x * x % mod;
            n >>= 1;
        }
        return res;
    }
    ll inv(ll x) { return quick(x, mod - 2); }
    ll fac[N], invfac[N];
    void init() {
        fac[0] = 1;
        for (int i = 1; i < N; ++i)
            fac[i] = (fac[i - 1] * i) % mod;
        invfac[N - 1] = inv(fac[N - 1]);
        for (int i = N - 2; i >= 0; --i)
            invfac[i] = (invfac[i + 1] * (i + 1)) % mod;
    }
    ll C(int n, int m) {
        if (n < m || m < 0)
            return 0;
        return fac[n] * invfac[m] % mod * invfac[n - m] % mod;
    }
}
//=====组合数板子===============
void solve() {
    int n;
    std::cin >> n;
    ll ans = 1;
    for (int i = 1; i <= n; i += 3) {
        int w1, w2, w3;
        std::cin >> w1 >> w2 >> w3;
        std::vector<int> e = {w1, w2, w3};
        int mx = {};
        for (int i = 0; i < 3; i++) {
            for (int j = i + 1; j < 3; j++) {
                mx = std::max(mx, e[i] + e[j]);
            }
        }
        ll cnt{};
        for (int i = 0; i < 3; i++) {
            for (int j = i + 1; j < 3; j++) {
                cnt += (mx == e[i] + e[j]);
            }
        }
        ans = ans * cnt % mod;
    }
    CNM::init();
    std::cout << (CNM::C(n / 3, n / 6) * ans) % mod;
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    solve();
    return 0;
}