原题链接

难度：$middle$

2023/2/17 每日一题

---

题目描述

给你一个由若干 $0$ 和 $1$ 组成的二维网格 $grid$，请你找出边界全部由 $1$ 组成的最大 正方形 子网格，并返回该子网格中的元素数量。如果不存在，则返回 $0$。

示例 1：

输入：grid = [[1,1,1],[1,0,1],[1,1,1]]
输出：9
复制示例输入

示例 2：

输入：grid = [[1,1,0,0]]
输出：1
复制示例输入

提示：

• $1<=grid.length<=100$
• $1<=grid[0].length<=100$
• $grid[i][j]$ 为 $0$ 或 $1$

---

算法

(模拟、前缀和) $O(n^3)$

1.我们枚举每一个子正方形：三重循环，第一重循环枚举正方形的长度 len，第二三重循环枚举左上角的顶点。
2. 我们通过前缀和来计算每个正方形的周长。
3. 我们用最外面的正方形 - 里面的正方形，可以得到最外面一圈的正方形的周长，判断是不是等于 4 * (len - 1)，如果相等，返回正方形的面积，否则返回 0。

---

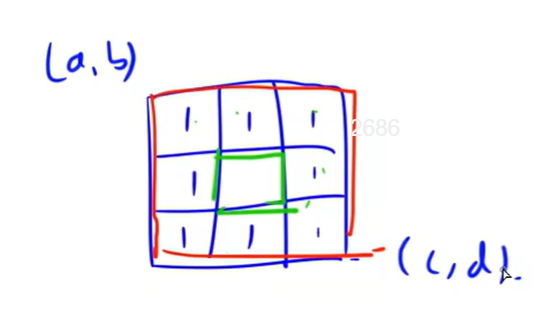
求出红色框和黄色框中间的一圈的前缀和就是正方形的周长。

---

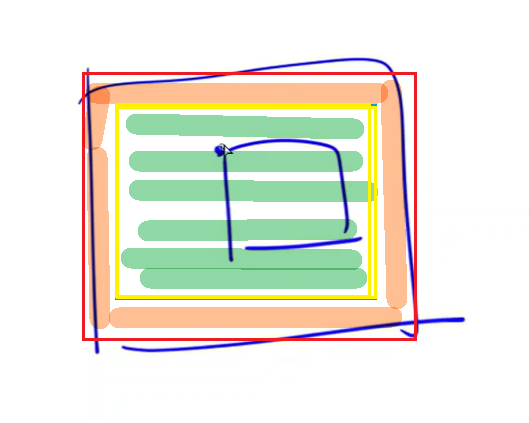
用前缀和的差可以直接计算：

C++ 代码

class Solution {
public:
    vector<vector<int>> s;

    int get(int x1, int y1, int x2, int y2) {
        return s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1];
    }
    int largest1BorderedSquare(vector<vector<int>>& grid) {
        int n = grid.size(), m = grid[0].size();
        s = vector<vector<int>>(n + 1, vector<int>(m + 1, 0));

        for (int i = 1; i <= n; i ++)
            for (int j = 1; j <= m; j ++)
                s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + grid[i - 1][j - 1];

        for (int len = min(m, n); len > 1; len --){
            for (int i = 1; i + len - 1 <= n; i ++) {
                for (int j = 1; j + len - 1 <= m; j ++) {
                    int a = i, b = j, c = i + len - 1, d = j + len - 1;
                    if (get(a, b, c, d) - get(a + 1, b + 1, c - 1, d - 1) == 4 * (len - 1))
                        return len * len;
                }
            }
        }

        if (s[n][m] > 0) return 1;
        
        return 0;
    }
};