2023美国大学生数学建模竞赛(美赛)思路&代码
- 报名
- 时间节点
- 比赛说明
- 问题A(数据分析题):收干旱影响的植物群落(MCM)
- 第一问
- 第二问
- 问题B(仿真建模题):重塑马赛马拉(MCM)
- 问题C(数据挖掘题):预测World结果(MCM)
- 问题D(交叉网络建模题):确定联合国可持续发展目标的优先级(ICM)
- 问题E(综合评价与仿真题):光污染(ICM)
- 问题F(综合评价与统计建模题):绿色GDP(ICM)
- 七.资料
报名
官方网址:http://www.comapmath.com/MCMICM/index.html
时间节点
1.官方报名截止时间:2023 年2 月17 日上午0点
2.比赛开始时间:2023 年2 月17 日上午6点
3.比赛结束时间:2023 年2 月21 日上午9点
比赛说明
- 赛题原版(英文版)下载链接:
链接:https://pan.baidu.com/s/1B9iyrSBtI4Nu1scMu_2y9Q?pwd=4ncw
提取码:4ncw- 赛题翻译(中文版)下载链接:2022年数学建模美赛翻译(校苑数模中文版)
- 赛题翻译(校苑数模中文版)下载链接:
链接:https://pan.baidu.com/s/1oQ9lIx4WCdLtDfLGfpP6QA?pwd=ifmg
提取码:ifmg
问题A(数据分析题):收干旱影响的植物群落(MCM)
- 赛题目的:分析干旱程度与植物群落中物种数量的关系
- 赛题解读&解题思路链接:
(1)这道题的难点是寻找数据,如果能找到干旱程度的适应性代表的指标以及对应植物群落物种的数量,那这道题基本上是迎刃而解,只需要简单去搭建一个预测模型即可仿真
(2)目标是对马萨马拉这个大型野生动物保护区进行推荐不同区域的管理策略

第一问
1.问题定义
- 目标函数Y:植物群落的总占地面积+群落内各类植物的数量(需要归一化量纲,不同植物体积不同,总数量不同)
- 影响因素:天气因素(是否干旱,此处量化为降水量R与太阳光功率S)、物种的种类数量 物种之间的相互作用(比如相关性,共生性)
- 物种之间的相互作用:为同类植物,则相关性较强,不同类植物相关性较弱,相关性的量化可以参照植物种类大纲,定义相关性指标系数 ,相互作用因子 ,通过拟合得到
- 定义此指标的目的就在于为了使模型更具有普遍性和适用性不同地区物种不同,A地可能大多是仙人掌之类但是B地是树木灌丛类。同一模型可以针对多种自然环境,增加模型的适用性。物种之间的正面影响因素,物种之间的负面影响因素。
- 太阳光功率可以用(一天之内温度的总和*Aera)
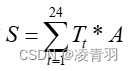
一般来讲R与S成负相关 (自己加个小模型验证就可以)
- 太阳光功率在一天内的变化:
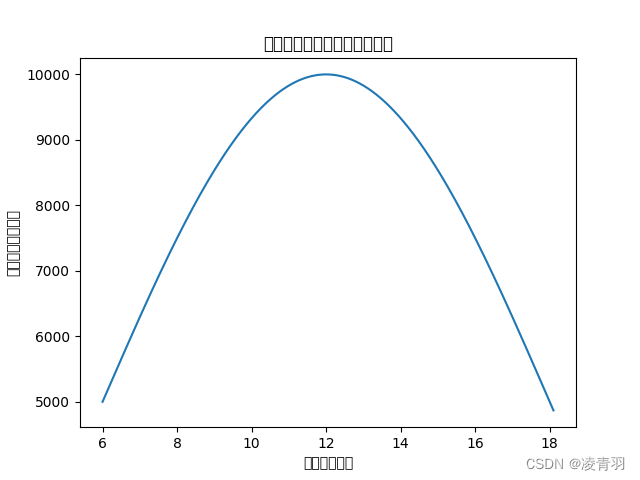
优化模型:计算一天的太阳光功率需要考虑太阳辐射的强度和时间的变化。太阳辐射的强度与太阳高度角、大气透过率、地球表面倾角等因素有关,因此需要进行一定的模拟和计算。
以下是一个示例代码,展示如何使用Python计算一天的太阳光功率:
import numpy as np
# 太阳直射辐射强度,单位:瓦/平方米
solar_constant = 1367
# 太阳高度角和方位角的范围,单位:弧度
altitude_range = np.arange(-np.pi/2, np.pi/2+0.01, 0.01)
azimuth_range = np.arange(-np.pi, np.pi+0.01, 0.01)
# 地球自转周期,单位:小时
day_length = 24
# 日内时刻,从早上6点到晚上6点,每隔10分钟记录一次
time_range = np.arange(6, 18.1, 0.01)
# 计算每个时刻的太阳光功率
solar_power = []
for t in time_range:
# 计算太阳高度角和方位角
hour_angle = (t-12)/12 * np.pi
declination = 23.45 * np.sin(2*np.pi*(284+t)/365)
altitude = np.arcsin(np.sin(declination)*np.sin(23.45*np.pi/180) + np.cos(declination)*np.cos(hour_angle)*np.cos(23.45*np.pi/180))
azimuth = np.arccos((np.sin(declination)*np.cos(altitude)-np.sin(altitude)*np.cos(23.45*np.pi/180))/(np.cos(altitude)*np.sin(23.45*np.pi/180)))
if hour_angle > 0:
azimuth = -azimuth
# 计算太阳直射辐射强度
cos_theta = np.sin(altitude)*np.sin(30*np.pi/180) + np.cos(altitude)*np.cos(30*np.pi/180)*np.cos(azimuth-(-np.pi/2))
tau = 0.7**((altitude*180/np.pi)/10)
s = solar_constant * cos_theta * tau
if np.isnan(s):
continue
solar_power.append(s)
# 将每个时刻的太阳光功率相加,得到一天的太阳光功率
daily_solar_power = np.sum(solar_power) * day_length * 60 * 60
print('一天的太阳光功率为:%.2f千瓦时' % (daily_solar_power/1000))
结果:
一天的太阳光功率为:18506091.09千瓦时
2.建立预测函数
根据查询的文献:建立预测函数(此函数自己定义,也可以根据预测模型,定义线性关系,高阶拟合,乃至指数拟合,本人建议用指数拟合)(聚类分析也可):
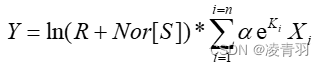
2.1 拟合函数方式
为了拟合给定的函数,我们需要导入相应的库,这里我们将使用 numpy 和 scipy 库来进行拟合和评估模型的准确度。具体步骤如下:
1.首先,我们需要定义给定的函数,这里是 y = ln(R + S) * Σ(i=1 to n)(a * exp(K[i]) * x[i])。
2.接下来,我们需要准备训练数据和测试数据,可以使用 numpy 库生成一些随机数据。
3.然后,我们需要定义误差函数,即预测值与实际值之间的差距,这里我们使用均方根误差(RMSE)作为误差函数。
4.然后,我们可以使用 scipy.optimize.curve_fit() 函数来拟合给定的函数,该函数可以返回最优拟合参数。
5.最后,我们可以使用训练数据和测试数据来评估模型的准确度,可以使用 RMSE 和 R 平方值来评估。
import numpy as np
from scipy.optimize import curve_fit
from sklearn.metrics import mean_squared_error, r2_score
# 定义给定的函数
def func(x, a, R, S, K1, K2, K3, K4):
return np.log(R + S) * (a * np.exp(K1 * x[0]) + a * np.exp(K2 * x[1]) + a * np.exp(K3 * x[2]) + a * np.exp(K4 * x[3]))
# 准备数据
x_train = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12], [13, 14, 15, 16], [17, 18, 19, 20]])
y_train = np.array([3, 5, 7, 9, 11])
x_test = np.array([[21, 22, 23, 24], [25, 26, 27, 28], [29, 30, 31, 32], [33, 34, 35, 36], [37, 38, 39, 40]])
y_test = np.array([13, 15, 17, 19, 21])
# 定义误差函数(均方根误差)
def rmse(y_true, y_pred):
return np.sqrt(mean_squared_error(y_true, y_pred))
# 初始猜测值
initial_guess = [1, 1, 1, 1, 1, 1, 1]
# 拟合函数
popt, pcov = curve_fit(func, x_train.T, y_train, p0=initial_guess)
# 输出拟合参数
print("拟合参数:", popt)
# 预测测试数据
y_pred = func(x_test.T, *popt)
# 输出测试数据的均方根误差和 R 平方值
print("测试
2.2 深度学习方法
- 随机数生成数据的方式作为模拟,误差比较大,用的时候换成自己的数据就可以了
- 换成excel数据
具体代码见链接:2023美赛A题:收干旱影响的植物群落(MCM)思路&Python代码
3.结果分析
1、预测结果的准确图,较优的拟合结果。
2、降水正常图和降水异常图对比
3、相互作用图,通过得到降水正常的年份和异常年份相互作用因子
第二问
- 发现与结果出入较大,发现物种之间有正相关有负相关
- 加入影响因子 (因为有的物种是正影响,有的是负面影响,指数函数均为正影响)去修正模型,得到拟合数据更加贴近真实数据,此处一步步推进,得到更复杂更优质的模型。
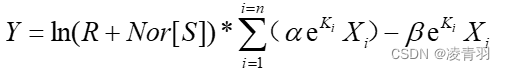
问题B(仿真建模题):重塑马赛马拉(MCM)
太阳光功率可以用(一天之内温度的总和*Aera),即 ,一般来讲R与S成负相关 (自己加个小模型验证就可以)
- 赛题目的:对马赛马拉这个大型野生动物保护区进行推荐不同区域的管理策略,可以通过了解各个区域的特点,建立有效的监测和评估机制,然后通过设置一些仿真条件,根据实际情况采取不同的管理策略
- 赛题解读&解题思路链接:难点主要是如何构建动物园各区域仿真模型与设置有效的评估机制。
问题C(数据挖掘题):预测World结果(MCM)
- 赛题目的:通过分析wordle的游戏机制,挖掘不同单词所对应的得分情况对其难度的影响
- 赛题解读&解题思路链接:这道题的难度主要是如何提取不同单词难度的特征,相对来说反而是最好实现的。
问题D(交叉网络建模题):确定联合国可持续发展目标的优先级(ICM)
- 赛题目的:对联合国制定的17个可持续发展目标进行关系网络的构建同时评估其可能存在的影响
- 赛题解读&解题思路链接:交叉网络回归路径分析,如何寻找到能代表可持续发展目标的数值是这道题的难点。
问题E(综合评价与仿真题):光污染(ICM)
- 赛题目的:针对光污染,进行度量评价以及模拟出四个位置进行干扰策略的影响分析
- 赛题解读&解题思路链接:如何收集到数据对这四个地方进行仿真,一个最简单的方法是直接通过佳能相机去到这四个定义的地方获取其光源度量值。
问题F(综合评价与统计建模题):绿色GDP(ICM)
- 赛题目的:针对使用Ggdp替代GDP的国家经济健康带来的好处分析
- 赛题解读&解题思路链接:相对收集数据容易
大家不管看了谁的翻译文件(大部分都是机器翻译),英文版的一定要自己再看一遍,逐字推敲。
推荐大家一个很方便的PDF翻译软件(我们研究生经常用来看英文文献的):知云文献翻译(可以在微信里面搜索,下载软件安装包)或者登录官网:https://www.zhiyunwenxian.cn/
七.资料
1)往年优秀论文:美国大学生数学建模竞赛2004-2020年优秀论文汇总
2)各赛题的代码汇总:美赛各题常用算法程序与参考代码.rar
注:第一次参加数学建模比赛的,推荐看一下这篇文章:
如何在数学建模比赛中稳拿奖——个人100%获奖经历分享