已知
2
c
o
s
2
+
3
c
o
s
a
s
i
n
a
−
3
s
i
n
2
a
=
1
,
并且
a
∈
(
−
3
2
π
,
−
π
)
2cos^{2}+3cosasina-3sin^{2}a=1 ,并且a\in(-\frac{3}{2}\pi,-\pi)
2cos2+3cosasina−3sin2a=1,并且a∈(−23π,−π)
求
2
s
i
n
(
π
−
a
)
−
3
s
i
n
(
π
2
+
a
)
)
4
s
i
n
a
−
9
c
o
s
a
\frac{2sin(\pi-a)-3sin(\frac{\pi}{2}+a))}{4sina-9cosa}
4sina−9cosa2sin(π−a)−3sin(2π+a))
chatGPT回复:
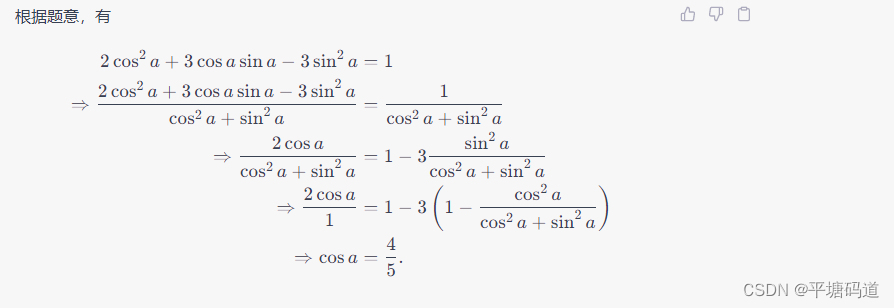
注意到 a ∈ ( − 3 2 π , − π ) a\in(-\frac{3}{2}\pi,-\pi) a∈(−23π,−π),因此 sin a < 0 \sin a<0 sina<0。然后有
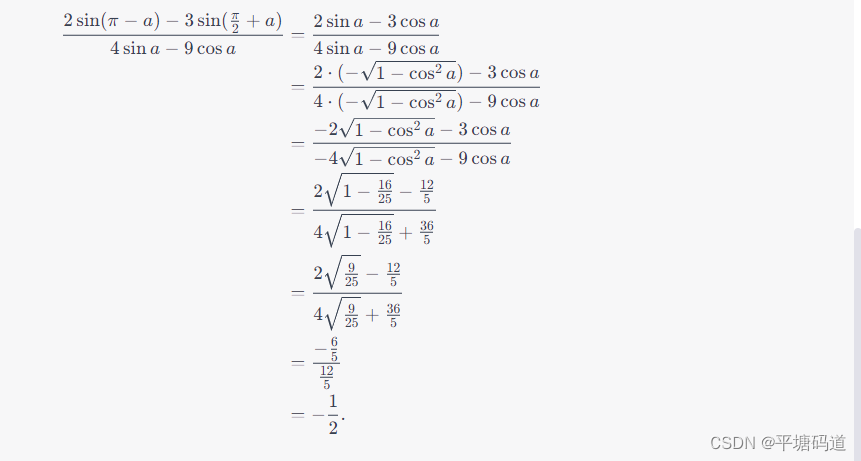
因此 2 sin ( π − a ) − 3 sin ( π 2 + a ) 4 sin a − 9 cos a = − 1 2 \dfrac{2\sin(\pi-a)-3\sin(\frac{\pi}{2}+a)}{4\sin a-9\cos a}=-\dfrac{1}{2} 4sina−9cosa2sin(π−a)−3sin(2π+a)=−21。