题目：

任意给定一个正整数N，

如果是偶数，执行： N / 2

如果是奇数，执行： N * 3 + 1

生成的新的数字再执行同样的动作，循环往复。

通过观察发现，这个数字会一会儿上升到很高，

一会儿又降落下来。

就这样起起落落的，但最终必会落到“1”

这有点像小冰雹粒子在冰雹云中翻滚增长的样子。

比如N=9

9,28,14,7,22,11,34,17,52,26,13,40,20,10,5,16,8,4,2,1

可以看到，N=9的时候，这个“小冰雹”最高冲到了52这个高度。

输入格式：

一个正整数N（N<1000000）

输出格式：

一个正整数，表示不大于N的数字，经过冰雹数变换过程中，最高冲到了多少。

例如，输入：

10

程序应该输出：

52

再例如，输入：

100

程序应该输出：

9232

资源约定：

峰值内存消耗（含虚拟机） < 256M

CPU消耗 < 1000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入...” 的多余内容。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。

注意：不要使用package语句。不要使用jdk1.7及以上版本的特性。

注意：主类的名字必须是：Main，否则按无效代码处理。

分析：

这个题非常容易因为没有注意到这句话表示不大于N的数字导致粗心做错，我们先来做一遍经常犯的错误示范

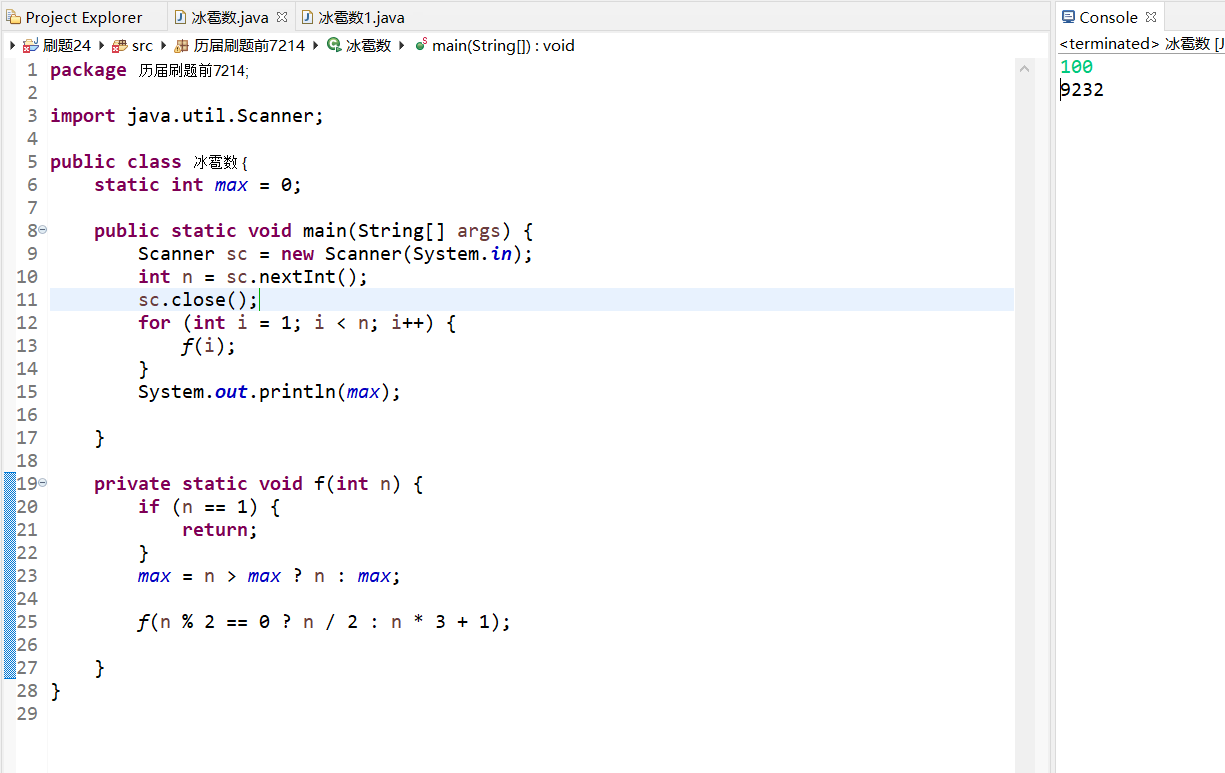
1，输入n的值然后通过递归做这道题，由题意得，递归的结束条件是当n等于1时结束，如果n为偶数，那么n/2；如果为奇数n*3+1,那我们就一直调用自身直到n等于1(结束条件)为止，并在这个过程中不断的把n相对大的值给max，结束循环。输出max就是冰雹最高高度

如下图：

我们发现当n等于10的时候n等于16，n=100的时候输出100，都跟题意相差很大，那么我们重新读题，第二遍读题中发现

输出的不是n的变化过程，而是n之前的数字（包括n）就比如说n=10，输出就是1-10这十个数字每个都要进行变换，然后取这十个数字变化过程的最大值。那么我们就需要根据n的值建一个for循环，循环n次。

下面是完整正确步骤：

完整步骤：

package 历届刷题前7214;

import java.util.Scanner;

public class 冰雹数 {
    static int max = 0;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        sc.close();
        for (int i = 1; i < n; i++) {
            f(i);
        }
        System.out.println(max);

    }

    private static void f(int n) {
        if (n == 1) {
            return;
        }
        max = n > max ? n : max;

        f(n % 2 == 0 ? n / 2 : n * 3 + 1);

    }
}