UVa 1343 The Rotation Game 旋转游戏 IDA* BFS 路径还原

news2024/9/30 19:30:33

题目链接：The Rotation Game
题目描述：

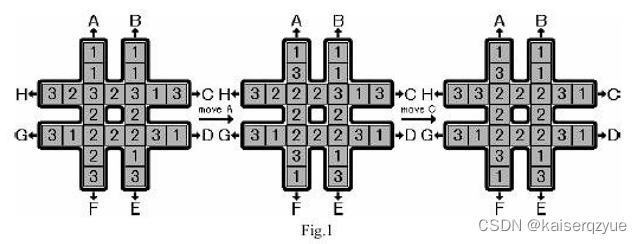
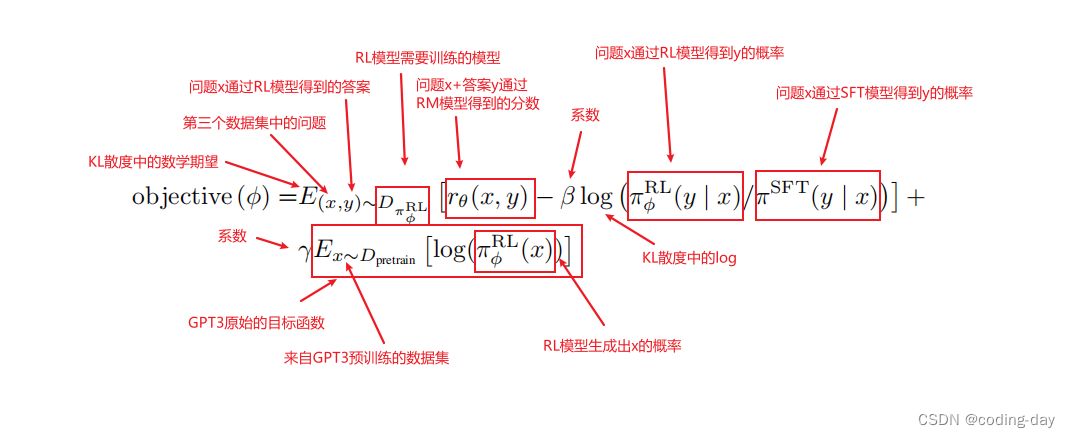
给定二十四个整数，这二十四个整数由八个一，八个二，八个三组成，从左到右，从上到下依次描述下图方格中的数字：

例如上图左边对应的输入就是 $[1, 1, 1, 1, 3, 2, 3, 2, 3, 1, 3, 2, 2, 3, 1, 2, 2, 2, 3, 1, 2, 1, 3, 3]$ 。你每一次可以进行 $A - H$ 八种操作，上图给出了 $A$ 操作和 $C$ 操作如何进行，其他的操作如何进行可以类似的推出，你的任务是找到最少的操作步数让中间的八个数字为同一个数字，例如上图左边经过两次操作能将中间全部变成 $2$ ，如果有多个解，那么你需要输出字典序最小的解，同时你还需要输出中间的数字。

题解：

本题可以使用 $I D A * (I t er a t i v eDee p e nin g A St a r)$ 算法，直接依次枚举进行的操作（需要注意的是，应该先枚举字典序小的），很明显可以发现，每一次移动最多只会让中间的位置正确的数字个数增加一，所以可以考虑的剪枝是：最大深度与当前深度之差如果小于中间最少的不对的数字时进行剪枝。
当然本题还有其他的做法。
本题也可以通过 $BFS$ 来做，不过使用 $BFS$ 来解决本题的时候，我们可以转换一下思路，我们可以把目标状态能够到达的所有其他状态枚举出来，这样的花费与从某个状态到目标状态是一样的。但是这样枚举存在一个问题：时间复杂度过高。
时间复杂度如何计算？要计算时间复杂度也就是计算所有可能的状态，也就是计算 $24$ 个数字，这 $24$ 个数字含有三种数字，每种数字的个数均为 $8$ 的排列个数，那么根据高中的组合数学知识，我们可以知道可能的排列个数为 $\frac {24!} {8!8!8!}$ ，这个数字是比较大的。不过我们有新的方法，因为只需要中间的八个数字相同，我们可以依次枚举中间可能的数字(这里是 $1, 2, 3$ )，不同于中间可能的数字记为 $0$ ，这样可能状态数量就变成了 $24$ 个数字包含两种数字，其中一种数字的个数是 $8$ ，另一个种数字的个数是 $16$ 的排列个数，那么此时的排列个数变成了 $\frac {24!} {8!16!}$ 此时的复杂度就到了可以接受的范围了。我们在 $BFS$ 完成之后可以不用存储每一次的路径，而是在后续来还原出路径，这样可以节省一定的空间开销，还原的过程类似于 $BFS$ 的过程，只是还原的时候只会访问最佳的路径，而不是所有的路径。同时在 $BFS$ 的时候，由于在队列中放入一个数组非常不好处理，所以我们需要将状态进行编码，由于一共只有 $24$ 个状态，那么我们可以用 $24$ 位的二进制数来表示每一个位置的状态。
经过测试 $I D A *$ 速度要快得多。

IDA*代码：

#include <bits/stdc++.h>

using namespace std;

int g[24];
vector<char> ans;

// 数据的下标 6 7 8 11 12 15 16 17为中间的八个数字
// 返回最少需要几个数字让中间八个数字相同
int getWrongPos()
{
    int cnt[4] = {0};
    cnt[g[6]]++;
    cnt[g[7]]++;
    cnt[g[8]]++;
    cnt[g[11]]++;
    cnt[g[12]]++;
    cnt[g[15]]++;
    cnt[g[16]]++;
    cnt[g[17]]++;
    return 8 - max(cnt[1], max(cnt[2], cnt[3]));
}

void move(int op)
{
    int temp = 0;
    switch(op) {
        case 0:
            temp = g[0];
            g[0] = g[2];
            g[2] = g[6];
            g[6] = g[11];
            g[11] = g[15];
            g[15] = g[20];
            g[20] = g[22];
            g[22] = temp;
            break;
        case 1:
            temp = g[1];
            g[1] = g[3];
            g[3] = g[8];
            g[8] = g[12];
            g[12] = g[17];
            g[17] = g[21];
            g[21] = g[23];
            g[23] = temp;
            break;
        case 2:
            temp = g[10];
            for (int i = 10; i >= 5; i--) { g[i] = g[i - 1]; }
            g[4] = temp;
            break;
        case 3:
            temp = g[19];
            for (int i = 19; i >= 14; i--) { g[i] = g[i - 1]; }
            g[13] = temp;
            break;
        case 4:
            temp = g[23];
            g[23] = g[21];
            g[21] = g[17];
            g[17] = g[12];
            g[12] = g[8];
            g[8] = g[3];
            g[3] = g[1];
            g[1] = temp;
            break;
        case 5:
            temp = g[22];
            g[22] = g[20];
            g[20] = g[15];
            g[15] = g[11];
            g[11] = g[6];
            g[6] = g[2];
            g[2] = g[0];
            g[0] = temp;
            break;
        case 6:
            temp = g[13];
            for (int i = 13; i <= 18; i++) { g[i] = g[i + 1]; }
            g[19] = temp;
            break;
        case 7:
            temp = g[4];
            for (int i = 4; i <= 9; i++) { g[i] = g[i + 1]; }
            g[10] = temp;
            break;
        default:
            return;
    }
}

void undoMove(int op)
{
    if (op % 2 == 0) { move((op + 5) % 8); }
    else { move((op + 3) % 8); }
}

bool dfs(int nowDepth, int maxDepth)
{
    int wrongPos = getWrongPos();
    if (nowDepth == maxDepth) { return wrongPos == 0; }
    if (maxDepth - nowDepth < wrongPos) { return false; }
    for (int i = 0; i < 8; i++) { // 要求字典序最小只需要从小到大枚举即可
        ans.push_back(i + 'A');
        move(i);
        if (dfs(nowDepth + 1, maxDepth)) { return true; }
        undoMove(i);
        ans.pop_back();
    }
    return false;
}

int main()
{
    ios::sync_with_stdio(false);
    while (cin >> g[0] && g[0] != 0) {
        for (int i = 1; i < 24; i++) { cin >> g[i]; }
        ans.resize(0);
        for (int maxDepth = 0; ; maxDepth++) {
            if (dfs(0, maxDepth)) {
                if (maxDepth == 0) {
                    cout << "No moves needed" << endl << g[6] << endl;
                } else {
                    for (auto ch : ans) { cout << ch; }
                    cout << endl << g[6] << endl;
                }
                break;
            }
        }
    }
    return 0;
}

BFS代码：

#include <bits/stdc++.h>

const int INF = 0x3f3f3f3f;

using namespace std;

int g[24];
int finalStatus[] = {0, 0,
                     0, 0,
             0, 0, 1, 1, 1, 0, 0,
                   1,    1,
             0, 0, 1, 1, 1, 0, 0,
                     0, 0,
                     0, 0};
int finalStatusEncode, ansDis, ans;
map<int, int> dis;
string ansStr; // 这里改成string可以方便的比较大小

int encode(int *status, int number)
{
    int statusEncode = 0;
    for (int i = 0; i < 24; i++) { statusEncode |= (status[i] == number ? (1 << i) : 0); }
    return statusEncode;
}

void decode(int statusEncode, int *status)
{
    for (int i = 0; i < 24; i++) { status[i] = (statusEncode & (1 << i)) >> i; }
}

void move(int op, int *g); //该函数与IDA*中一样，这里不再给出

void bfs()
{
    finalStatusEncode = encode(finalStatus, 1);
    queue<int> q;
    q.push(finalStatusEncode);
    dis[finalStatusEncode] = 0;
    while(!q.empty()) {
        int nowStatus = q.front();
        q.pop();
        for (int i = 0; i < 8; i++) {
            decode(nowStatus, g); // 先解码，解码的目的是为了进行移动操作
            move(i, g);
            int newStatus = encode(g, 1);
            if (dis.count(newStatus) == 0) {
                dis[newStatus] = dis[nowStatus] + 1;
                q.push(newStatus);
            }
        }
    }
}

void getPath()
{
    int gTemp[24] = {0};
    for (int number = 1; number <= 3; number++) {
        int nowStatus = encode(g, number);
        if (ansDis == dis[nowStatus]) {
            string nowStr;
            while (nowStatus != finalStatusEncode) {
                for (int i = 0; i < 8; i++) {
                    decode(nowStatus, gTemp);
                    move(i, gTemp);
                    int newStatus = encode(gTemp, 1);
                    if (dis.count(newStatus) == 1 && dis[newStatus] + 1 == dis[nowStatus]) { // 在最短路径上
                        nowStatus = newStatus;
                        nowStr.push_back(i + 'A');
                        break;
                    }
                }
            }
            if (nowStr < ansStr) {
                ansStr = nowStr;
                ans = number;
            }
        }
    }
}

int main()
{
    ios::sync_with_stdio(false);
    bfs();
    while (cin >> g[0] && g[0] != 0) {
        for (int i = 1; i < 24; i++) { cin >> g[i]; }
        ansDis = INF;
        ansStr = "Z"; // "Z"比所有可能的答案的字典序都要大
        for (int number = 1; number <= 3; number++) { // 分别枚举中间的数字
            int status = encode(g, number);
            ansDis = min(ansDis, dis[status]); // 题目一定是有解的
        }
        if (ansDis == 0) {
            cout << "No moves needed" << endl << g[6] << endl;
        } else {
            getPath();
            cout << ansStr << endl << ans << endl;
        }
    }
    return 0;
}