一、前缀和的概念

• 数组a[0]~ a[n-1]，前缀和sum[i]等于a[0] ~ a[i]的和:

sum[0] = a[0]

sum[1] = a[0] + a[1]

sum[2] = a[0] + a[1] +a[2] ......

• 在O(n)时间内求所有前缀和:

sum[i] = sum[i-l] +a[i]

• a[0]一般不用。

二、前缀和与区间问题

• 预计算出前缀和，能快速计算出区间和:

a[i] + a[i+1] + ... + a[j-1] + a[j] = sum[j]- sum[i-1]

• 复杂度为O(n)的区间和计算，优化到了O(1)的前缀和计算。

• 二分法是一种求解的方法。

三、前缀和与差分

• 维差分数组 D[k] = a[k] - a[k-1]，即原数组a[]的相邻元素的差。

• a[k]= D[1]+ D[2]+ ... + D[k]

• a[ ]是D[ ]的前缀和。

• 差分是前缀和的逆运算: 把求a[k]转化为求D的前缀和。

四、差分数组: 提升修改的效率

• 把区间[L,R]内每个元素a[ ]加上d，只需把对应的D[ ]做以下操作:

• 把D[L]加上d------>D[L] += d

• 把D[R+1]减去d------>D[R+1] -= d

• 利用D[ ]，能极快解决修改区间[L,R]内元素的目的 。原来需要O(n)次计算，现在只需要O(1)。

• 说明:前缀和a[x]= D[1] + D[2] + ... + D[x]，有:

• 1≤x≤L，前缀和a[x]不变;

• L≤x≤R，前缀和a[x]增加了d;

• R≤x≤N，前缀和a[x]不变，因为被D[R+1]中减去的d抵消了

五、真题实例(196号)

---

• 题意

给定一个数组a[ ]，一次操作是对连续的3个数做加减，经过多次操作后得到的数组，其中有一个数的绝对值最大；问这个最大的绝对值能达到多小。

• 思考

• 所有加减操作都是在数组内部进行，对于整个数组的和不会有影响。

• 一次操作是对连续的3个数a[i-1]、a[i]、a[i+1]，根据：

a[1] = a[1]+a[2]

a[3] = a[3]+a[2]

a[2] = a[2]-2a[2]

• 三个数的和不变，由此联想前缀和。

• 一次操作后的前缀和:

a[i-1]更新为a[i] + a[i-1],s[i-1]的新值等于原来的s[i]。

a[i]更新为-a[i],s[i]的新值等于原来的s[i-1]。

a[i+1]更新为a[i] + a[i+1],s[i+1]的值保持不变。

• 结论：经过一次操作后，s[i]和s[i-1]互相交换，s[i+1]不变，s[i-1]、s[i]、s[i+1]这3个数值还在，没有出现新的数值。

• 题目中对a[ ]的多次操作后的一个结果，对应了前缀和s[ ]的一种排列。

• 因为a[i] = s[i]- s[i-1]，对a[ ]多次操作后，新的a[ ]是:

a[1]= s[1]- s[0]，a[2]= s[2] - s[1]，......，a[n] = s[n] - s[n-1]

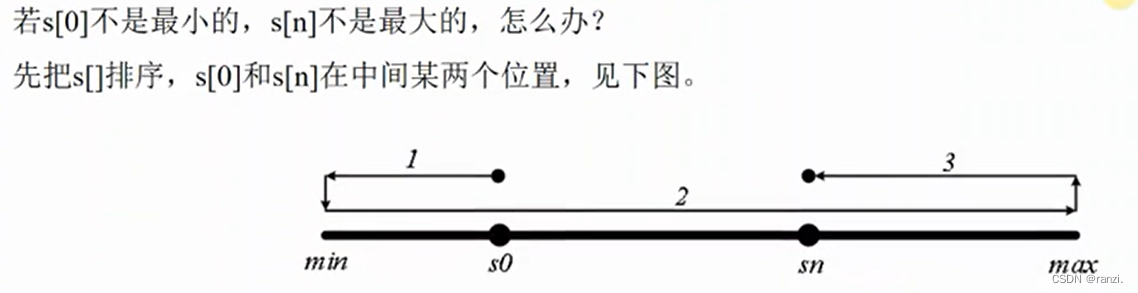
• 经过以上转换，题目的原意:“对连续3个数做加减操作后，求最大的al能达到多小”,变成了简单问题:“数组s[ ]，求max{|s[1]-s[0],|s[2]-s[1]|,.., |s[n] -s[n-1]|}，且尽量小”，s[0]和s[n]保持不动，其他s[ ]可以随意变换位置。

• 代码

• 解析

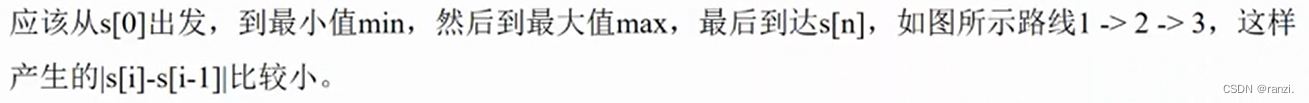
• 代码