参考:
- 双线性插值的理论
- Pytorch grid_sample解析
- PyTorch中grid_sample的使用方法
- pytorch中的grid_sample()使用
查阅官方文档,TORCH.NN.FUNCTIONAL.GRID_SAMPLE
grid_sample的函数签名如下所示,torch.nn.functional.grid_sample(input, grid, mode='bilinear', padding_mode='zeros', align_corners=None)。
在4D情况下,
- input (Tensor) – input of shape ( N , C , H i n , W i n ) (N, C, H_{in}, W_{in}) (N,C,Hin,Win),相当于输入的是图片,N为batch_size,C为channel。
- grid (Tensor) – flow-field of shape
(
N
,
H
o
u
t
,
W
o
u
t
,
2
)
(N, H_{out}, W_{out}, 2)
(N,Hout,Wout,2),最后1维一定是长度为2的数组,代表二维平面上的坐标点(x,y)。
W
o
u
t
W_{out}
Wout和
H
o
u
t
H_{out}
Hout相当于查询矩阵的宽高,函数会返回在这个查询矩阵上每个坐标的采样值。采样结果取决于插值策略
mode
align_corners=True和False时,函数的行为不同,返回结果也不同。
基本例子讲解
先看一个例子。首先,输入矩阵为inp,然后创造两个矩阵new_h、new_w,并将它们合成为查询坐标矩阵grid。输出的矩阵尺寸与查询矩阵的尺寸一致。
本例只是给出大致印象,暂不涉及具体点值的计算
# This is a sample Python script.
# Press Shift+F10 to execute it or replace it with your code.
# Press Double Shift to search everywhere for classes, files, tool windows, actions, and settings.
import torch
import torch.nn.functional as F
inp = torch.arange(0, 16)
inp = inp.reshape((1, 1, 4, 4)).float()
print("inp", inp)
# inp tensor([[[[ 0., 1., 2., 3.],
# [ 4., 5., 6., 7.],
# [ 8., 9., 10., 11.],
# [12., 13., 14., 15.]]]])
out_h = 3
out_w = 3
new_h = torch.linspace(-1, 1, out_h).view(-1, 1).repeat(1, out_w)
new_w = torch.linspace(-1, 1, out_w).repeat(out_h, 1)
print("new_h", new_h)
print("new_w", new_w)
# new_h tensor([[-1., -1., -1.],
# [ 0., 0., 0.],
# [ 1., 1., 1.]])
#new_w tensor([[-1., 0., 1.],
# [-1., 0., 1.],
# [-1., 0., 1.]])
grid = torch.cat((new_w.unsqueeze(2), new_h.unsqueeze(2)), dim=2)
print("grid", grid)
#grid tensor([[[-1., -1.],
# [ 0., -1.],
# [ 1., -1.]],
#
# [[-1., 0.],
# [ 0., 0.],
# [ 1., 0.]],
#
# [[-1., 1.],
# [ 0., 1.],
# [ 1., 1.]]])
grid = grid.unsqueeze(0)
outp = F.grid_sample(inp, grid=torch.Tensor(grid), mode='bilinear', align_corners=False)
# outp = F.grid_sample(inp, grid=grid, mode='bilinear', align_corners=False)
print("outp", outp)
# outp tensor([[[[0.0000, 0.7500, 0.7500],
# [3.0000, 7.5000, 4.5000],
# [3.0000, 6.7500, 3.7500]]]])
两种align_corners设置下的函数行为
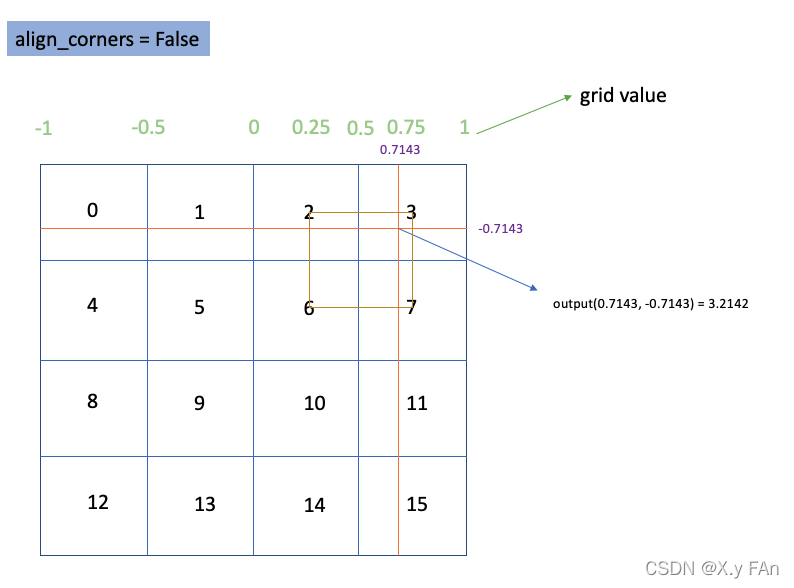
函数在接受到input参数后,会将其按照坐标位置映射到 x ∈ [ − 1 , 1 ] , y ∈ [ − 1 , 1 ] x \in [-1, 1], y \in [-1, 1] x∈[−1,1],y∈[−1,1]的矩阵范围内。而align_corners则控制了函数是否要将角落坐标的元素,映射到矩阵的角落位置。
详见Pytorch grid_sample解析。
假设输入矩阵的尺寸是4x4,元素值从0递增到15。
当align_corners=True时,input四个角落的坐标值,被映射为坐标系范围的四个角上。于是坐标(-1, -1)的值为0,(1, 1)的值为15。
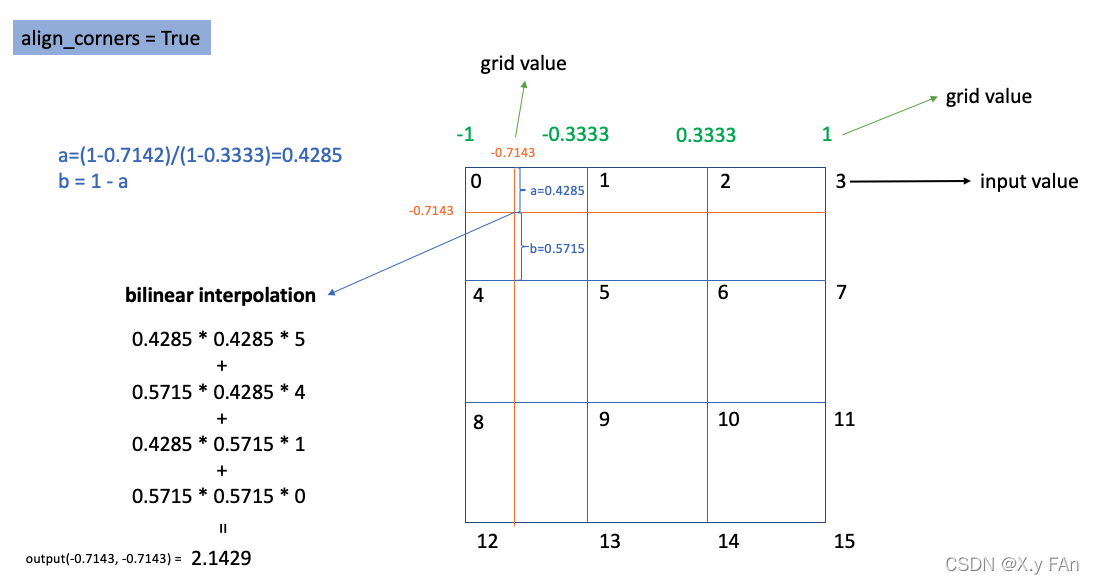
当align_corners=True时,input的每个值,会处于4x4像素矩阵的像素中心。而像素矩阵的四个角落,会被映射到坐标系范围的四个角上。
所以当要计算(0.7143, -0.7143)的值(图中红线交叉位置)时,需要先找到2,3,6,7四个值(图中褐色方框),并取他们的双线性插值。