明显看出为最小生成树，

那么：难点在哪里呢？

   if(cnt==n-k)//******
        {
            flag=1;
            break;
        }

为什么是cnt==n-k呢而不是k呢？！！！

解释：（如果每个已经连在一起了就不能分开，不管多少个连在一起的算一个棉花糖***）

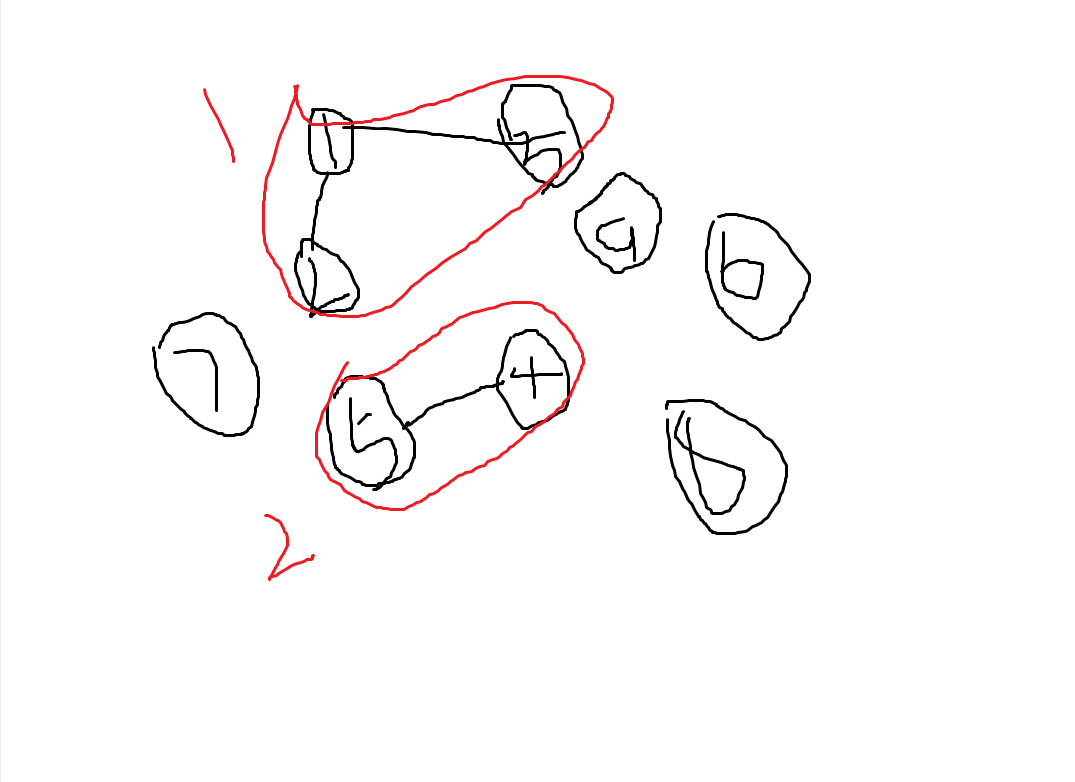
上先在有两棵树，也就是有两个棉花糖，虽然1那边有三个点连接在一起，但是它们联通了就只算一个数不能分开。以此类推

！！！：

有一句话说的是 如果n个点被n-1条边连接的话，这一定是棵树。

那么：

连的边数 得到的树的个数

n-1 1(全部点都连接在一起了)

n-2 2（还剩一个点没有连接在一起，结果就是分成两部分（一个点的，和剩下所有点的））

n-3 3（以此类推）

... ...

n-k k

所以我们如果想要连出k棵树，就需要连n-k条边。

题目要求用n朵云连出k个棉花糖。

因为每个棉花糖都是连通的，

那么每个棉花糖就相当于是一棵树。

就是说要用n个节点连出k棵树。

也就是说要用n-k条边连出k棵树。

也就是说要花费连出n-k条边的代价。

既然一定要花费连出n-k条边的代价，

那么当然要选择代价最小的边连起来。

所以给每条可以连的边按代价从小到大排个序，

然后连n-k条边造k个最小生成树就可以了。

如果给的关系数m小于需要连的边数（n-k），是一定连不出k个树来的，因为m个关系只能连m条边。

#include<iostream>
#include<algorithm>
using namespace std;
const int N=1e3+10,M=1e4+10;
struct edge{
    int u,v,w;
}e[M];
int fa[N],n,m,k;
bool cmp(edge a,edge b)
{
    return a.w<b.w; 
}
int find(int x)
{
    if(fa[x]==x)return x;
    else
    {
        fa[x]=find(fa[x]);
        return fa[x];
    }
}
int main()
{
    cin>>n>>m>>k;
    for(int i=1;i<=m;i++)
    {
        cin>>e[i].u>>e[i].v>>e[i].w;
    }
    for(int i=1;i<=n;i++)
    {
        fa[i]=i;
    }
    sort(e+1,e+1+m,cmp);
    int flag=0,cnt=0,sum=0;
    for(int i=1;i<=m;i++)
    {
        int f1=find(e[i].u);
        int f2=find(e[i].v);
        if(f1!=f2)
        {
            fa[f1]=f2;
            cnt++;
            sum+=e[i].w;
        }
        if(cnt==n-k)//******
        {
            flag=1;
            break;
        }
    }
    if(flag)
    cout<<sum;
    else
    cout<<"No Answer";
    return 0;
}