文章目录
- 整数运算
- 加法与减法
- 乘法
- 普通十进制乘法
- 硬件中实现步骤
- 例子
- 乘法器的设计
- 除法
- 普通十进制除法
- 硬件中实现步骤
- 例子
- 除法器的设计
- 浮点数运算
- 科学计数法、规格化数
- 浮点表示
- 单精度浮点数
- 双精度浮点数
- 移码表示法
- IEEE 754
- 指数偏移值(exponent bias)
- 规格化的浮点数
- 例子
- 由十进制浮点数转为二进制浮点数 -0.75
- 由二进制浮点数转为十进制浮点数
- 浮点运算
- 浮点加法减法
- 步骤
- 例子 —— 十进制 0.5 + 0.4375 使用二进制相加,假设保留 4 位精度。
- 浮点乘法
- 步骤
- 例子 —— 求 0.5 和 -0.4375 的乘积,使用二进制。
- 参考文献
整数运算
加法与减法
加减法不溢出的情况:
- 加法:当不同符号的操作数相加时,不会发生溢出,因为总和一定不会大于其中一个的操作数。例如: − 10 + 4 = − 6 -10+4=-6 −10+4=−6。
- 减法:当符号相同的操作数相减时,不会发生溢出,因为总和一定不会大于其中一个的操作数。例如: − 10 − ( − 4 ) = − 10 + 4 = − 6 -10-(-4)=-10+4=-6 −10−(−4)=−10+4=−6。
加减法溢出的情况:假设字宽为 64 位,当加或减两个 64 位的数字可能产生一个需要 65 位才能表示的结果。也就是说符号位会错位,即符号位是错误值。
溢出发生时的各种情况组合:
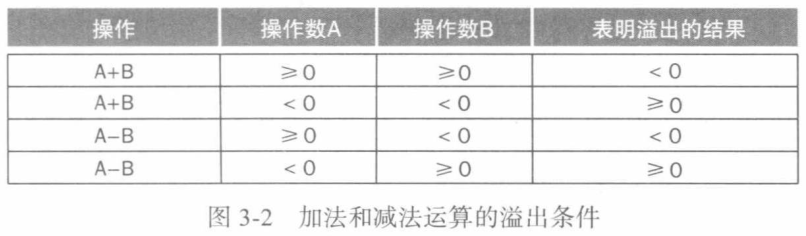
假设字宽为 8 位,即有符号数据范围为 -127~128
70+80
01000110
+ 01010000
——————————
10010110 = 150
150 达到上溢条件,因为有符号位,所以实际值为 -22
-70+(-80)
10111010
+ 10110000
——————————
101101010
超出 1 位,将最高位舍弃,保留 01101010,因此实际值位 106
无符号溢出检测:如果总和小于加数中的任何一个,则加法溢出,而如果差大于被减数,则减法溢出。
乘法
普通十进制乘法

1000 × 1001 1000 \times 1001 1000×1001 都是十进制,第一个操作数为被乘数,第二个操作数为乘数,最后的结果为积。规律:每次从右到左选择乘数中的一位,用这一位乘上被成数,然后将所得到的中间结果相对于前一位的中间结果左移一位。
硬件中实现步骤
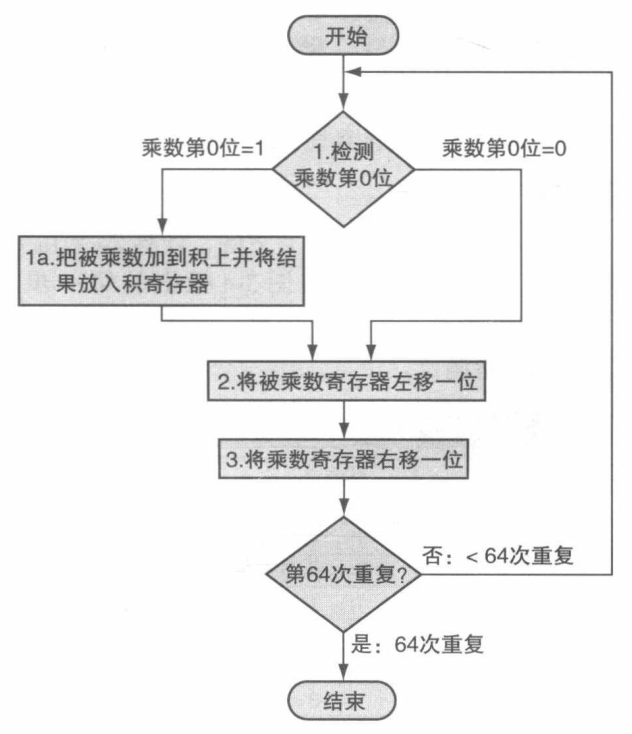
例子

乘法器的设计

除法
普通十进制除法

1001010
÷
1000
1001010 \div 1000
1001010÷1000 第一个操作是为被除数,第二个操作数为除数,结果称为商,随之产生附带结果叫做余数。它们之间个关系:
被除数
=
商
×
除数
+
余数
被除数 = 商 \times 除数 + 余数
被除数=商×除数+余数
硬件中实现步骤
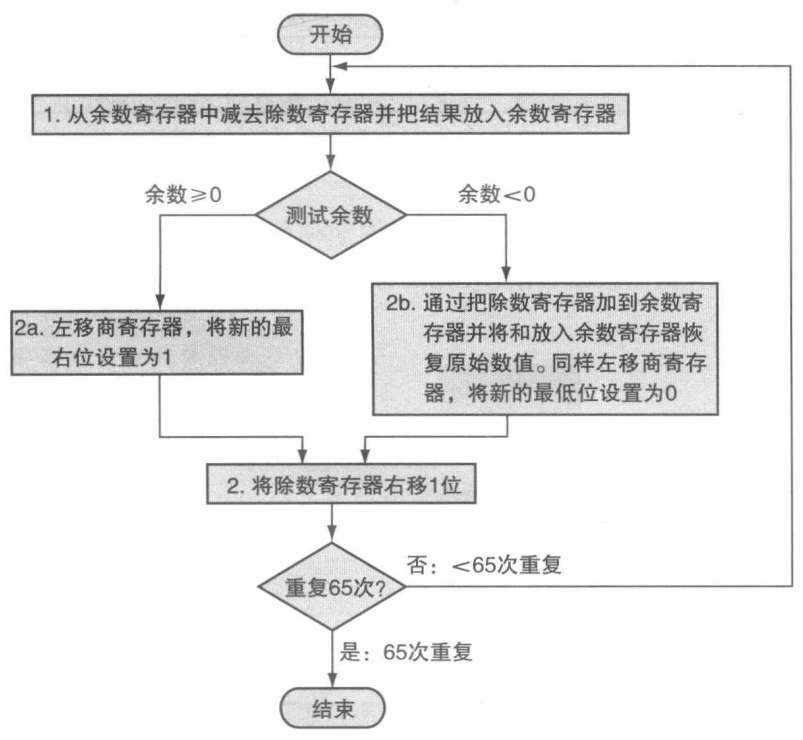
例子

除法器的设计

浮点数运算
科学计数法、规格化数
0.000000001 = > 1.0 × 1 0 − 9 0.000000001 => 1.0 \times 10^{-9} 0.000000001=>1.0×10−9
3155760000 = > 3.15576 × 1 0 9 3155760000 => 3.15576 \times 10^9 3155760000=>3.15576×109
以上两种就是科学计数法表示形式,该记数法在小数点左边只有一个数字。
科学记数法中整数部分没有前导零的数字称为规格化数。例如 1.0 × 1 0 − 9 1.0\times 10^{-9} 1.0×10−9 是规格化数,但 0.1 × 1 0 − 8 0.1 \times 10^{-8} 0.1×10−8 和 10.0 × 1 0 − 10 10.0 \times 10^{-10} 10.0×10−10 不是。
我们也可以像用科学记数法表示十进制一样来表示二进制:
(
0.1
)
2
=
>
1.
0
2
×
2
−
1
(0.1)_2 => 1.0_2 \times 2^{-1}
(0.1)2=>1.02×2−1
Tips: 小数点左边必须只剩一个非零数。
浮点表示
单精度浮点数

| 符号 | 位数 | 备注 |
|---|---|---|
| S | 1 | 表示该浮点数是否有符号。 |
| E | 8 | 指数,可以是负数的补码,偏移值为 127。 |
| F | 23 | 有效数位最左边的“1”一定存在,因此不存储该位,也就是说有效位是 24 位,实际存储 23 位。 |
通常可以这么表示:
(
−
1
)
S
×
F
×
2
E
(-1)^S \times F \times 2^E
(−1)S×F×2E
双精度浮点数
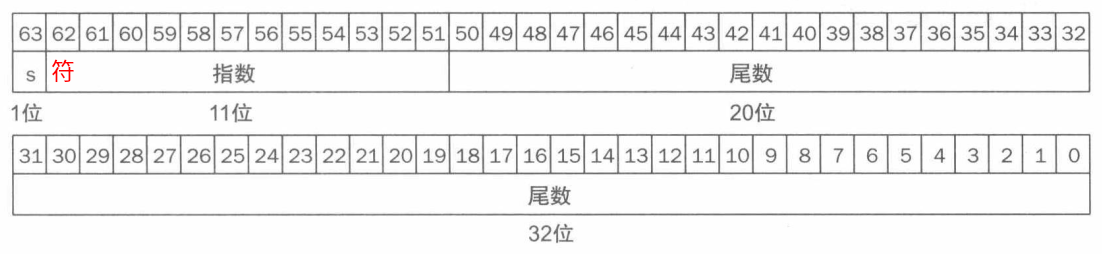
偏移值为: 2 10 − 1 = 1023 2^{10}-1=1023 210−1=1023
通常可以这么表示(注意:和上面单精度只是写法不同,实际上是一样的):
(
−
1
)
S
×
2
E
×
1.
M
(-1)^S \times 2^E \times 1.M
(−1)S×2E×1.M
fraction:小数部分(包含小数点)。
mantissa:尾数(小数点后面的数值)。
移码表示法
移码(英语:Offset binary)是一种将全0码映射为最小负值、全1码映射为最大正值的编码方案。通常对于n位二进制数,偏移量为 2 n − 1 2^n-1 2n−1。
移码在逻辑比较操作中可以得到和真值比较相同的结果,补码则当且仅当符号相同时逻辑比较操作的结果和真值比较相同,否则比较结果将颠倒(负值比正值大)。
例如:比较 120 和 -120 的大小。
120 => 01111000 原码
-120 => 10001000 补码
二进制比较规则:从左到右依次比较,若一样则跳过该位,继续比较下一位,若某一方为 1 则大。
可以发现,得到的结果是 -120 > 120 错误结果,并不是我们想要的。
接下来对 -120 用移码表示,移码=原数的补码+偏移值。
-120 移码:
= 10000000B + (-1111000B)
= 10000000B + (10001000B)
= 00001000B
Tips: 这样的移码也可以叫做偏移值为 128 的移码,也是标准移码,
最后再次进行比较:
120 => 01111000 原码
-120 => 00001000 移码
得到正确结果 120 > -120
移码主要用于表示浮点数的阶码(即指数),在浮点数运算中有优势。
IEEE 754
指数偏移值(exponent bias)
IEEE 754 标准规定该固定值为 2 n − 1 − 1 2^{n-1}-1 2n−1−1,n 是字宽。
单精度浮点数为例,它的指数域长度为 8,则固定值为 2 7 − 1 = 127 2^7-1=127 27−1=127,且该指数允许负数,则数据范围可取 [ − 126 , 127 ] [-126,127] [−126,127](127 和 128 被用作特殊值处理)。
例如指数实际值为 17,那么在单精度浮点数指数域的编码值为 144,即 144 = 127 + 17 144 = 127 + 17 144=127+17。
采用指数的实际值加上固定的偏移值的办法表示浮点数的指数,好处是可以用长度为个比特的无符号整数来表示所有的指数取值,这使得两个浮点数的指数大小的比较更为容易,实际上可以按照字典次序比较两个浮点表示的大小。(详细请看上面“移码表示法”)。
这种移码表示的指数部分,中文称作阶码。
规格化的浮点数
若浮点数中的指数部分的编码值在 0 < E ( e x p o n e n t ) < = 2 n − 2 0 < E(exponent) <= 2^n -2 0<E(exponent)<=2n−2 之间,且在科学表示法的表示下,分数部分最高有效位(即小数点左边)是 1,那么这个浮点数称为规格化浮点数。
这个规格化浮点数可表示为:
(
−
1
)
S
×
1.
M
×
2
E
−
偏移值
(-1)^S \times 1.M \times 2^{E-偏移值}
(−1)S×1.M×2E−偏移值
在规格化的浮点数下,尾数中隐藏了一位二进制有效位,隐藏了“1”,为了与二进制科学记数法尾数区别,故而 IEEE 754 将 M 称之为有效位数(significant)。
科学记数法的补充:
尾数
×
底
数
指数
尾数 \times 底数^{指数}
尾数×底数指数
例如:
1.0
1
2
×
1
0
8
1.01_2 \times 10^8
1.012×108 中尾数便是
1.0
1
2
1.01_2
1.012,而 IEEE 754 中将
0
1
2
01_2
012 称为有效位数,而隐藏了小数点前面的
1
1
1。
单精度规格化浮点数的指数值域为 00000001 到 11111110,分数部分(即小数点后面)则是 000…000 到 111…111(23-bit)。
**Tips:**为什么分数部分从 0 开始?因为规格化浮点数 1. M 1.M 1.M 隐藏了 1,只存储了 M M M。
例子
由十进制浮点数转为二进制浮点数 -0.75
用二进制小数表示:
−
0.1
1
2
-0.11_2
−0.112
用二进制科学记数法表示:
−
0.1
1
2
×
2
0
-0.11_2 \times 2^0
−0.112×20
用二进制科学记数法的规格化形式表示:
−
1.
1
2
×
2
−
1
-1.1_2 \times 2^{-1}
−1.12×2−1
接下来以单精度通常为例,计算指数:
E
=
指数
+
偏移量
=
−
1
+
127
=
126
E = 指数 + 偏移量 = -1 + 127 = 126
E=指数+偏移量=−1+127=126
其单精度表示为:
(
−
1
)
S
×
(
1
+
0.1000
0000
0000
0000
0000
00
0
2
)
×
2
126
−
127
(-1)^S \times (1+0.1000\ 0000\ 0000\ 0000\ 0000\ 000_2) \times 2^{126-127}
(−1)S×(1+0.1000 0000 0000 0000 0000 0002)×2126−127
所以 -0.75 的单精度二进制可表示为:

另外,双精度可表示为:
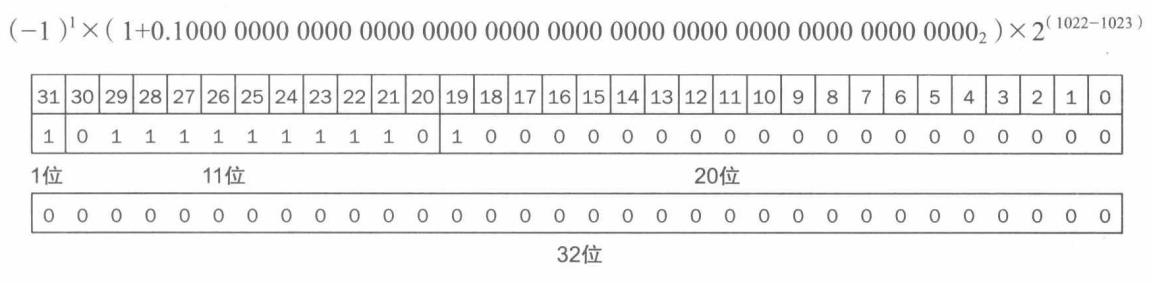
由二进制浮点数转为十进制浮点数
符号位:1,指数字段 126,尾数字段:
1
×
2
−
1
=
1
/
2
1 \times 2^{-1}=1/2
1×2−1=1/2,即 0.5。
KaTeX parse error: No such environment: eqnarray at position 8: \begin{̲e̲q̲n̲a̲r̲r̲a̲y̲}̲ & & (-1)^S \ti…
浮点运算
浮点加法减法
步骤

例子 —— 十进制 0.5 + 0.4375 使用二进制相加,假设保留 4 位精度。
KaTeX parse error: Expected 'EOF', got '&' at position 6: 0.5 &̲ = & 1.000_2 \t…
第一步:将指数较小的数(
−
1.11
0
2
×
2
−
2
-1.110_2 \times 2^{-2}
−1.1102×2−2)的有效数位右移,直到其指数与较大的数相同。
−
1.11
0
2
×
2
−
2
=
−
0.11
1
2
×
2
−
1
-1.110_2 \times 2^{-2} = -0.111_2 \times 2^{-1}
−1.1102×2−2=−0.1112×2−1
第二步:将有效位相加。
1.00
0
2
+
(
−
0.11
1
2
)
=
0.00
1
2
1.000_2 + (-0.111_2) = 0.001_2
1.0002+(−0.1112)=0.0012
1.00 0 2 × 2 − 1 + ( − 0.11 1 2 × 2 − 1 ) = 0.00 1 2 × 2 − 1 1.000_2 \times 2^{-1} + (-0.111_2 \times 2^{-1}) = 0.001_2 \times 2^{-1} 1.0002×2−1+(−0.1112×2−1)=0.0012×2−1
第三步:对和进行规格化,并检查上溢和下溢。
0.00
1
2
×
2
−
1
=
1.00
0
2
×
2
−
4
0.001_2 \times 2^{-1} = 1.000_2 \times 2^{-4}
0.0012×2−1=1.0002×2−4
单精度指数的范围是
[
−
126
,
127
]
[-126, 127]
[−126,127],因为
−
126
<
=
−
4
<
=
127
-126 <= -4 <= 127
−126<=−4<=127,所以指数合法。
第四步:对和进行舍入。
1.00 0 2 × 2 − 4 1.000_2 \times 2^{-4} 1.0002×2−4 符合保留 4 位精度的条件。
举个需要舍入的的例子,例如对 1.001 5 10 × 1 0 2 1.0015_{10} \times 10^2 1.001510×102 保留 4 位精度,现在 1.001 5 10 1.0015_{10} 1.001510 是 5 位精度,根据紧跟在第 4 位后一位的数值决定是舍还是入,得到的是 5 5 5,因此前 1 位进一得到 1.00 2 10 × 1 0 2 1.002_{10} \times 10^2 1.00210×102。
所以和是:
KaTeX parse error: Expected 'EOF', got '&' at position 24: … \times 2^{-4} &̲ = & 0.0001000_…
浮点乘法
步骤
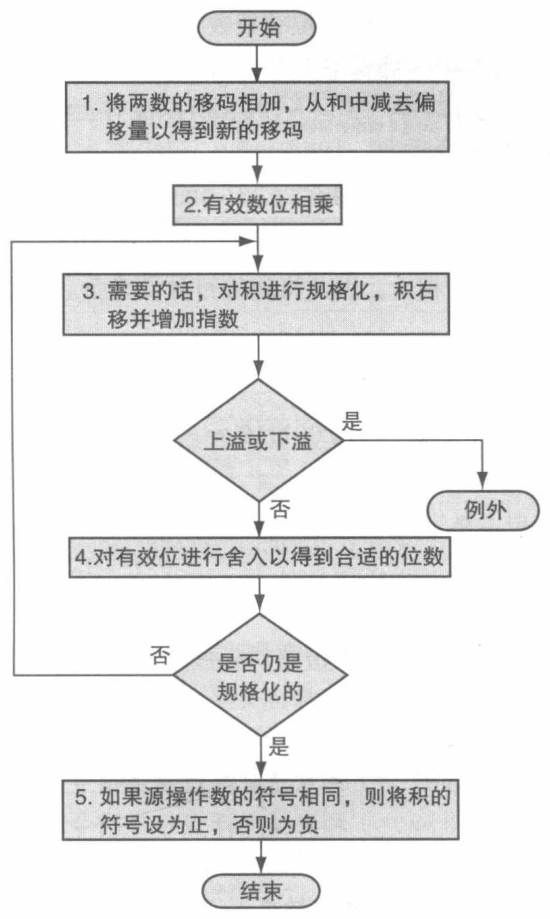
例子 —— 求 0.5 和 -0.4375 的乘积,使用二进制。
KaTeX parse error: Expected 'EOF', got '&' at position 6: 0.5 &̲ = & 1.000_2 \t…
第一步:将两数移码相加。
第一种方式:不带偏移值,直接加。
−
1
+
(
−
2
)
=
−
3
-1 + (-2) = -3
−1+(−2)=−3
第二种方式:使用移码相加,移码表示。
(
−
1
+
127
)
+
(
−
2
+
127
)
−
127
=
(
−
1
−
2
)
+
(
127
+
127
−
127
)
=
−
3
+
127
=
124
(-1+127)+(-2+127)-127=(-1-2)+(127+127-127)=-3+127=124
(−1+127)+(−2+127)−127=(−1−2)+(127+127−127)=−3+127=124
第二步:有效数位相乘。

每个操作数小数点右侧有三位数字,因此乘积的小数点应该放在从右数第 6 位有效位前面:
1.11000
0
2
1.110000_2
1.1100002
但我们需要保留 4 位有效位:
1.11
0
2
1.110_2
1.1102
算上前面的指数,用二进制科学记数法表示就是:
1.11
0
2
×
2
−
3
1.110_2 \times 2^{-3}
1.1102×2−3
第三步:对结果规格化,然后检查已否溢出。
1.11 0 2 × 2 − 3 1.110_2 \times 2^{-3} 1.1102×2−3 已经是规格化的形式了,因此无需规格化。
− 3 -3 −3 符合单精度指数 − 126 < = − 3 < = 127 -126<=-3<=127 −126<=−3<=127,因此没有溢出。
第四步:因为操作数为“异号得负”,因此将乘积的符号设为负。
所以,乘积为:
KaTeX parse error: Expected 'EOF', got '&' at position 25: … \times 2^{-3} &̲ = & -0.001110_…
参考文献
- 移码
- 单精度浮点
- 双精度浮点
- IEEE 754






![[Java 进阶面试题] CAS 和 Synchronized 优化过程](https://img-blog.csdnimg.cn/2e801aa85df74f31ba85ab1273150b1d.png)