Leetcode 回溯详解

回溯法

回溯法有“通用解题法”之称，用它可以系统地搜索问题的所有解。回溯法是一个既带有系统性又带有跳跃性的搜索算法。

在包含问题的所有解的解空间树中，按照深度优先搜索(DFS)）的策略，从根结点出发深度探索解空间树。当探索到某一结点时，要先判断该结点是否包含问题的解，如果包含，就从该结点出发继续探索下去，如果该结点不包含问题的解，则逐层向其祖先结点回溯。（其实回溯法就是对隐式图的深度优先搜索算法）。

若用回溯法求问题的所有解时，要回溯到根，且根结点的所有可行的子树都要已被搜索遍才结束。而若使用回溯法求任一个解时，只要搜索到问题的一个解就可以结束。

DFS

解题步骤

针对所给问题，定义问题的解空间
确定易于搜索的解空间结构
以深度优先方式搜索解空间，并在搜索过程中用剪枝函数避免无效搜索

子集树与排列树

下面的两棵解空间树是回溯法解题时常遇到的两类典型的解空间树，子集树与排列树

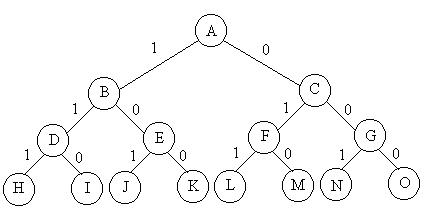
子集树

当所给问题是从n个元素的集合S中找出S满足某种性质的子集时，相应的解空间树称为子集树。例如从n个物品的0-1背包问题所相应的解空间树是一棵子集树，这类子集树通常有 ${2^n}$ 个叶结点，其结点总个数为 ${2 ^{n+1}- 1}$ 。遍历子集树的算法需O( ${2^n}$ )计算时间

用回溯法搜索子集树的一般算法可描述为：

/**
 * output(x)     记录或输出得到的可行解x
 * constraint(t) 当前结点的约束函数
 * bount(t)      当前结点的限界函数
 * @param t  t为当前解空间的层数
 */
void backtrack(int t){
	if(t >= n)
		output(x);
	else
		for (int i = 0; i <= 1; i++) {
			x[t] = i;
			if(constraint(t) && bount(t))
				backtrack(t+1);
		}
}

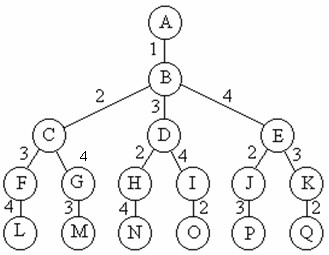
排列树

当所给问题是确定n个元素满足某种性质的排列时，相应的解空间树称为排列树。例如旅行售货员问题的解空间树是一棵排列树，这类排列树通常有 ${n!}$ 个叶结点。遍历子集树的算法需O( ${n!}$ )计算时间

用回溯法搜索排列树的一般算法可描述为：

/**
 * output(x)     记录或输出得到的可行解x
 * constraint(t) 当前结点的约束函数
 * bount(t)      当前结点的限界函数
 * @param t  t为当前解空间的层数
 */
void backtrack(int t){
	if(t >= n)
		output(x);
	else
		for (int i = t; i <= n; i++) {
			swap(x[t], x[i]);
			if(constraint(t) && bount(t))
				backtrack(t+1);
			swap(x[t], x[i]);
		}
}

Leetcode真题

电话号码的字母组合

解题思路：
经典排列树，按节点遍历

private String[] voc = new String[]{"","*", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
List<String> res = new ArrayList();
public List<String> letterCombinations(String digits) {
    if (digits == null || digits.length() == 0) {
        return res;
    }
    backtrack(digits, 0, new StringBuffer());
    return res;
}

public void backtrack(String digits, int index, StringBuffer s) {
    if (index == digits.length()) {
        res.add(s.toString());
        return;
    }
    int i = digits.charAt(index) - '0';
    for (char c : voc[i].toCharArray()) {
        s.append(c);
        backtrack(digits, index + 1, s);
        s.deleteCharAt(s.length() - 1);
    }
}

括号生成

解题思路：
排列树，按节点遍历

回溯结束条件：左括号数 = 右括号数 = 总数
左括号数<总数，字符串加入左括号
右括号数<总数且左括号数>右括号数，字符串加入右括号

List<String> res = new ArrayList<>();
public List<String> generateParenthesis(int n) {
    backtrack(n, 0, 0, "");
    return res;
}

void backtrack(int n, int l, int r, String str) {
    if (l == n && r == n) {
        res.add(str);
    }
    if (l < n) {
        backtrack(n, l + 1, r, str + "(");
    }
    if (r < n && l > r) {
        backtrack(n, l, r + 1, str + ")");
    }
}

N皇后

解题思路：
子集树，按节点遍历

回溯结束条件：所有层数放置完毕
每列循环遍历，当满足非冲突条件时(列，主对角线，副对角线不冲突)
放置该行的皇后
执行下一级回溯

两点位于同一对角线时，行列值相加/相减的值相等

List<List<String>> res = new ArrayList<>();
public List<List<String>> solveNQueens(int n) {
    if (n <= 0) {
        return res;
    }
    backtrack(0, n, new int[n]);
    return res;
}

/**
 * output(x)     记录或输出得到的可行解x
 * constraint(t) 当前结点的约束函数
 *
 * @param t      t为当前解空间的层数
 * @param n 总层数
 * @param queens 结果集，下标为行号，值为列号
 */
void backtrack(int t, int n, int[] queens) {
    if (t >= n) {
        output(res, n, queens);
        return;
    } else {
        for (int j = 0; j < n; j++) {
            if (constraint(t, j, n, queens)) {
                queens[t] = j;
                backtrack(t + 1, n, queens);
            }
        }
    }
}

/**
 * 检查是否存在冲突(列，主对角线，副对角线)
 * 两点位于同一对角线时，行列值相加/相减的值相等
 */
boolean constraint(int t, int j, int n, int[] queens) {
    for (int i = 0; i < t; i++) {
        if (queens[i] == j || i - queens[i] == t - j || i + queens[i] == t + j) {
            return false;
        }
    }
    return true;
}

void output(List<List<String>> res, int n, int[] queens) {
    List<String> list = new ArrayList<>();
    for (int i = 0; i < n; i++) {
        char[] chars = new char[n];
        Arrays.fill(chars, '.');
        chars[queens[i]] = 'Q';
        list.add(new String(chars));
    }
    res.add(list);
}