提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

何为贪心

1、顾名思义，贪心算法采用贪心的策略，保证每次操作都是局部最优的，从而使最
后得到的结果是全局最优的。
2、举一个最简单的例子：小明和小王喜欢吃苹果，小明可以吃五个，小王可以吃三个。已知苹果园里有吃不完的苹果，求小明和小王一共最多吃多少个苹果。在这个例子中，我们可以选用的贪心策略为，每个人吃自己能吃的最多数量的苹果，这在每个人身上都是局部最优的。又因为全局结果是局部结果的简单求和，且局部结果互不相干，因此局部最优的策略也同样是全局最优的策略。

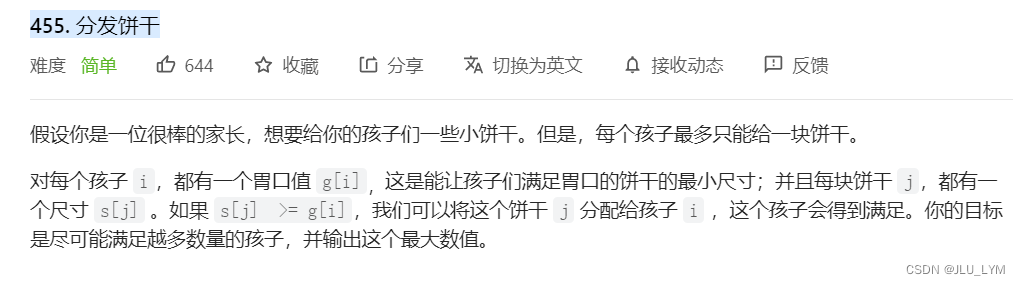
力扣455. 分发饼干

题目链接：455. 分发饼干

思路

1、明确本题目标：用手里的饼干，满足尽可能多的孩子
2、根据上面的目标，我们必须利用好手里的饼干，不能出现，孩子的胃口是1，有2/3/4大小的饼干，我们就要避免"浪费"，所以就要给孩子最接近他胃口的饼干
3、这样，每个人都可以获得最接近他胃口的饼干，都不会造成"浪费"，才能让更多的人得到饼干，这就是本题的贪心策略。

注意：
1、这种题，明显存在数组，并且我们解题需要使用到数组之中数字关系
2、但是，数组之中，是乱序，一定记住这个大原则：乱序会让时间复杂度最糟糕！
3、所以，第一步就是对两个数组进行排序
4、这样，从胃口最小的孩子入手，当前饼干连这个孩子都满足不了，则说明一定是无用饼干，就看下一个饼干去；若能满足，则一定是最优的。

代码

class Solution {
public:
	int findContentChildren(vector<int>& g, vector<int>& s) {
		sort(s.begin(), s.end());//排序
		sort(g.begin(), g.end());
		int i = 0, j = 0;//分别指向数组g s
		int g_size = g.size(), s_size = s.size();
		int ans = 0;//答案
		while (i < g_size&&j < s_size) {
			if (s[j] < g[i]) {//当前饼干连胃口最小的孩子都满足不了，一定不能满足任何一个孩子
				j++;
				continue;
			}
			else {//当前饼干一定是最适合当前胃口的孩子，并且之后的饼干一定大于了当前饼干造成了浪费，所以选后面的饼干会造成满足孩子的数量减少
				ans++;
				i++;
				j++;
			}
		}
		return ans;
	}
};