论文名称和地址：

Visualizing the Loss Landscape of Neural Nets

https://arxiv.org/pdf/1712.09913.pdf

1.1 背景和动机

作者主要想研究几个问题：

为什么我们能够最小化高度非凸神经损失函数？

为什么得到的最小值这个结果具有泛化性？

不同的神经网络网络架构如何影响损失函数分布 (loss landascape)，以及训练的超参数参数如何影响损失函数分布

1.2 损失函数可视化基础

一般通过最小化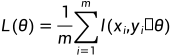 $\text{[math]}$ 来训练神经网络。其中, 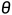$\text{[math]}$ 表示神经网络的参数, 函数 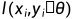$\text{[math]}$ 衡量神经网络对数据样本标签的预测程度, m 为数据样本的个数。神经网络包含许多参数, 因此它们的损失函数存在于一个非常高维的空间中。

一维的线性插值可视化方法

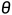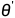一种已有的1维的可视化方法是线性插值法 (Linear interpolation), 就是选择两个参数向量 $\text{[math]}$ 和 $\text{[math]}$ , 并沿连接这两点的直线 $\text{[math]}$ 绘制损失函数的值 $\text{[math]}$ 。

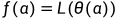但是一维线性插值方法有几个缺点。

一维线性插值方法去可视化神经网络的非凸性 (non-convexities) 是很困难的，这就导致了损失函数在最小化轨迹上似乎缺乏局部最小值。

一些损失函数具有非凸性，而这些非凸性与不同网络架构之间的泛化差异相关。

一维线性插值方法不考虑 Batch Normalization 或者网络中的不变性对称性。因此，由一维线性插值方法产生的插值结果可能具有误导性。

二维的线性插值可视化方法

为了使用二维的线性插值可视化方法, 我们可以在图中选择首先一个中心点 , 并选择两个方向向量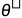 $\text{[math]}$ $\text{[math]}$ 和 $\text{[math]}$ 。

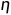然后, 在 1D (曲线) 情况下, 绘制一个形式为 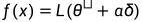$\text{[math]}$ 的函数, 或者在 2D (平面) 情况下, 绘制一个形式为 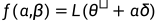$\text{[math]}$ 的函数。

以上方法的问题

虽然以上这两种在随机方向移动一个小距离，并绘制函数值的绘图方法很简单，但它无法捕捉损失函数的固有几何形状，并且不能用于比较两个不同的最小化器或两个不同的神经网络模型的几何形状。这是因为网络权重的比例不变性 (scale invariance) 。当使用 ReLU 非线性激活函数时，如果将网络中某一层的权重乘以10，并将下一层的权重除以10，网络输出将保持不变。当使用 BN 时，同理也存在这种不变性。

那么网络权重的比例不变性 (scale invariance) 对于以上的一维，二维的线性插值可视化方法有哪些影响呢？

——具有较大权重的神经网络可能具有平滑且缓慢变化的损失函数：比如说，如果权重的幅值比1大得多，那么将权重扰动一个单位对网络性能的影响很小。但是如果权重远小于1，那么同样的单位扰动可能会产生很大的影响，使损失函数对权重扰动显得相当敏感。

1.3 Filter Normalization

基于以上一维和二维的线性插值可视化方法的缺点，本文提出一种叫做 Filter Normalization 的可视化方法。这种方法的思想也是基于以上的一维，二维的线性插值可视化方法。

以上方法问题的核心其实就来自于 "单位扰动" ，即：

对于权重幅值较大的神经网络而言，一个单位的扰动对它没啥作用，即使得 loss 的改变几乎可以忽略不计，那么它就更可能具有一个平滑且缓慢变化的 loss landscape。

对于权重幅值较小的神经网络而言，一个单位的扰动对它会产生很大的影响，使得 loss 发生灾难性的改变，使得 loss landscape 对权重扰动显得相当敏感。

那么为了克服这个难题, 本文作者提出一种滤波器归一化 (Filter Normalization) 的做法, 即：对于网络权重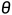 $\text{[math]}$ , 和一个随机的高斯方向向量d , 然后作者将d 中的每个滤波器归一化, 使其具有与 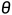$\text{[math]}$ 中相应滤波器相同的范数。换句话说, 进行替换, 如下式所示：

$\text{[math]}$

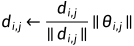
式中, d_{i,j} 代表第i 层, 第j 个滤波器的高斯方向向量, 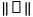$\text{[math]}$ 代表 Frobenius 范数。滤波器归一化 (Filter Normalization) 并不局限于卷积 (Conv) 层, 也适用于全连接（FC）层 (相当于 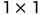$\text{[math]}$ 卷积)。

作者在下一节证明了经过滤波器归一化的图的锐度与泛化误差有很好的相关性，而没有滤波器归一化的图可能非常具有误导性。

1.4 可视化实验

Loss landscape 尖锐，扁平的困境

在上一节中，我们提到有的神经网络具有平滑且缓慢变化的 loss landscape (称为 sharp minimizer)，而有的具有剧烈变化的 loss landscape (称为 flat minimizer)。在本节中，将通过一些实验结果阐明：sharp minimizer 和 flat minimizer 的泛化性有什么关系？

在这里呢，作者探讨了 sharp minimizer 和 flat minimizer 的区别。

作者表明：使用传统的一维线性插值方法得到的结论是：sharp minimizer 和 flat minimizer 的泛化性没什么关系

曲线的锐度与模型的泛化性之间很好地相关。大 Batch Size 产生视觉上更尖锐的最小值 (尽管不是很明显)，但测试误差更高。

不同 Batch Size 使用滤波器归一化 1D 和 2D 的可视化结果

1.5 一些 Loss Surfaces 非凸结构的发现

大量经验表明，似乎有些神经结构比其他的更容易最小化。例如，使用 Skip Connection，ResNet 使得我们可以训练非常深的神经网络结构，而没有 Skip Connection 的相同的神经网络结构是不可训练的。而且，一个网络是否可以得到良好的训练很大程度上取决于训练开始时的初始参数。

作者使用可视化方法，对神经结构进行了实证研究，以探索为什么损失函数的非凸性在某些情况下似乎是有问题的

模型深度的影响

如下图所示，可以看到，当不使用残差连接时，网络深度对神经网络的 loss landscape 有显著的影响。比如当深度为20时，不使用残差连接的 ResNet-20-NS 有较好的表现，这并不太令人惊讶，因为用于 ImageNet 的原始VGG 网络有19层，也可以有效地训练。但是，随着网络深度的增加，VGG 类网络的损失面自发地从 (近) 凸过渡到混沌。ResNet-56-NS 具有显著的非凸性和大区域，其中梯度方向 (与图中描绘的等高线正常) 不指向中心的最小值。而且，随着向某些方向移动，损失函数会变得非常大。ResNet-110-NS 显示出更明显的非凸性，当我们在图中所示的各个方向移动时，它变得非常陡峭。

图中的对比很强烈——当神经网络比较浅时，不使用快捷连接（shortcut connection）对于损失分布的影响还不算大，即上图中的（a）和（d）图。

当网络达到了 56 层的深度时，无快捷连接（shortcut connection）的模型的等高线图中显示的损失函数基本是混乱的（图（e））。特别是在一些区域中，沿着梯度的方向运动并不能达到损失更小的区域。

这显然是很危险的，意味着梯度下降方法的效率被大大损害了；同时也从另一方面解释了模型的训练性，即为何有些模型的训练更容易，或者对于同一模型为何超参数的取值不同会对模型表现造成巨大影响。

假如模型初始化后落入了一个高度非凸的区域中，在整个训练过程中算法可能都无法找到一个比较好的解，因为梯度所指向的方向根本毫无意义。上图第三栏中，ResNet-110-noshort 显示了更极端的非凸性，不管向哪一个方向移动梯度都非常大。

我们特别需要注意的是在上图第一行中——即有快捷连接（shortcut connection）的 ResNet——即使模型的深度大大增加，中心的极小值的深度也并没有增加多少，即模型收敛的区域仍然是相对平坦的。而第二行中当我们去掉了 ResNet 的快捷连接（shortcut connection）时，图像中心紫线所代表的极小值的深度大大增加了。这样一个最直接的影响——上文已经提到——就是训练难度增加了。

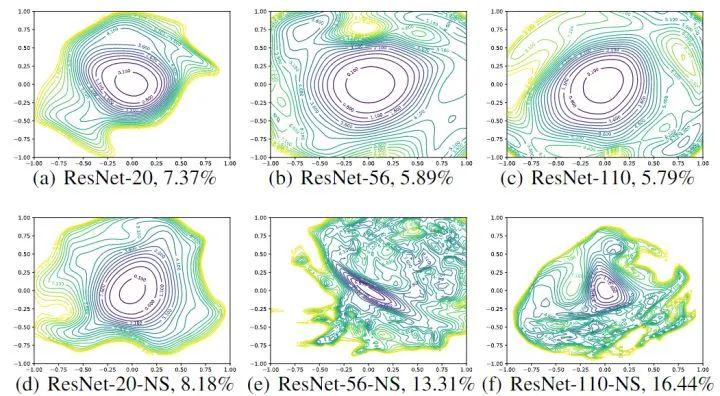
图3：Wide-ResNet-56 有残差连接 (上) 和无残差连接 (下) 的 loss landscape，k=2 意思是每层滤波器数量乘以2

有无残差连接的影响

残差连接对损失函数的 loss landscape 有显著的影响。在上图3中可以看到，随着深度的增加，残差连接阻止了向混沌行为的过渡。残差连接的影响似乎对深的网络架构最为重要。对于更浅的网络 (ResNet-20 和 ResNet-20-NS)，残差连接的影响不明显。如下图4所示是 ResNet-56 有无残差连接的 loss landscape 对比，图5所示是 ResNet-110 无残差连接和 DenseNet 121 层的 loss landscape 对比。

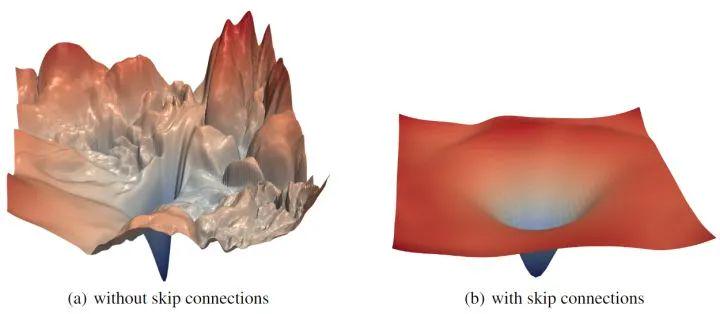
图4：ResNet-56 有无残差连接的 loss landscape 对比

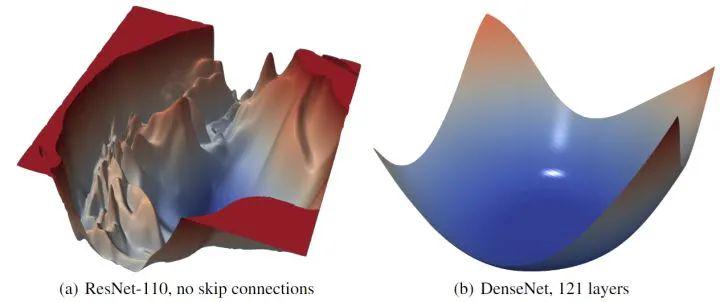
图5：ResNet-110 无残差连接和 DenseNet 121 层的 loss landscape 对比

模型宽度的影响

另一个比较有意思的发现在于，当神经网络的宽度增加——即每层的神经元个数增加——损失函数的曲面也变得更平滑了。这里作者使用了 RestNet 56 层的结构，仍然是第一行有快捷连接（shortcut connection），第二行无。其中每个子图下面的 k 表示隐藏神经元的倍数，即 k=2 为模型的宽度是 k=1 的模型的二倍。旁边的百分比数字表示模型的错误率。

可以看到更宽的模型的 loss landscape 更宽，即：增大网络宽度可以获得更宽更平坦的 loss landscape。

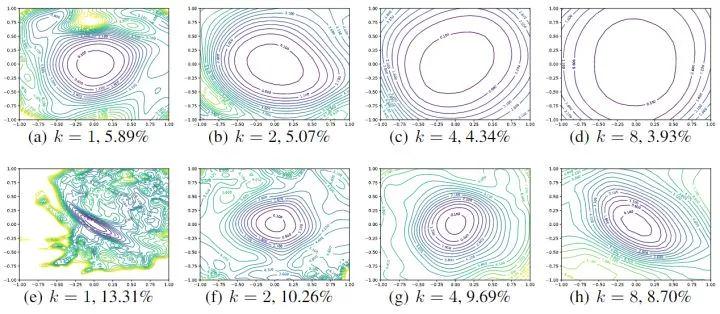
图6. Wide-ResNet-56 有残差连接 (上) 和无残差连接 (下) 的 loss landscape，k=2 意思是每层滤波器数量乘以2

[图片来源：Hao, L. et al. (2018). Visualizing the loss landscape of neural nets. NIPS.]

我们首先从上到下两两对比地讨论这些结果，可以看到有快捷连接（shortcut connection）总是比无快捷连接（shortcut connection）的损失函数曲面更平滑一些，极小值的位置也更浅。不过更重要的是当我们从左到右的进行分析时——随着模型宽度的增加，模型的损失曲面显著地变得更平缓了，也就是更浅了。

对于没有快捷连接（shortcut connection）的模型来说，增加模型宽度也许不能直接解决损失函数的分布中存在梯度混乱的问题，图（f）的四角都可以看到有很不平滑的等高线，但由于曲面变得更浅，我们可以侧面缓解这个问题。