Diffusion过程解析

前向和后向相互独立，前向过程使用马尔科夫链实现，反向过程采用神经网络进行预测。

前向过程

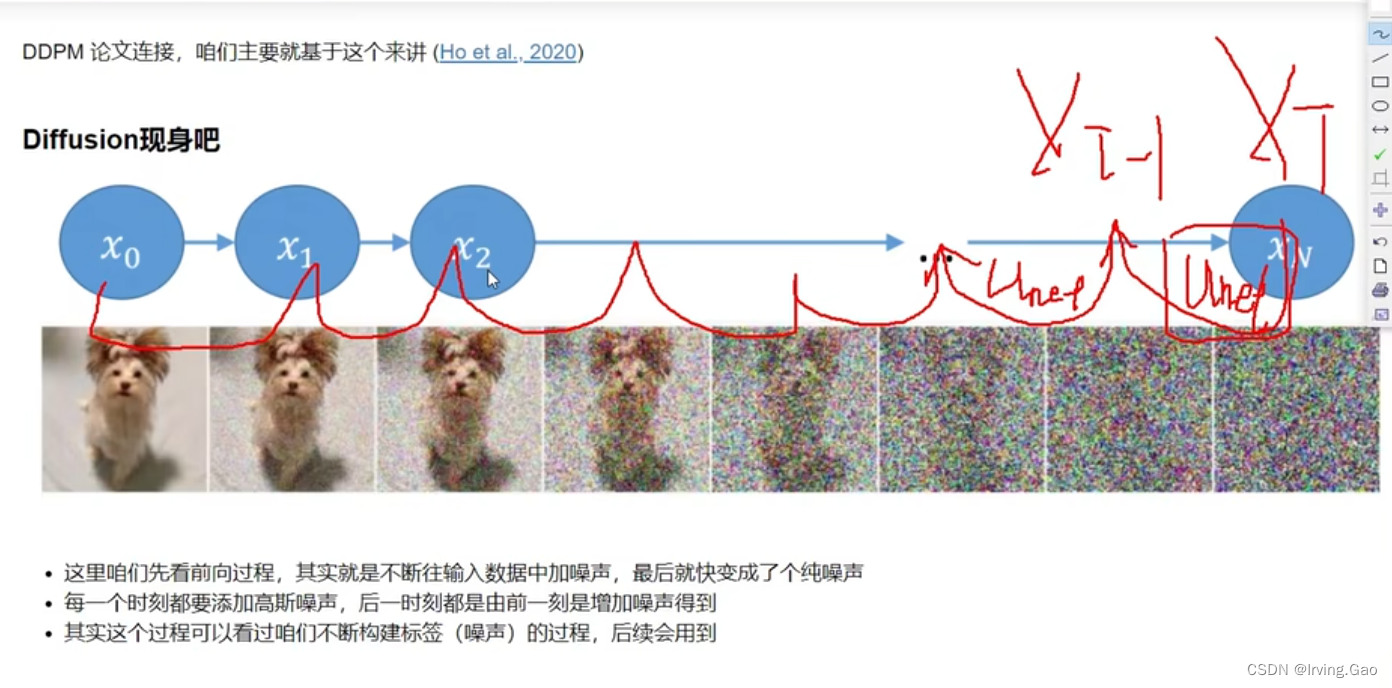
• 输入一个原始图片；
• 每一步添加噪声，噪声服从高斯分布（均值为0，方差为1，记作$N(0,1)$，服从正态分布）；
• 最终得到一个只含有噪声的图像；

公式详解

每一步增加噪声的求解

$$X_t=\sqrt{a_t}{X}_{t-1}+\sqrt{1-a_t}{\epsilon }_t$$

• $X_t$是当前时刻的图像；$X_{t-1}$是前一时刻的图像；
• $a_t$是噪声权重，随着 $t$ 的增加不断变化（论文中是从0.0001到0.02）；
• ${\epsilon }_t$是指每个时刻添加的独立的高斯噪声。

从起始状态到最终状态的公式

反向过程

反向过程是通过参数化的U-Net+Attention神经网络实现从噪声图像到原始图像的denoise。

损失函数

最小化该公式：

$$\Vert {\bar{z}}_t-z_{\theta }\left(\sqrt{{\bar{\alpha }}_t}{x}_0+\sqrt{1-{\bar{\alpha }}_t}{\bar{z}}_t,t\right)\Vert$$

• ${\bar{z}}_t$为 $t$ 时刻的噪声真值；
• $z_{\theta }$为噪声预测值；
• ${\bar{\alpha }}_t$为噪声参数，和 $t$ 有关；

总结公式

参考资料：

• 视频讲解：Diffusion Model：比“GAN"还要牛逼的图像生成模型！公式推导+论文精读，迪哥打你从零详解扩散模型！

代码资料

链接：https://pan.baidu.com/s/1P1WTZtr5UBLu9FVDXCk3nA?pwd=tuh4
提取码：tuh4

• 文字原理详解：由浅入深了解Diffusion Model
• 代码：https://github.com/zoubohao/DenoisingDiffusionProbabilityModel-ddpm-