01- 机器学习经典流程 (中国人寿保费项目) (项目一)

news2024/9/28 15:31:24

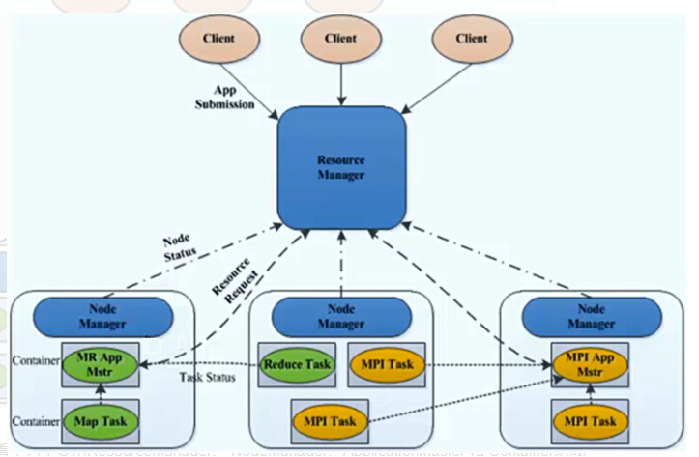
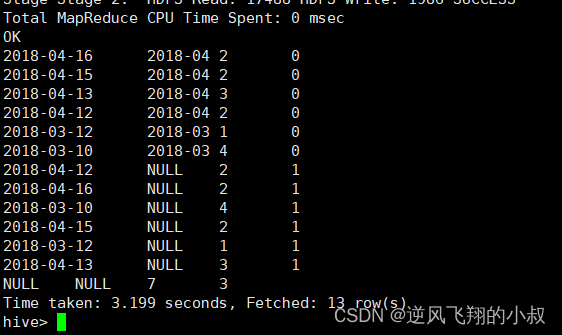
删除特征: data = data.drop(['region', 'sex'], axis=1)
特征数据调整: data.apply( )

# 体重指数，离散化转换，体重两种情况：标准、肥胖
def convert(df,bmi):
    df['bmi'] = 'fat' if df['bmi'] >= bmi else 'standard'
    return df
data = data.apply(convert, axis = 1, args=(30,))  # args 是传参

将非数字类型特征转换为数值: data = pd.get_dummies(data)
设定目标值和特征值:

X = data.drop('charges', axis=1) # 训练数据
y = data['charges'] # 目标值

中国人寿保费项目

数据存储: https://blog.csdn.net/March_A/article/details/128985290

1. 导入数据

import numpy as np
import pandas as pd
data = pd.read_excel('./中国人寿.xlsx')
data.head(10)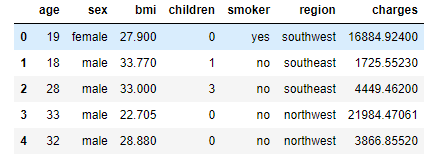

2. 查看数据特征

import seaborn as sns
# 性别对保费影响
sns.kdeplot(data['charges'],shade = True,hue = data['sex'])

# 地区对保费影响
sns.kdeplot(data['charges'],shade = True,hue = data['region'])

# 吸烟对保费影响
sns.kdeplot(data['charges'],shade = True,hue = data['smoker'])

# 孩子数量对保费影响
sns.kdeplot(data['charges'],shade = True,hue = data['children'],palette='Set1')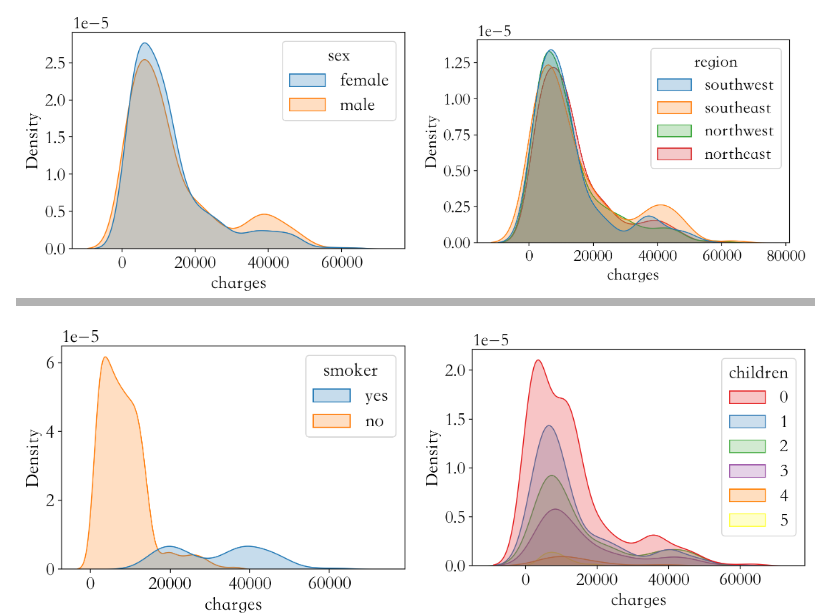

不同性别对保费影响不大，不同性别的保费的概率分布曲线基本重合，因此这个特征无足轻重，可以删除, 地区同理
吸烟与否对保费的概率分布曲线差别很大，整体来说不吸烟更加健康，那么保费就低，这个特征很重要
家庭孩子数量对保费有一定影响

3. 删除不重要数据

data = data.drop(['region', 'sex'], axis=1)

4 特征属性调整

# 体重指数，离散化转换，体重两种情况：标准、肥胖
def convert(df,bmi):
    df['bmi'] = 'fat' if df['bmi'] >= bmi else 'standard'
    return df
data = data.apply(convert, axis = 1, args=(30,))  # args 是传参
data.head()

5 非数值转换为数据类型 (去字符串)

# 特征提取，离散型数据转换为数值型数据
data = pd.get_dummies(data)
data.head()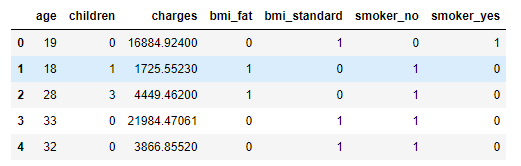

6 设定目标值和特征值

# 特征和目标值抽取
X = data.drop('charges', axis=1) # 训练数据
y = data['charges'] # 目标值
X.head()

7 数据拆分

# 数据拆分
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

8 数据升维

# 特征升维
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree= 2, include_bias = False)
X_train_poly = poly.fit_transform(X_train)
X_test_poly = poly.fit_transform(X_test)

9 模型训练

# 模型训练
from sklearn.linear_model import LinearRegression
model_1 = LinearRegression()
model_1.fit(X_train_poly, y_train)

# 使用弹性网络训练
from sklearn.linear_model import ElasticNet
model_2 = ElasticNet(alpha = 0.3,l1_ratio = 0.5,max_iter = 50000)
model_2.fit(X_train_poly,y_train)

10 模型评估

model_1.score(X_train_poly, y_train)  # 0.8624083431844988
model_2.score(X_test_poly, model_2.predict(X_test_poly))   # 1.0

# 模型评估
from sklearn.metrics import mean_squared_error,mean_squared_log_error
print('训练数据均方误差：',
      np.sqrt(mean_squared_error(y_train,model_1.predict(X_train_poly))))
print('测试数据均方误差：',
      np.sqrt(mean_squared_error(y_test,model_1.predict(X_test_poly))))

print('训练数据对数误差：',
      np.sqrt(mean_squared_log_error(y_train,model_1.predict(X_train_poly))))
print('测试数据对数误差：',
      np.sqrt(mean_squared_log_error(y_test,model_1.predict(X_test_poly))))

结论：