从0开始的秋招刷题路,记录下所刷每道题的题解,帮助自己回顾总结
50. Pow(x, n)
实现 pow(x, n) ,即计算 x 的整数 n 次幂函数(即,xn )。
示例 1:
输入:x = 2.00000, n = 10
输出:1024.00000
示例 2:
输入:x = 2.10000, n = 3
输出:9.26100
示例 3:
输入:x = 2.00000, n = -2
输出:0.25000
解释:2-2 = 1/22 = 1/4 = 0.25
提示:
-100.0 < x < 100.0
−
2
3
1
-2^31
−231 <= n <=
2
3
1
−
1
2^31-1
231−1
n 是一个整数
−
1
0
4
-10^4
−104 <= xn <=
1
0
4
10^4
104
解题思路1
直接模拟,有多少个n就执行多少次循环,不断与n进行相乘/相除
具体代码如下
代码1
class Solution {
public double myPow(double x, int n) {
if(x==0) return 0;
if(x==1 || n==0) return 1.0;
double res=1;
if(n>0) {
while (n!=0) {
res*=x;
n--;
}
}else {
while (n!=0) {
res/=x;
n++;
}
}
return res;
}
}
解题思路2
先举个例子,假设x=2,n=20,res为最终返回结果,算法的执行顺序如下:

如果根据代码1,则需要执行20次循环,如果执行代码2,则只需要执行5次循环;
如果n=1000,该算法只需要执行14次循环,这样大大减少了时间的消耗
具体代码如下:
代码2
class Solution {
public double myPow(double x, int n) {
if(x==0) return 0;
if(x==1 || n==0) return 1.0;
double res=1;
if(n>0) {
while (n!=0) {
if(n%2==0) {
x*=x;
n=n>>1;//n>>1等价于n/2
}
res*=x;
n--;
}
}else {
while (n!=0) {
if(n%2==0) {
x*=x;
n=n>>1;//n>>1等价于n/2
}
res/=x;
n++;
}
}
return res;
}
}
/**
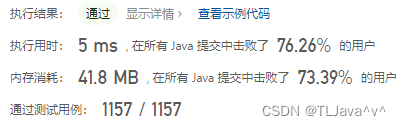
执行用时:0 ms, 在所有 Java 提交中击败了100.00%的用户
内存消耗:40.3 MB, 在所有 Java 提交中击败了13.54%的用户