【状态估计】基于二进制粒子群优化（BPSO）求解最佳 PMU优化配置研究【IEEE30、39、57、118节点】（Matlab代码实现）

news2024/9/28 17:35:24

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

近年来，随着大量分布式电源（distributed generation）接入配电网，使配电网朝着更加灵活的方向发展，配电网管理模式从被动向主动转变[1] 。状态估计是通过建立适当的网络模型对配电网进行在线监测和分析的功能。随着分布式能源集成对系统建模和运行的影响越来越大，对配电系统状态估计要求也越来越严格[2] 。目前，电力系统大多数据来源于数据采集与监控（SCADA）系统，但该系统量测数据采集周期较长，无法得到电网中的实时数据。虽然同步相量量测单元能够提供高精度的实时量测数据来提高状态估计精度[3] ，但由于成本和技术的限制，我国配电网安装的 PMU 装置数量有限，得到的实时量测数据较少。状态估计作为配电管理系统不可或缺的组成要素，其主要研究内容是如何在有限数量的 PMU 量测装置情况下尽可能地提高配电网状态估计精度。国内外已有大量学者针对最优 PMU 装置（optimal PMU placement，OPP）进行了大量的研究[4-9] 。目前，PMU 量测装置的优化目标主要分为满足系统可观性（拓扑可观和数值可观）

[10-12] 和提高状态估计精度[13-15] 两大类，解决这两类问题的对应优化算法有数值优化算法和启发式优化算法。数值优化算法主要分为穷举法和整数规划法，虽然整数规划法发展较为成熟，但配电网节点数目较多，短时间不可能大规模安装 PMU 量测装置，所以整数规划法不满足系统可观性的要求。文献[16]从不可观测度优化的角度出发，利用整数规划模型求解，在误差最大的节点装置 PMU，但没有考虑到配电网系统中节点较多而零注入节点较少的情况。启发式算法的全局搜索能力强，适用于非线性、高维度的模型求解问题。本文基于二进制粒子群优化（BPSO）求解最佳 PMU优化配置研究。

📚2 运行结果

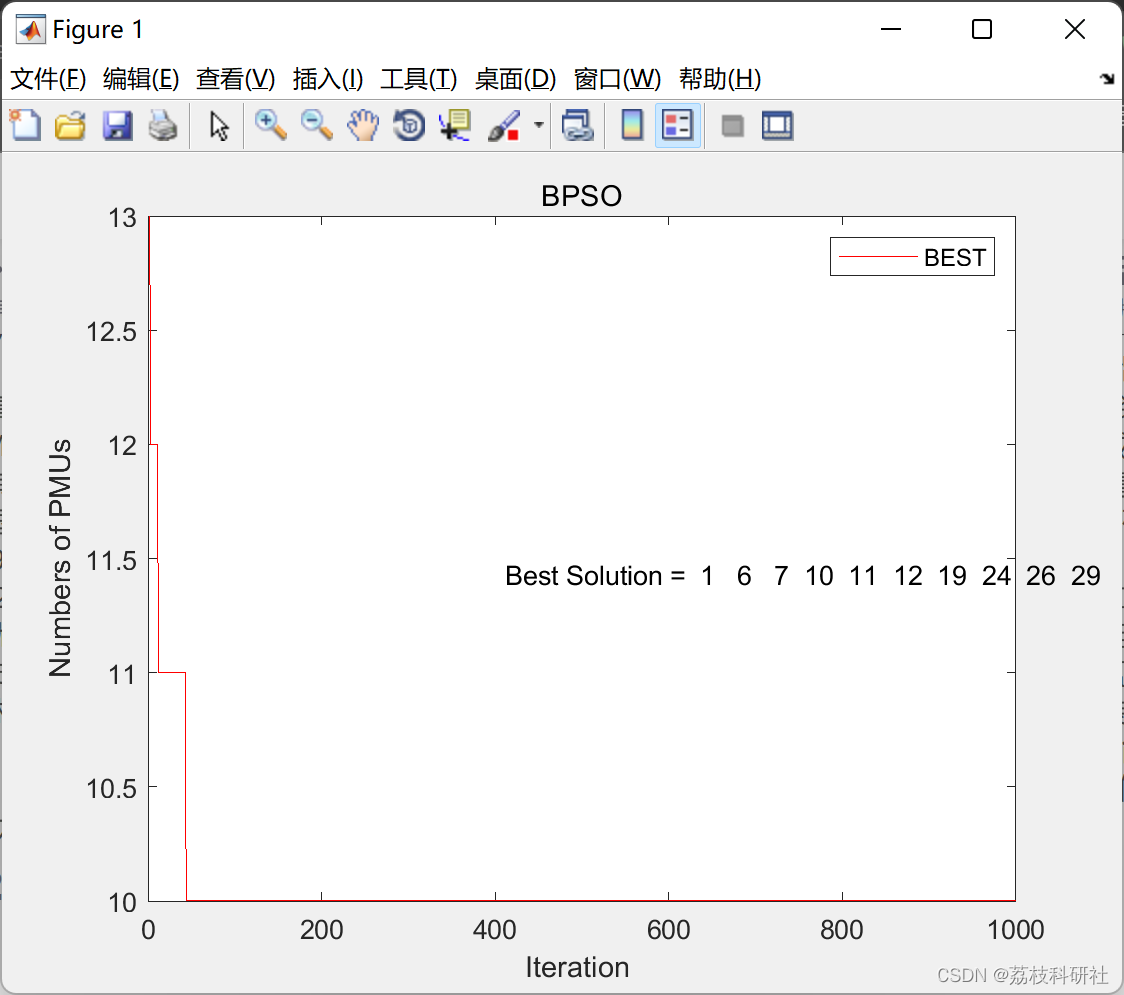
主函数代码：

clc
clear
close all
format shortG
commandwindow;

%% parameters setting

nvar=30; % number of variable
lb=0*ones(1,nvar); % lower bound
ub=1*ones(1,nvar); % upper bound

popsize=1000; % population size
maxiter=1000; % max of iteation

c1=1;
c2=1;

damp=1;

%% initial population algorithm

tic
emp.var=[];
emp.fit=[];
emp.vel=[];

par=repmat(emp,popsize,1);

for i=1:popsize

par(i).vel=lb+rand(1,nvar).*(ub-lb);
R=rand(1,nvar);
par(i).var=R>(1./(1+exp(-par(i).vel)));
par(i).fit=IEEE_30_Bus(par(i).var);

end

bpar=par;
[value,index]=min([par.fit]);
gpar=par(index);

%% main loop algorithm

BEST=zeros(maxiter,1);

for iter=1:maxiter

for i=1:popsize

par(i).vel=par(i).vel-...
c1*rand(1,nvar).*(bpar(i).var-par(i).var)-...
c2*rand(1,nvar).*(gpar.var-par(i).var);

par(i).vel=par(i).vel*damp;


par(i).vel=min(par(i).vel,ub);
par(i).vel=max(par(i).vel,lb);


R=rand(1,nvar);

par(i).var=R>(1./(1+exp(-par(i).vel)));

par(i).fit=IEEE_30_Bus(par(i).var);


if par(i).fit<bpar(i).fit
bpar(i)=par(i);

if bpar(i).fit<gpar.fit
gpar=bpar(i);
end
end

end

BEST(iter)=gpar.fit;

disp([ ' Iter = ' num2str(iter) ' BEST = ' num2str(BEST(iter)) ])

end

%% results algorithm

disp([ ' Best Solution = ' num2str(find(gpar.var==1))]);
disp([ ' Best Fitness = ' num2str(gpar.fit)]);
disp([ ' Time = ' num2str(toc)]);

figure(1);
plot(BEST,'r');
xlabel('Iteration ');
ylabel(' Numbers of PMUs ');
legend('BEST');
title('BPSO');
gtext([' Best Solution = ' num2str(find(gpar.var==1)) ' Best Fitness = ' num2str(gpar.fit) ] );