一、判断子序列

题目描述：

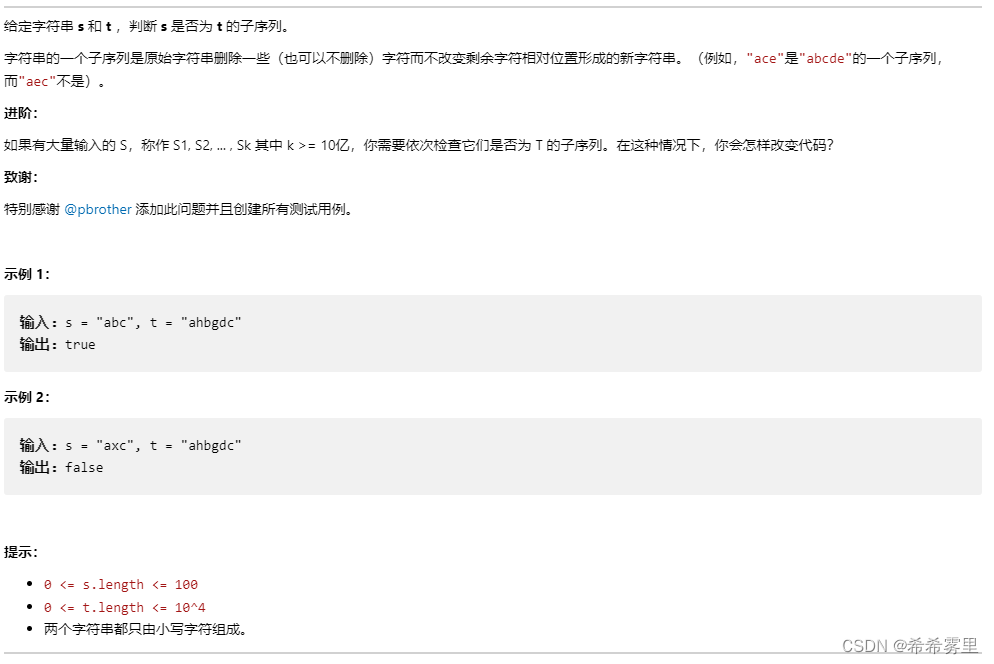
 思路和想法：

        这道题目还是最长公共子序列的拓展，只是这里进行删除的一定是t字符串，当不相等时，dp[i][j] = dp[i][j - 1]；其余基本一致。当最长公共子序列个数等s.size()时，返回true；● 1143.最长公共子序列 

#include<string>
#include<vector>
using namespace std;

class Solution {
public:
    bool isSubsequence(string s, string t) {
        if(s.size() == 0) return true;
        if(s.size() > t.size()) return false;
        vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1,0));

        for (int i = 1; i <= s.size(); i++)
        {
            for (int j = 1; j <= t.size(); j++)
            {
                if(s[i - 1] == t[j - 1]) 
                {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }else{
                    //删除元素一定是t字符串
                    dp[i][j] = dp[i][j - 1];
                }
                if(dp[i][j] == s.size()) return true;
            }
        }
        return false;
        
    }
};

二、不同的子序列

题目描述：

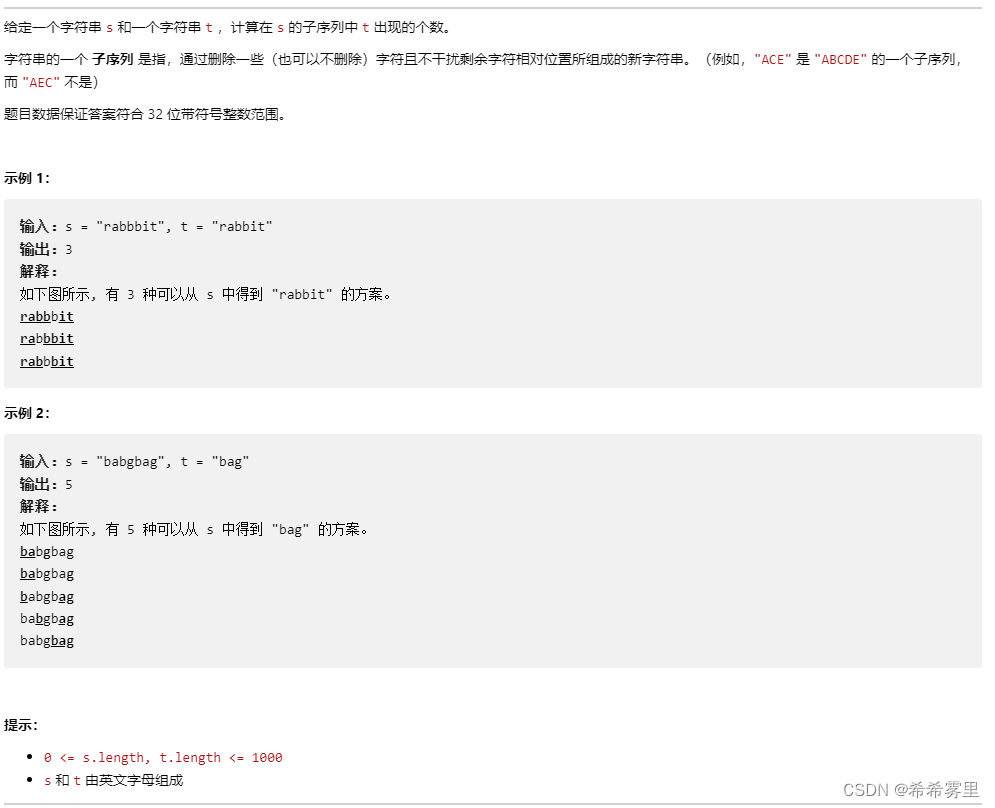
思路和想法：

（1）dp[i][j] : 以i - 1为结尾的s中有j - 1为尾的t的个数。

（2）当（s[i - 1] == j[i - 1]）时，dp[i][j] = dp[i  - 1][j  - 1] + dp[i - 1][j];当（s[i - 1] != j[i - 1]）时,dp[i][j] = dp[i - 1][j]。

这里要注意dp数组的定义：

（1）vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1,0));会出现溢出的情况

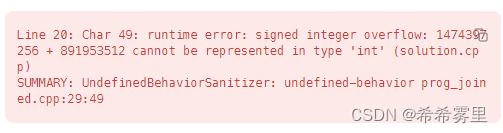
（2） vector<vector<uint64_t>> dp(s.size() + 1, vector<uint64_t>(t.size() + 1,0));

#include<vector>
#include<string>
using namespace std;

class Solution {
public:
    int numDistinct(string s, string t) {
        if(s.size() < t.size()) return 0;
        vector<vector<uint64_t>> dp(s.size() + 1, vector<uint64_t>(t.size() + 1,0));
        //第一行和第一列初始化
        for (int i = 0; i < s.size(); i++) dp[i][0] = 1;  
        for (int j = 1; j < t.size(); j++) dp[0][j] = 0;          

        for (int i = 1; i <= s.size(); i++)
        {
            for (int j = 1; j <= t.size(); j++)
            {
                if(s[i - 1] == t[j - 1]) 
                {
                    dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
                }else{
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        return dp[s.size()][t.size()];        
    }
};