堆：

堆是一颗完全二叉树，分为大根堆和小根堆两种。大根堆：根节点大于等于左右节点；小根堆：根节点小于等于左右节点。所以大根堆的根节点是最大值，小根堆的根节点是最小值。

c++中priority_queue可以用来声明堆：

大根堆：priority_queue<int,vector<int>,less<int>>q；

小根堆：priority_queue<int,vector<int>,greater<int>>q。

操作：

q.size()，返回堆中的元素个数；q.top()，返回堆顶元素；q.push(x)，插入元素x；q.pop()，删除堆顶。

手写堆：

完全二叉树有一个性质：我们假设根节点标号为1，那么每个点的左儿子等于它的下标乘2，右儿子等于它的下标乘2加1。所以我们可以用一个一维数组来模拟堆。

假设我们改变堆中的一个数，那么要使他依旧是一个堆的话，我们需要将其往上移动，或者将其往下移动。

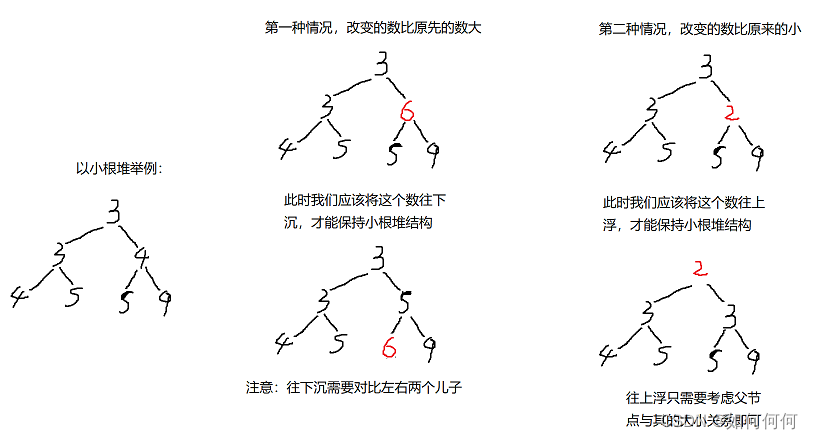
根据上浮和下沉这两个操作，我们可以对堆进行如下操作：

取出/删除堆顶：将堆中最后一个元素（数列中最后一个元素）覆盖到堆顶，然后下沉。

插入元素：向堆的最后面加入一个元素，然后上浮。

删除任意元素：将堆中最后一个元素覆盖到该位置，然后根据情况确定是上浮还是下沉。

如何将数组建成堆：

我们从最后一个非叶子节点开始，一直到根节点，每个节点执行一次下沉操作，就可以建成堆。对于一个节点个数是n，根节点下标是1的完全二叉树，第一个非叶子节点的下标是n/2（下取整），也就是说我们将n/2到1的节点一次进行down操作即可。

上浮操作和下沉操作如何完成：

下沉操作：

我们将要下沉的节点和其左右儿子对比，如果有儿子小于它，这说明他需要down，则我们将其和最小的儿子交换，然后递归处理。

上浮操作：

给出两个操作的代码：

void down(int i)
{
    int t = i;
    if (i * 2 <= cnt && heap[i * 2] < heap[t])t = i * 2;
    if (i * 2 + 1 <= cnt && heap[i * 2 + 1] < heap[t])t = i * 2 + 1;
    if (heap[t] != heap[i]) {
        swap(heap[i], heap[t]);
        down(t);
    }
    return;
}


//不管是左儿子还是右儿子，除2向下取整都会得到根节点
void up(int i)
{
    int t = i;
    if (i / 2 >= 1 && heap[t] < heap[i / 2])t = i / 2;
    if (t != i) {
        swap(heap[t], heap[i]);
        up(t);
    }
    return;
}