wy的leetcode刷题记录_Day48

声明

本文章的所有题目信息都来源于leetcode
如有侵权请联系我删掉!
时间：2022-11-21

前言

补前几天的blog

808. 分汤

今天的每日一题是：808. 分汤

题目介绍

有 A 和 B 两种类型的汤。一开始每种类型的汤有 n 毫升。有四种分配操作：

提供 100ml 的汤A 和 0ml 的汤B 。
提供 75ml 的汤A 和 25ml 的汤B 。
提供 50ml 的汤A 和 50ml 的汤B 。
提供 25ml 的汤A 和 75ml 的汤B 。

当我们把汤分配给某人之后，汤就没有了。每个回合，我们将从四种概率同为 0.25 的操作中进行分配选择。如果汤的剩余量不足以完成某次操作，我们将尽可能分配。当两种类型的汤都分配完时，停止操作。

注意不存在先分配 100 ml 汤B 的操作。

需要返回的值：汤A 先分配完的概率 + 汤A和汤B 同时分配完的概率 / 2。返回值在正确答案 10-5 的范围内将被认为是正确的。

示例 1:
输入: n = 50
输出: 0.62500
解释:如果我们选择前两个操作，A 首先将变为空。对于第三个操作，A 和 B会同时变为空。对于第四个操作，B 首先将变为空。所以 A 变为空的总概率加上 A 和 B 同时变为空的概率的一半是 0.25 *(1 +1 + 0.5 + 0)= 0.625。

示例 2:
输入: n = 100
输出: 0.71875

思路

方法一：动态规划：
1、确定dp数组的含义：dp[i][j]表示A还剩下i份，B还剩下j份的概率值。
2、确定dp数组的递推公式：由题目可知可从四个方面推当前阶段，这里我们的顺序是从0向n份开始推，这也是由我们的递推公式所决定的，四个方面是

4份A+0份B
3份A+1份B
2份A+2份B
1份A+3份B

所以我们的递推公式就应该是：

                dp[i][j] = (dp[max(0, i - 4)][j] + dp[max(0, i - 3)][max(0, j - 1)] +dp[max(0, i - 2)][max(0, j - 2)] + dp[max(0, i - 1)][max(0, j - 3)]) / 4.0;//来自四个状态:4A+0B,3A+1B,2A+2B,1A+3B

这里我们用了max，是为了在i和j小于四份的时候表达出仍然按上面四个方面卖，但是可能货量不够但是要尽可能卖出去，也就是为负数了，而数组下标又没有负数所以我们使用max来时程序能够运行。

代码

dfs记忆化搜索：很像之前学的树遍历中的dfs不过这里遍历的方式相似不过规则不同而已，缺点是多次重复计算了dp和调用dfs，其实用一个数组去记录就可以了。

class Solution {
public:
    double soupServings(int n) {
        
        n = ceil((double) n / 25);
        if (n >= 179) {
            return 1.0;
        }
        vector<vector<double>> memory(n + 1, vector<double>(n + 1));
        return dfs(n, n, memory);
    }

    double dfs(int a, int b,vector<vector<double>> &memo) {
        if (a <= 0 && b <= 0) {
            return 0.5;
        } else if (a <= 0) {
            return 1;
        } else if (b <= 0) {
            return 0;
        }
        if (memo[a][b] > 0) {
            return memo[a][b];
        }
        memo[a][b] = 0.25 * (dfs(a - 4, b,memo) + dfs(a - 3, b - 1,memo) + 
                             dfs(a - 2, b - 2,memo) + dfs(a - 1, b - 3,memo));
        return memo[a][b];
    }

};

动态规划：相较于dfs的记忆化搜索省去了不少空间和时间

class Solution {
public:
    double soupServings(int n) {
        n = ceil((double) n / 25);//量化减小 变成分批 每25ml分成一批
        if(n>=179)//由于题目要求保留五位 经过计算后发现再批次大于179之后无限接近于1
            return 1;
        vector<vector<double>> dp(n+1,vector<double>(n+1));

        dp[0][0]=0.5;//0 0 表示A 和B同时分配完
        for(int i=1;i<=n;i++)
        {
            dp[0][i]=1.0;//A先被分配完 B仍由残留  
        }
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=n;j++)
            {
                dp[i][j] = (dp[max(0, i - 4)][j] + dp[max(0, i - 3)][max(0, j - 1)] +dp[max(0, i - 2)][max(0, j - 2)] + dp[max(0, i - 1)][max(0, j - 3)]) / 4.0;//来自四个状态:4A+0B,3A+1B,2A+2B,1A+3B
            }
        }
        return dp[n][n];

    }
};

收获

巩固了动态规划的知识，以及在处理递推时的一些小技巧。

654. 最大二叉树

题目介绍

给定一个不重复的整数数组 nums 。最大二叉树可以用下面的算法从 nums 递归地构建:

创建一个根节点，其值为 nums 中的最大值。
递归地在最大值左边的子数组前缀上构建左子树。
递归地在最大值右边的子数组后缀上构建右子树。

返回 nums 构建的最大二叉树。

示例 1：

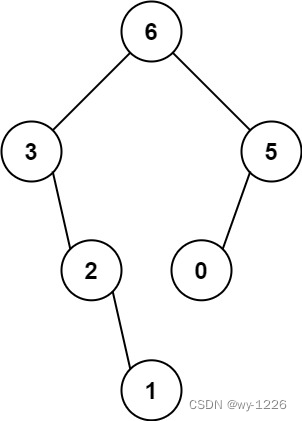
输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：

[3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
[3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
空数组，无子节点。
[2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
空数组，无子节点。
只有一个元素，所以子节点是一个值为 1 的节点。

[0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
只有一个元素，所以子节点是一个值为 0 的节点。
空数组，无子节点。示例 2：

示例 2：

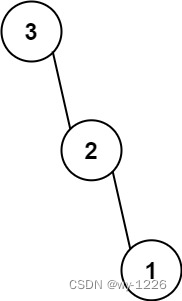
输入：nums = [3,2,1]
输出：[3,null,2,null,1]

思路

简单的模拟题，使用递归思路，根据题意找到数组中最大的值和其下标，并根据这个最大的值以此创建一个节点，根据这个下标分割数组将其分为左右俩部分，也就是左右子树，分别作为下一次迭代的输入参数。递归出口就是当数组大小为1的时候就是递归到叶子节点的时候直接将创建的节点返回就可以。

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        int n=nums.size();
        if(n==0)
            return nullptr;
        if(n==1)
            return new TreeNode(nums[0]);
        int maxVal=0;
        int maxIndex=0;
        for(int i=0;i<n;i++)
        {
            if(nums[i]>maxVal)
            {
                maxVal=nums[i];
                maxIndex=i;
            }
        }
        TreeNode* newNode=new TreeNode(maxVal);
        if(maxIndex>0)
        {
            vector<int> num_left(nums.begin(),nums.begin()+maxIndex);
            newNode->left=constructMaximumBinaryTree(num_left);
        }
        if(maxIndex<n-1)
        {
            vector<int> num_left(nums.begin()+maxIndex+1,nums.end());
            newNode->right=constructMaximumBinaryTree(num_left);
        }
        return newNode;
    }
};