最近流浪地球2，三体电视剧火得一塌糊涂，《三体》中罗辑用咒语标记了三体星系位置，利用黑暗森林理论与三体人对峙长达两百年，那么这种定位技术在现实中是否存在呢？

咒语标记三体星系位置这件事，听起来很玄乎但事实上是可以做到的，而且人类已经这么做过了

旅行者1号2号发射时携带了一张铜质镀金唱片，唱片的背面是这样的：

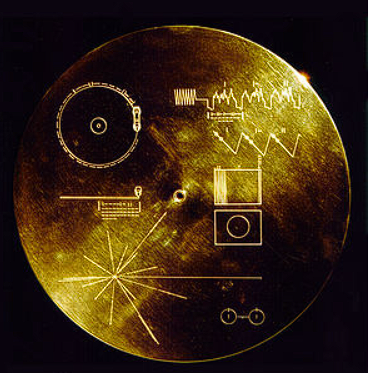
看到左下角的十多条发射线了吗？这代表着太阳相对于临近的14颗脉冲星以及银河系中心的相对位置和距离。脉冲星的脉冲周期直接以二进制的形式刻在了线上，如果将来有一天，高智慧的外星人发现了这张板，并且外星人的数据库里保存有银河系所有恒星的运动历史记录，那么他们就能容易地通过三角测算法发现，曾经有一颗恒星可以精确匹配这幅图里的位置，从而找到太阳系和太阳。外星人甚至可以通过脉冲周期，以及飞船上一块高纯度钚238的半衰期推算出飞船实际的发射时间距离他们发现它到底过了多久。

当然，更作死的是在旅行者号之前发射的先驱者10号11号携带的镀金铝板，它的样子是这样的：

不但标识了太阳系的位置，还把地球和先驱者探测器连了起来，一看就知道是从地球发射出去的，并且大大地画了人类男女的裸体长啥样。

一旦被有恶意的地外文明发现，后果不堪设想……

行星定位的原理

行星运动理论有很多种，遗憾的是国内并没有公开发表的系统的行星理论。因此，要想计算行星位置，只能使用国外的或历史上天文学家的天体运动理论进行计算。

目前，可供我们选择的方法分类如下：

1）直接利用开普勒行星三定律。此类方法属运动学范畴，可获0.01度的黄经精度；

开普勒第一定律：每一个行星都沿各自的椭圆轨道环绕太阳，而太阳则处在椭圆的一个焦点中。

开普勒第二定律：在相等时间内，太阳和运动着的行星的连线所扫过的面积都是相等的。

开普勒第三定律：各个行星绕太阳公转周期的平方及其椭圆轨道的半长轴的立方成正比。

2）拉普拉斯等牛顿的忠实信徒们，利用牛顿定律，结合适当的数学方法得到的行星位置的解析解，此类方法属动力学范畴，称为解析法；

3）运用牛顿定律，直接利用计算机进行数值积分得到超高精度的结果(现代方法)。比较著名的是美国国家航空航天局下属的喷气推进实验室的DE系列星历表。2005年以后的中国紫金山天文台出版的《中国天文年历》就是利用DE405星表推算的。

4）改良前人的解析法解法，使之适合计算机计算(现代方法)，此类方法常称为半解析法。这些方法的精度已经非常接近DE系列星历表。