一、前言

RANSAC(Random Sample Consensus)算法并不陌生，在上一篇博客中（基于SIFT的图像Matlab拼接教程）也提到过，之前代码中也多次用过，其在直(曲)线拟合、特征匹配、过滤外点(Outlier)等领域有着重要的应用。RANSAC出现的原因以及重要意义在于：虽然最小二乘可以十分有效地进行拟合，但其对离群点非常敏感，在离群点出现的情况下很有可能出现“一颗老鼠屎坏一锅汤”的情况。RANSAC就是为了解决这个问题而产生的。

二、介绍

正如其名字所说，RANSAC的核心思想是随机采样一致性，类似于投票：当有最多数据点符合某个模型时，即认为该模型是正确的，并且根据其算出的、误差在阈值内的数据点为内点。简单描述算法过程是：首先从数据点中随机选择指定数量的点构建模型，然后将全部数据点带入构建的模型中，若计算得到的结果与真实数据差异小于误差阈值，则认为其是内点，否则认为是外点。统计全部数据点中内点的个数并记录估计的模型参数。重复上述步骤一定次数，得到多个结果，选取内点数量最多时候对应的模型参数，即认为是正确的模型。根据这个模型计算出的误差在阈值内的所有点即为最终选择的内点。这样便完成了离群点的剔除。

RANSAC在实际使用中有几个常用的公式，整理如下：

选择某个点，其为内点的概率：

建立一个正确模型的概率，这里n表示建立一个模型所需要的样本点个数：

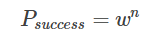
经过k次迭代后没有建立一个正确模型的概率：

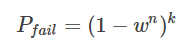
经过k次迭代后，建立一个正确模型的概率(成功率)：

期望RANSAC的成功率为p，最少迭代次数k：

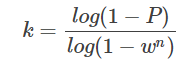
若建立模型需要m个点，数据集有n个数据，遍历一遍数据集需要的次数：

可以看到，在实际中第四和第五个式子最为常用。一个用来估计当前状态下成功的概率，另一个是估计最少迭代次数。这里需要注意的是公式5只是给出了最少应该迭代的次数，并不是说只能迭代这么多次。其实对于RANSAC算法，只要迭代次数足够多，最终肯定能得到最优的结果。只是从实际角度希望可以在最少迭代次数下最大概率获得最优结果，这便是公式5存在的意义。从理论上说迭代次数没有上限，而且由于RANSAC的机制：取所有迭代次数中效果最好的，所以迭代次数越多越有可能得到最好的结果。若遍历了一遍所有数据，则肯定能获得最好结果。但从实际应用的角度希望找到最合适的次数，公式5和公式6一个给出了迭代次数下限，一个给出了迭代次数上限。若小于下限，则有非常大可能得不到最优结果；如果超过上限太多，则会增加冗余计算量，意义不大。

通过以上的介绍，需要注意以下几点：

• RANSAC并不是一个“死板的”算法，而是一种思想。正是这种思想使其非常灵活，具体实现形式也可能千差万别。这里活就活在模型与误差评价指标。

• RANSAC的内点选取是与模型估计紧密耦合的。

• 误差阈值ε是项“技术活”。它一方面决定了估计模型的精度，另一方面决定了最终选取的内点个数。

• 并非所有数据都适合用RANSAC去除外点，它适用与遵循某种分布规律、可用模型拟合的数据

• RANSAC每次迭代的结果并不一定是更好的、进化的。因为是随机采样，所以每次迭代的结果也是随机的。不断增加的是我们获得最优模型和内点的概率。

三、RANSAC实例应用

3.1RANSAC拟合直线

首先可以使用最小二乘进行直线拟合，具体是利用SVD对系数矩阵A进行分解，取V的最右边一列为结果。拟合结果如下：

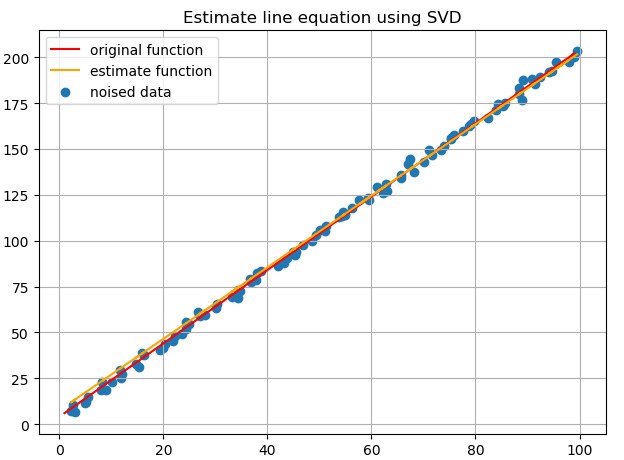
正如上文所说，最小二乘对于离群点非常敏感，下面动图演示了这一过程：

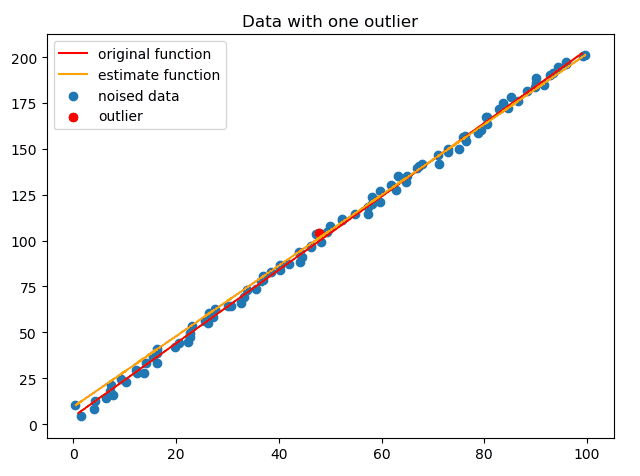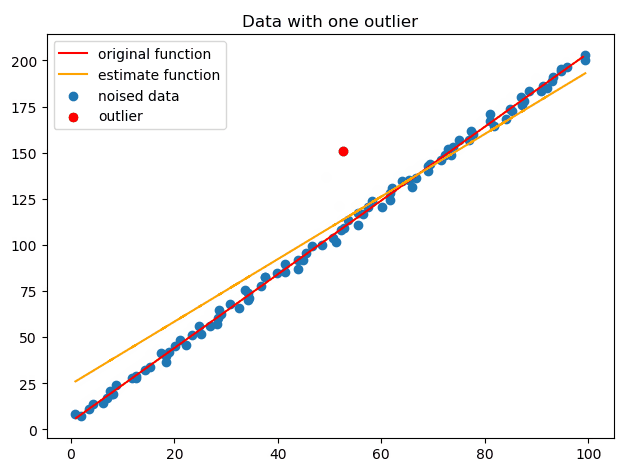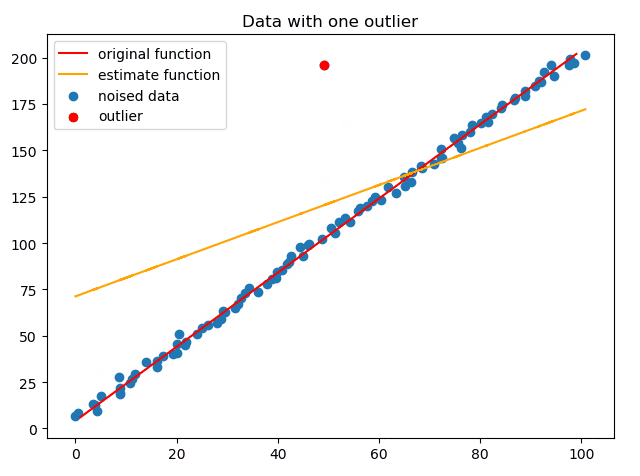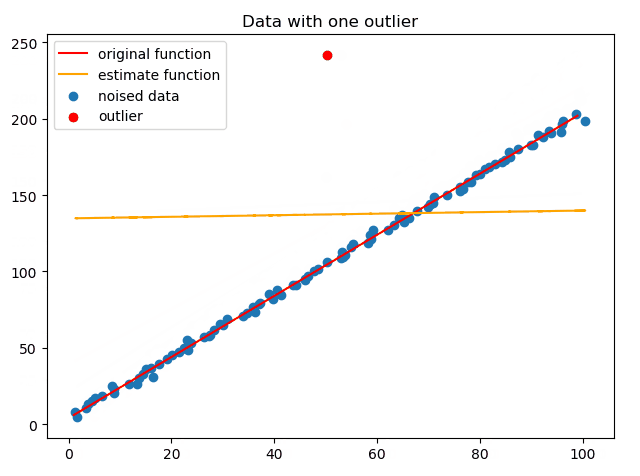
因此，为了能在有离群点的情况下拟合出直线，使用RANSAC算法，如下动图演示了RANSAC不断迭代的过程：

这里重要的就是误差定义，定义误差为某点到直线的垂直距离而不是Δx、Δy。

3.2RANSAC求解单应矩阵

下图为SVD进行单应矩阵估计：

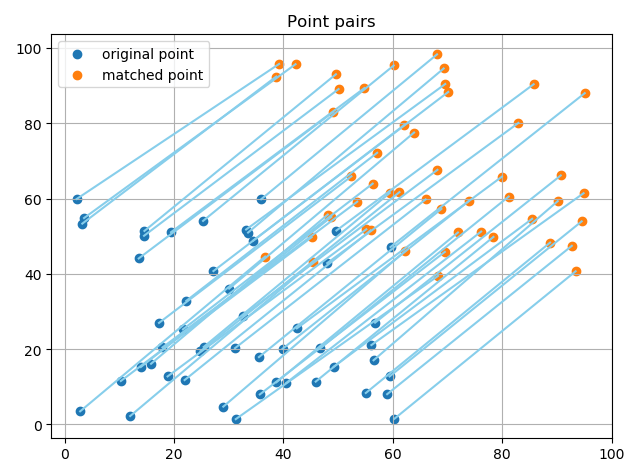
可以很明显地发现，如果不去除离群点会对最终估计结果有非常大的影响。所以用RANSAC算法进行剔除，动图如下：

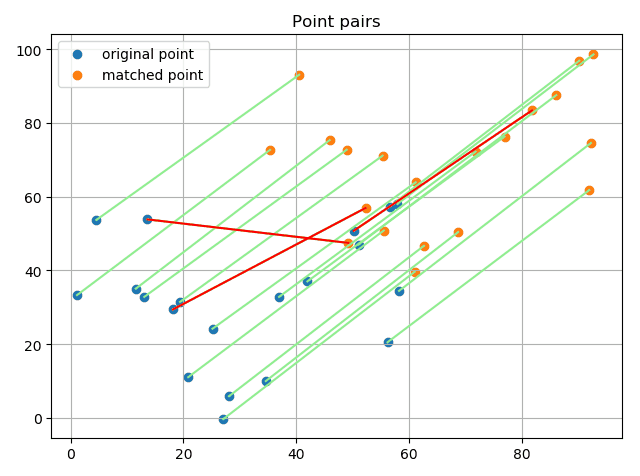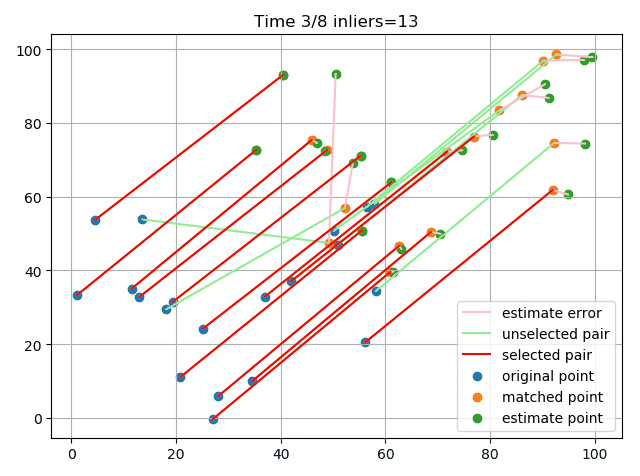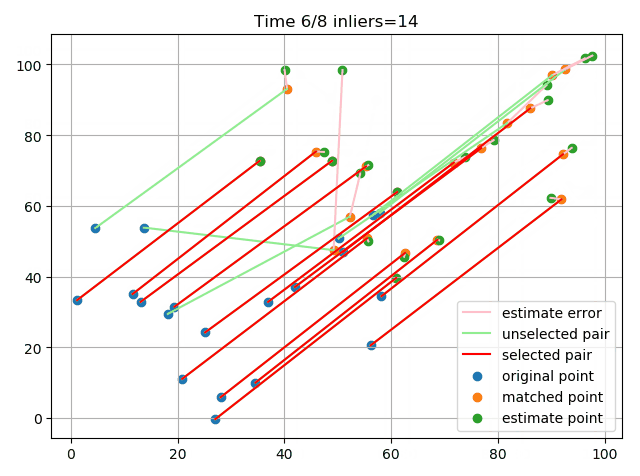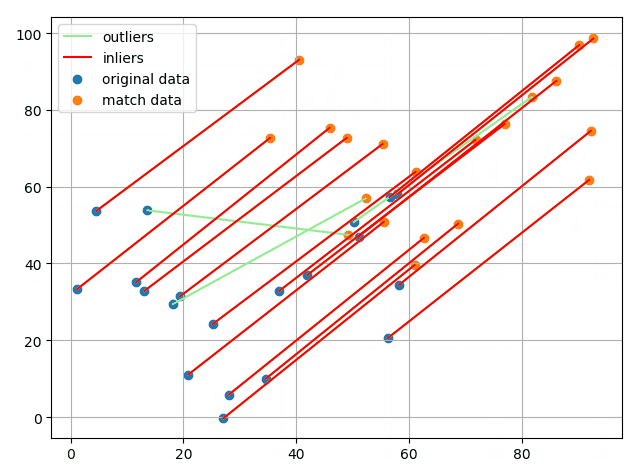
最后在实际的图片上提取特征点并进行匹配，利用RANSAC剔除离群点：

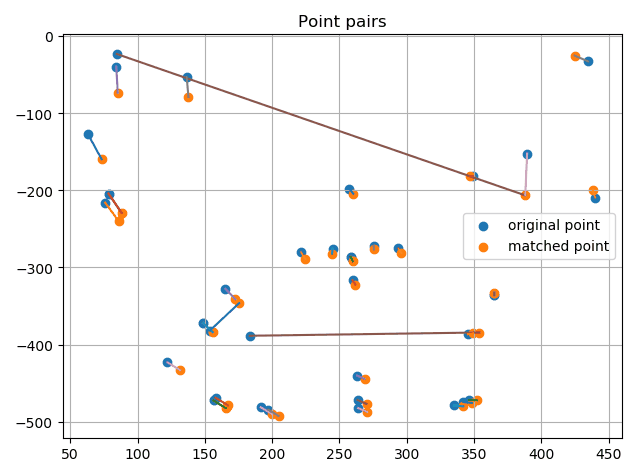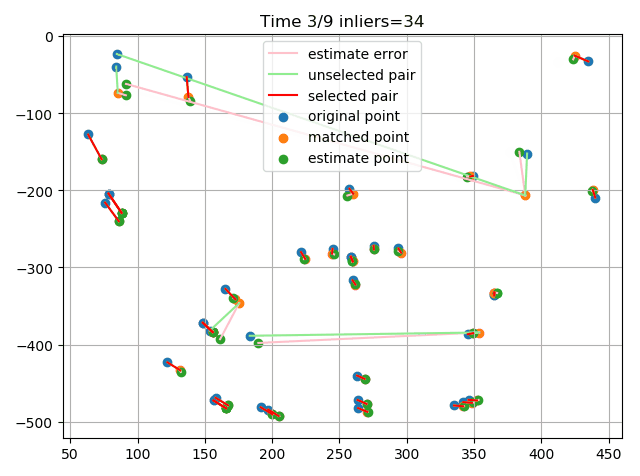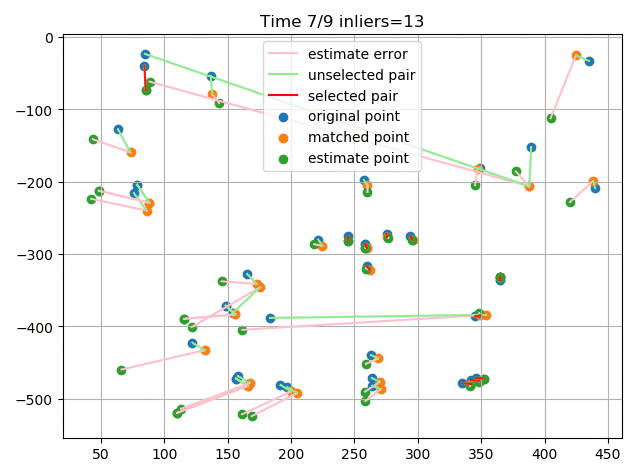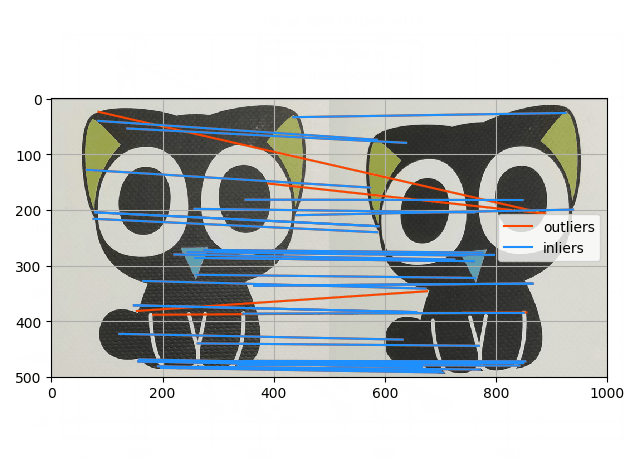
可以看到，总体效果还是不错的，成功识别出了一些错误的匹配点对。这里的误差度量用的是重投影误差，简单来说就是根据随机选择的4个点求解单应矩阵，然后利用单应矩阵对数据点进行变换，将结算出来的点与实际点计算欧氏距离，若其小于阈值则认为是内点。

四、小结

在两个不同的应用场景中可以看到由于模型以及评价指标的不同，导致在代码实现上存在差异。所以RANSAC在具体实现中并没有什么固定格式，需要根据当前数据以及模型不断修改调整。但相比于这些千变万化的实现，RANSAC的思想才是不会改变的本源，是需要我们记住的。